初中数学教学中数形结合思想的应用

吴 瑜

(浙江省温州市乐清市南塘镇中学 浙江 乐清 325600)

由初中数学知识可知，数形结合即：研究的对象为“数”与“形”这两种，并且二者之间有着密切的联系性。二者的结合，在解题过程中能够借助数学表达式去阐述图形的属性，还可以利用图形所给出的提示直观阐述出其数学表达式。从而将具有一定深度的“数”通过与图形结合的思想变得简单化，抽象问题直观化。[1]学生通过数形结合的方法在实际解题中处理了很多的数学难题的同时也给教师在数学教学过程中提供了便利。所以，学生务必学会灵活应用数形结合思想，高效处理所遇到的各种难题。

1.函数中数形结合思想运用策略

函数知识在初中数学知识中占有很大比例，对于刚接触的学生来讲有一定的理解难度，而且函数知识对学生有一定的基础能力要求和理解能力要求，才能进一步的掌握函数知识的核心。函数知识具有多样性的特点，并且具有一定难度，如若学生在解题的时未能真正理解出题人的用意，便会呈现出低质量的学习过程。所以，教师在数学教学过程中，要学会给学生灌输数形结合解题思想，帮助学生们理解解题思路，从而做到以“数”助“形”，或者以“形”助“数”。

举例：在浙教版中初二年级数学中的一次函数，一次函数y=kx+b的图像如图所示，当y<0时，x的取值范围是多少?

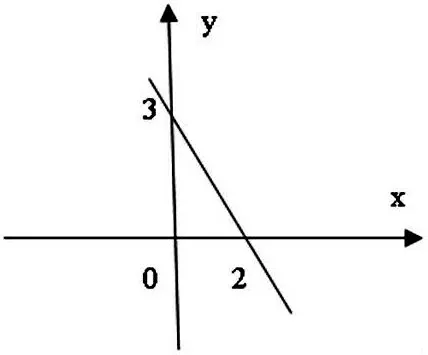
利用图形结合思想，由图形中给出的x轴上的(2,0)，y轴上的(0,3)两个坐标代入方程式中2k+b=0;b=3这两个式子可以得出k的取值为-3/2。同时我们还可以利用数形结合思想中的图来检验我们所取得的k值的正负性。由图可知图线呈下降趋势且经过第一、第二、第四象限，所以k的值一定为负数。也针对我们之前计算的k值做一个简单的判定。所以一次函数解析式为y=(-3/2)x+3，当Y<0时，由图形可知，即为x轴的下半部分，所对应到直线段上的部分为x>2，故，当y<0时，x>2。

利用数形结合的方法，能够很容易的使函数知识通过图形解题的方式变得简单易懂，同时也更好的将题目的关联性展示给学生们，使学生更透彻的掌握函数概念。

2.方程求解中数形结合思想运用策略

方程式初中数学内容中的重点同时也是难点且涉及面很广。因此，教师为了更好的让学生们可以对方程的有效认识，就需要借助数形结合的方法降低实际方程解决问题的难度[2]。简而言之，学生在遇到解答方程有关的数学问题时，可以运用图形的方式将问题简单化的表达出来，由此更加清晰、明了整个方程问题。

例如，小明和小红在同一时间点以家为起点，向公司出发，20min以后二人在超市集合，但这时小红忘记带开会用的u盘，需要重新回家拿，用时10min，这时小明发现忘记带笔记本也需要回家，其用了15min，请列出小明和小红两个人分别与时间的关系表达式。这时如果从正面直接回答问题可能会有一些难度，所以不妨借助数形结合的思想。

小明到公司的距离与时间的关系 小红到公司的距离与时间的关系

由图可以很清楚的观察小明和小红的距离与时间之间的关系，既将复杂问题通过数形结合的方法简单化，又对学生们的数学思维能力培育和综合能力的提高有很大的帮助。

3.三角函数中的数形结合思想运用策略

三角函数也是初中数学知识点中的较为重要的内容，它贯穿在整个初中数学，但是因为其具有较强的抽象性特点，就需要教师在进行数学教学过程中贯穿一定的教学策略使学生们更加容易理解，掌握三角函数知识。教师可以采用数形结合的思想作为解决三角函数的策略，既将问题简单化又一目了然，很大程度锻炼了学生们数学思维能力。

例如，学习三角函数《正弦与余弦》这一课时，教师可以在有条件下进行实际操作，可以让学生们拿出作图工具三角尺与量角器，学生可以用量角器画出两个30度的角，并且这两个三角形大小不同，采用量角器测量并且计算出30度角所对应的边、邻边、斜边的比值，接下来学生们观察通过计算所得到的结果。在数形结合的作用下，可以让学生对三角函数理解的更加透彻，提高课堂效率。

4.结束语

综上所述，初中数学对学生尤为重要，学会采用正确的方法解题至关重要，数形结合思想贯穿数学始末，它可以使一些复杂问题由此简单化并且更易理解。所以，教师在日常教学过程中渗透数形结合的思想，协助学生们掌握数形结合思想，锻炼学生们的数学思维和数学解题能力的同时也构建了数学高效课堂，为学生们创建了丰富多彩的教学内容，在一定程度上推动了初中数学教学的发展进程。