新型桥墩模型在钢筋混凝土桥梁结构中的应用研究

黄鹤，秦攀，黄汉义

(中交第二公路勘察设计研究院有限公司，湖北 武汉 430052)

抗震设计的本质思想是如何为结构提供抵抗地震作用的能力，中国是一个经常发生地震的国家，对于处于地震带中的桥梁工程，传统的设计理念一般采用增加上部结构强度的方式来满足抗震设计的要求，但是这种方式成本较高。

学术界对减隔震设计的研究起源于20世纪60年代，是由于人们发现很多没有约束的建筑结构在强烈的地震荷载作用下能够完好的保存下来，在此基础上减隔震设计开始引起了人们的重视，并且逐渐提出了一套完整的减隔震设计理念，主要包括两种不同的类型：一是桥梁上部结构与下部结构之间采用隔震支座的墩顶支承隔震技术; 另一种是自复位桥墩技术，主要是在墩与基础之间设置具有独立的耗能组件。在此基础上，国内外很多学者对其进行了研究，Yim，Shenton等对刚体的摇摆和滑动行为进行了大量研究，结果表明：结构的摇摆行为可以降低自身的地震响应；Housner在1963年率先进行了研究，并指出能够摇摆的结构可以消耗部分地震能量；2001年，Makris和Zhang通过大量试验针对约束刚体的摇摆响应进行了研究，结果表明：受约束的刚体比无约束刚体更能承受高振幅的摇摆，但是仅仅局限于一定的频率范围，当摇摆动作处于某种频率状态时，结果将是相反的。

目前，国内外常见的自复位装置主要包括加台两侧设置限位钢筋的自复位结构、墩身中心设置预应力防倾覆钢筋的自复位结构以及设置耗能阻尼器的自复位结构等形式的自复位装置。试验研究以及工程检验表明：此类型的构件减震效果并不明显，并且设计构造复杂，施工难度大，在实际应用中不太理想。因此，该文基于钢筋混凝土桥墩良好的抗震性能，提出一种新型的钢筋混凝土自复位桥墩模型，并对该模型的减隔震机理及效果进行研究。

1 工程背景

阅江大桥位于广东省肇庆市，项目线位起点位于北岸端州区古塔路与星湖大道交叉路口，沿古塔路跨越西江，在南岸高要乌榕村与世纪大道(S272)衔接。主线全长3.837 km，其中主线桥梁2 355 m/1 座(计入互通主线桥长)，于建设路设置匝道出入口1处，终点设置互通1 处。主线桥梁桥跨组合为：5×25 m+(31+2×35+31)m+2×4×25 m +3×25 m +4×25 m+(27+41+32)m 现浇连续箱梁+(45+2×70+45)m 连续刚构+2×45 m +3×45 m预应力T 梁+(160+320+160)m 斜拉桥+2×45 m 预应力T梁，终点侧引桥计入世纪大道互通主线桥中。主桥采用双塔单索面，墩、塔、梁固结的预应力混凝土斜拉桥，跨径为(160+320+160)m，主梁采用单箱五室箱形断面，主塔采用钢-混组合塔，主墩采用重力式桥墩；引桥上部结构采用连续刚构、连续箱梁、预制简支T 梁3种形式，为了提高该桥梁结构的抗震性能，该文对新型摇摆自复位桥墩模型进行研究。

2 新型摇摆自复位桥墩简介

根据自复位减隔震设计相关理念提出图1所示的自复位桥墩柱试验模型。与传统桥墩相比，试验模型通过增加一定刚度的弹簧[如图1(b)]以及高阻尼橡胶垫块[如图1(c)]将加台的提离高度进行了限位处理，从而使其与墩柱形成一个整体。

在正常地震荷载强度作用下，桥墩依靠上部结构自重来抵御墩底弯矩，此时墩柱不会发生提离，弹簧或高阻尼橡胶垫块处于自由状态，如图1(a)所示。

(a)未发生提离状态

但是当地震荷载的强度较大时，自复位桥墩发生提离摇摆，墩身以及上部结构自重可以提供一个恢复力，从而使得结构具有一定的自复位功能[图1(b)、(c)]。

与传统自复位墩相比，该文提出的新型摇摆自复位桥墩设计变化范围小，易于实现。墩身无需额外的阻尼装置，本身可用作摇摆式耗能装置，从而节约了抗震设计的成本，并且其具有更广泛的应用范围。

3 钢筋混凝土自复位桥墩模型研究

3.1 钢筋混凝土自复位桥墩模型设计

文中的原型墩是一个钢筋混凝土矩形墩，其主梁跨度为12 m。钢筋混凝土矩形墩是基于原型桥墩，采用结构相似性原理设计的。在模型上进行振动台试验，研究模型在不同地震波峰值加速度下的加速度和应力响应以及结构位移，最终根据试验结果选择出抗震性能较好的摇摆钢筋自复位桥墩试验模型，试验模型的具体尺寸如图2所示。

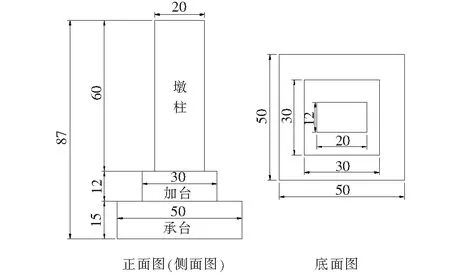
图2 试验模型尺寸图(单位：cm)

基于相似条件，试验模型均按照1∶20的比例设计了两种不同类型的钢筋自复位桥墩试验模型。自复位试验模型Ⅰ是在平台的两侧设置高阻尼橡胶垫块，如图3所示，高阻尼橡胶垫可以在桥墩发生提离后提供限位和复位功能，同时可以通过橡胶垫块消耗一部分震动能量，从而实现保护墩身的作用。

图3 试验模型Ⅰ：设置高阻尼橡胶支座的摇摆隔震桥墩

模型Ⅱ是在加台的两侧设置具有一定刚度的弹簧摇摆自复位桥墩试验模型，如图4所示，弹簧仅在墩被提离后提供限制和复位功能，弹簧本身不能够消耗地震能量。

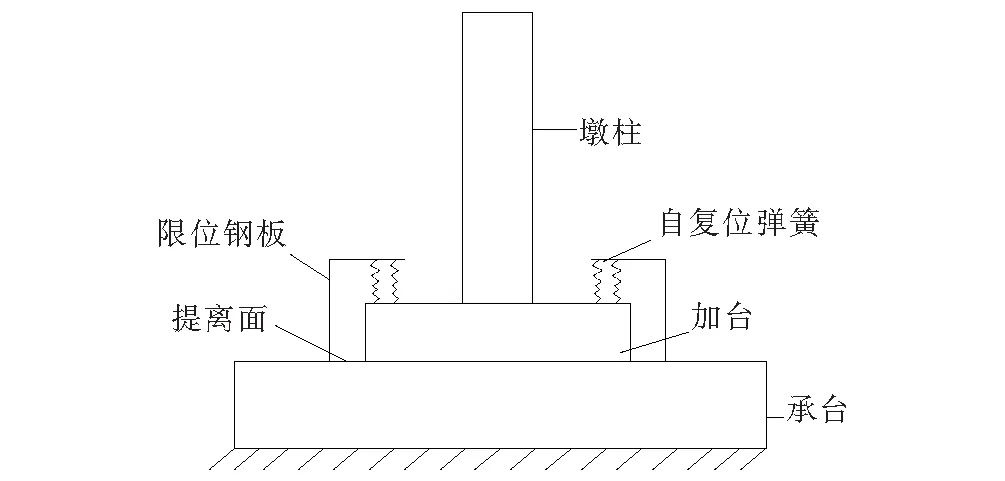
图4 试验模型Ⅱ：设置自复位弹簧的摇摆隔震桥墩

模型Ⅲ为墩身、加台和承台为一个整体的传统重力式桥墩模型，如图5所示，设置模型Ⅲ的主要目的是作为参考模型与试验模型进行对比分析。

图5 试验模型Ⅲ：相同尺寸大小的传统重力式桥墩

以上3个模型的混凝土强度以及墩身和加台的配筋形式基本相同，模型均采用了强度为C30的混凝土，墩身配置了6根纵向钢筋，配筋率为0.7%，加台配置了20根纵向钢筋，外围用钢筋作为箍筋进行包裹，模型墩身与加台设计配筋形式如图6所示。

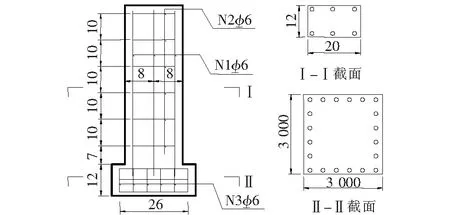
图6 试验模型墩身配筋图(单位：除钢筋直径为mm外，其余：cm)

试验模型中采用的钢筋材料性能如表1所示。

表1 钢筋的材料性能

3.2 模型测点布置

试验测试内容包括位移、加速度以及应变3项，在布置应变测点时主要考虑模型结构的地震反应，模型Ⅰ、Ⅱ测点的布置位置如图7所示。

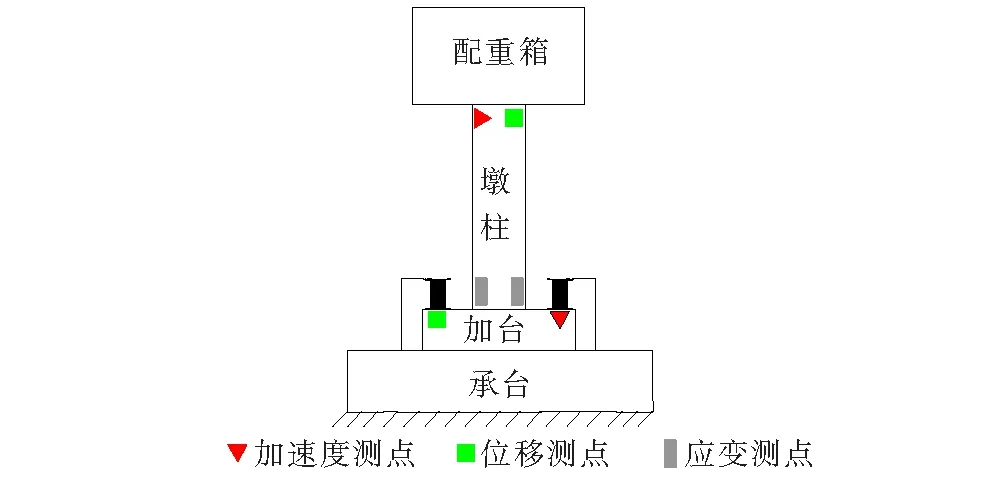
图7 测点布置图

模型Ⅲ没有布置竖向传感器，其余测点布置与模型Ⅰ、Ⅱ一致。

3.3 输入地震波

试验选取适用于Ⅰ类场地的EL-Centro地震波，在试验中将地震波加速度设置为0.2g(多遇地震)、0.4g(设计地震)、0.6g(罕遇地震)，试验过程从小到大依次进行加载，3种模型的工况保持一致，地震波的加速度时程曲线如图8所示。

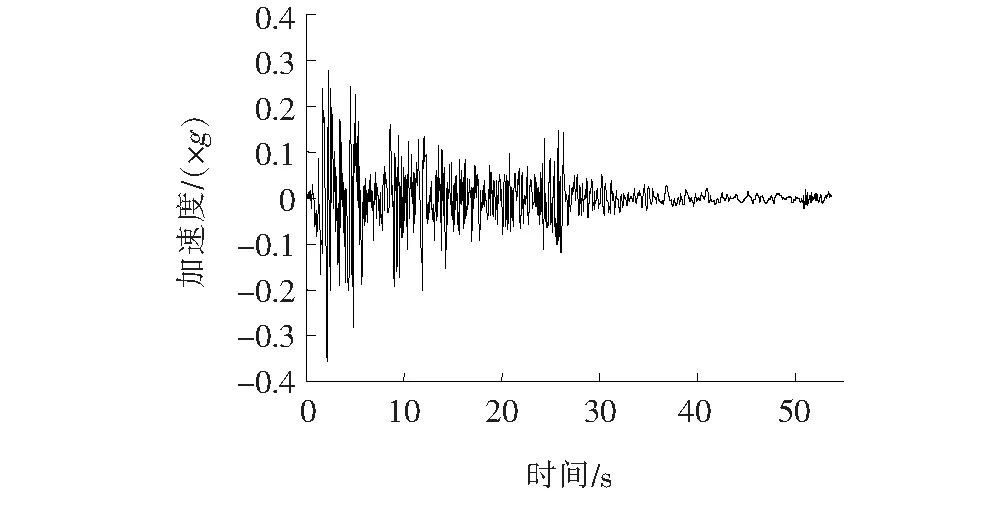
图8 试验加载的EL-Centrol地震波

4 模型结构的地震反应分析

4.1 试验现象

当输入地震波的峰值为0.2g时，模型Ⅰ、Ⅱ几乎不发生任何提离摇摆，这与模型Ⅲ的试验现象基本吻合；当输入地震波的峰值为0.4g时，模型Ⅰ、Ⅱ在地震作用下均发生轻微的提升摇摆; 当输入地震波的峰值为0.6g时，模型Ⅰ、Ⅱ产生大幅度的提升摇摆，在距离墩台底部5 cm处，模型Ⅲ的长边方向上产生裂缝，但是模型Ⅰ、Ⅱ在整个试验过程中均未发生明显的损坏。

4.2 加速度响应

3种钢筋自复位桥墩模型在0.2g、0.4g以及0.6g共3种不同峰值加速度的El-Centro地震波作用下，加台竖向提离加速度极值以及墩顶水平加速度极值如图9所示。

图9 不同地震峰值加速度作用下桥墩加速度极值

随着输入地震波峰值的增加，3种钢筋混凝土自复位桥墩模型墩顶的加速度极值不断增大。与传统桥墩模型Ⅲ相比，在0.6g地震波的作用下，模型Ⅰ对应的加速度极值减小了54%，而模型Ⅱ墩顶对应的加速度极值减少了78%。在0.6g地震波的作用下，模型Ⅱ的加台竖向提离加速度为模型Ⅰ的1.5倍，在三者中处于最大。

4.3 位移响应

3种钢筋自复位桥墩模型在3种不同峰值加速度的El-Centro地震波作用下，加台竖向提离位移极值以及墩顶水平位移极值分别如图10(a)、(b)所示。

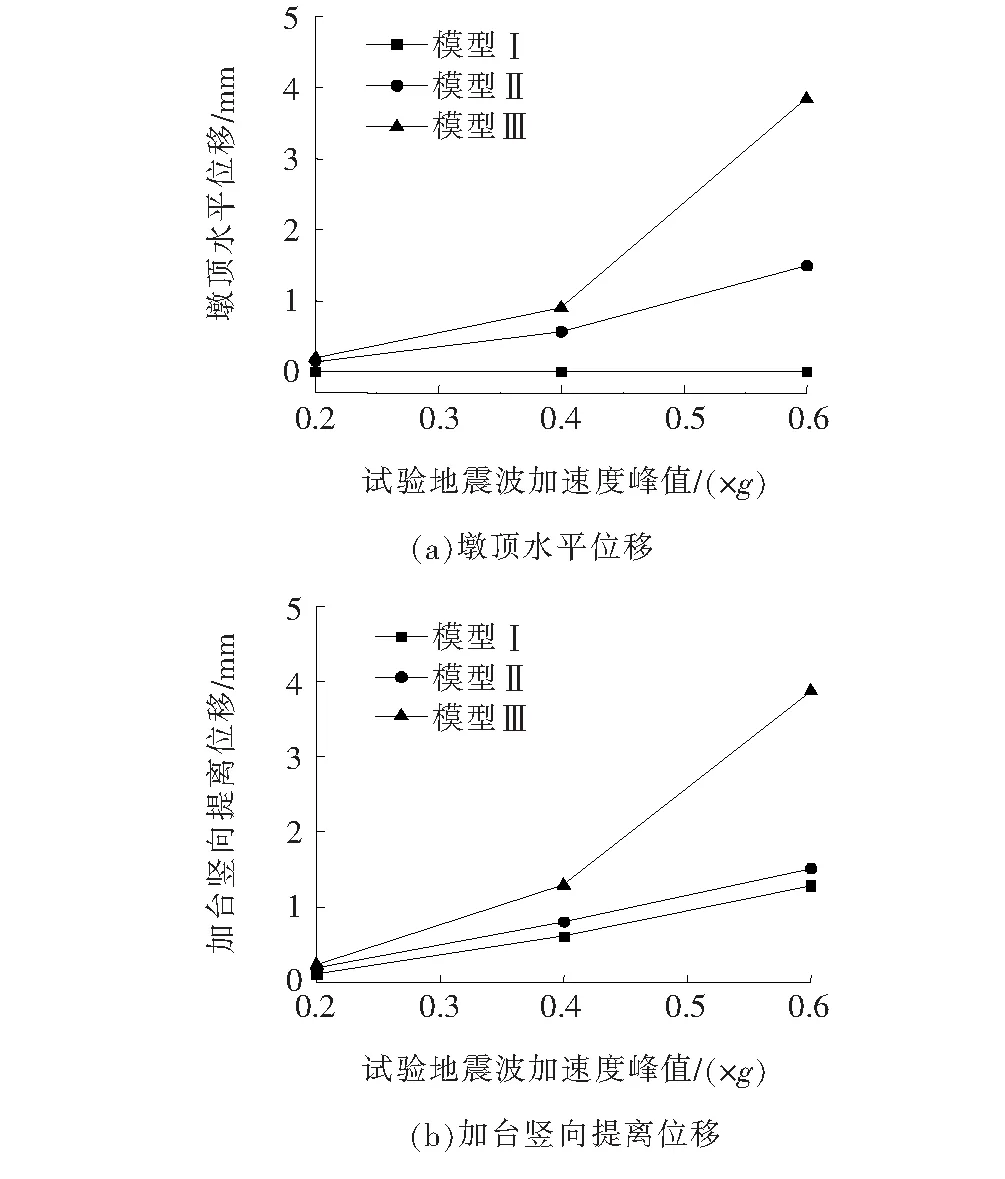
图10 不同地震峰值加速度作用下试验桥墩位移极值

3种钢筋自复位桥墩模型在0.6g的El-Centro地震波作用下，墩顶水平位移以及加台竖向提离位移时程曲线如图11(a)、(b)所示。

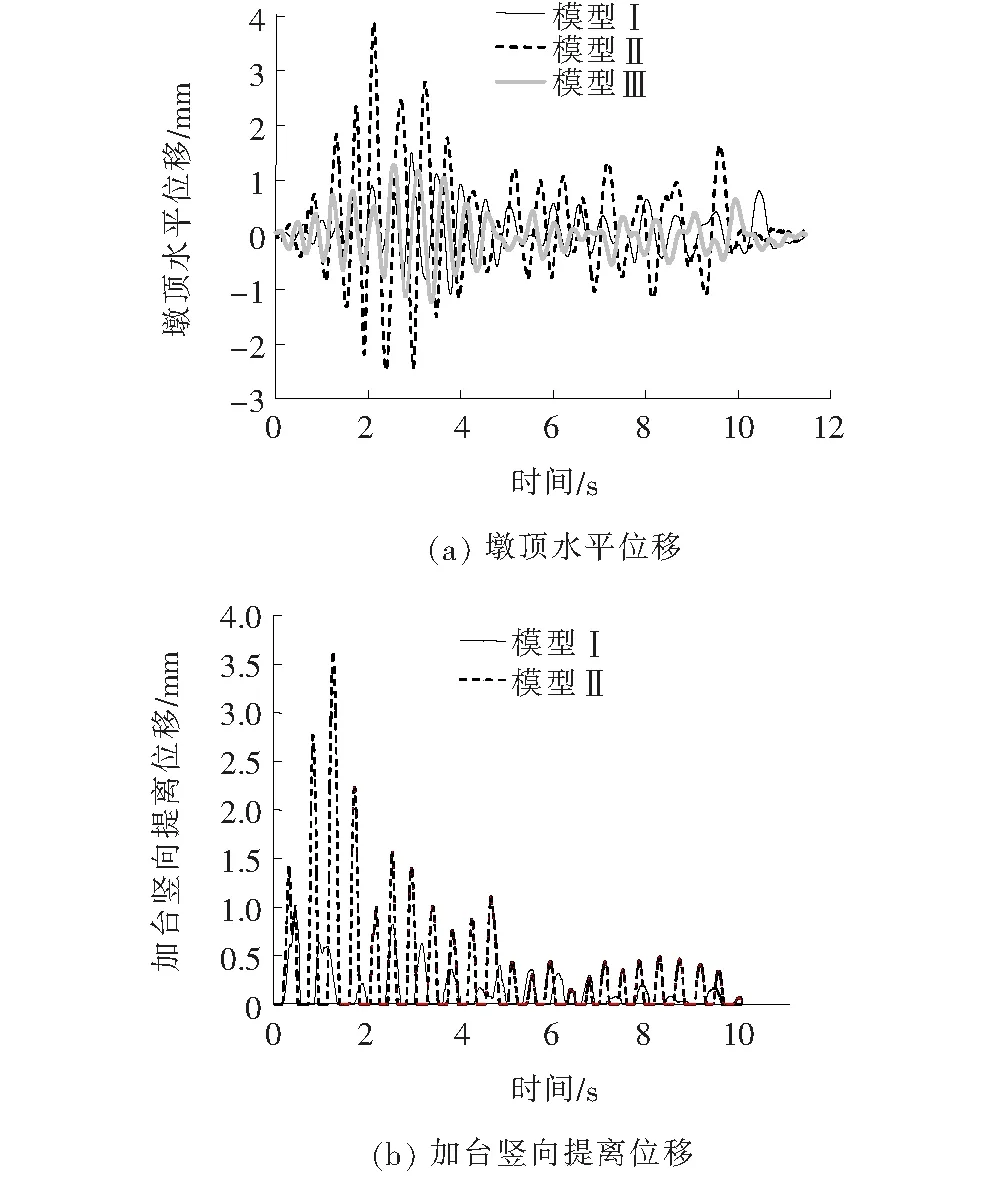
图11 3种试验模型墩位移时程曲线

由图10可以看出：随着输入的地震波峰值逐渐增大，3种钢筋自复位桥墩模型的墩顶位移都呈现增大的趋势。在同种强度的地震波峰值荷载下，模型Ⅱ的墩顶水平位移达到最大值，模型Ⅰ次之，而模型Ⅲ的最值为最小。

与传统重力式桥墩模型Ⅲ相比，在0.2g的地震波作用下，模型Ⅰ的墩顶水平位移极值增大了75%，模型Ⅱ极值增大了110%。但3种钢筋自复位桥墩模型的墩顶水平位移数值都比较小，这也证明了多遇地震作用对模型位移结果影响并不明显；0.6g的地震波作用下，与传统重力式桥墩模型Ⅲ相比，模型Ⅰ的墩顶水平位移极值增大了17%，模型Ⅱ的极值则增大了两倍。

4.4 应力响应

3种钢筋自复位桥墩模型在0.2g、0.4g以及0.6g共3种不同的地震波作用下，墩底实测应力极值如图12所示。

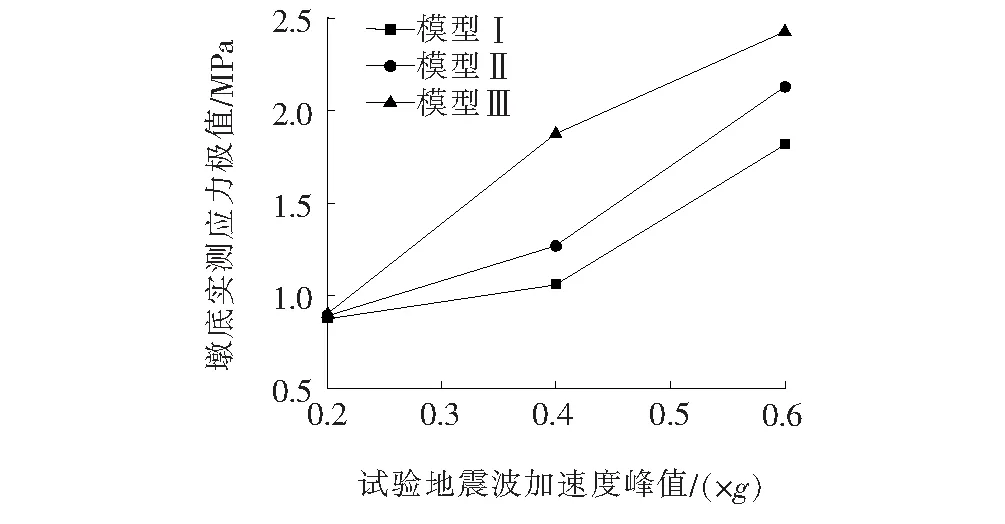
图12 不同加速度峰值作用下墩底应力极值

由图12可知：与传统重力式桥墩模型Ⅲ相比，在0.2g的地震波作用下，模型Ⅰ的墩底应力极值减小了0.9%，模型Ⅱ减小了2.7%，这也证明了多遇地震作用对模型墩底应力结果影响并不明显；0.6g的地震波作用下，与传统重力式桥墩模型Ⅲ相比，模型Ⅰ的墩底应力极值减小了12%，模型Ⅱ减小了25%，从而表明，新型摇摆自复位桥墩能够有效降低桥墩墩底应力值，有效避免桥墩在地震中受到破坏。

5 结论

通过对3种钢筋自复位桥墩模型进行试验研究，得到以下结论：

(1)与传统的重力式桥墩相比，在同种烈度的地震波作用下，新型钢筋自复位桥墩模型在应力响应以及加速度响应方面都有所降低，表明这两种自复位桥墩模型具有良好的减隔震性能。

(2)与传统的重力式桥墩相比，在同种烈度的地震波作用下，新型钢筋自复位桥墩模型在墩顶水平位移响应方面会有所增大，主要是由于墩顶与基础部分的约束比较薄弱，因此在摇摆隔震桥墩的设计中应对墩顶的水平位移重点关注。

(3)与设置自复位弹簧的钢筋摇摆自复位桥墩相比，设置高阻尼橡胶支座的自复位桥墩加速度以及应力响应更小，但位移响应相对较大，高阻尼橡胶支座的摇摆自复位桥墩是一种更为理想的摇摆自复位结构形式。