不同卸料流态对仓壁侧压力影响的试验研究
周长明 肖昭然 刘克瑾 魏世广 刘 勇 王世豪 张丰尧
(河南工业大学土木工程学院1,郑州 450001) (陆军工程大学2,南京 210042)
筒仓作为颗粒物质的存储容器,广泛应用于食品、化工、制药等工业工程领域[1]。筒仓卸料是仓储的重要环节,卸料过程中伴随着流态的变化,仓壁压力也会发生不同的变化,压力峰值甚至可以达到静态压力的数倍[2-5],使筒仓的不稳定性增加,可能会引起筒仓工程事故。因此,对筒仓卸料流态及仓壁压力进行研究具有重要的现实意义。
针对筒仓卸料过程中的流态及其仓壁压力分布规律,学者们进行了相关性研究。关于筒仓压力计算方法,刘定华等[6,7]、张家康等[8,9]从平衡条件和常系数假定出发建立微分方程,得出仓壁静态及动态压力的计算公式,并通过模型试验和数值计算,发现与理论计算值相接近。
筒仓的流动类型分为整体流、漏斗流、管状流及扩散状流动四种形式[6],杜明芳等[10]和甄浩淼等[11]指出一种流态伴随着另一种流态一同出现,且各种流态之间会发生转化,俞良群等[12]通过速度场分析发现整体流动区域和管状流动区不存在明显的分界线。针对各种流态的变化,Volpato[13]和Yang[14]等对筒仓内添加改流体,能够实现流态由中心流到整体流的转化,其峰值应力位置也会发生改变。同时,谭源强等[15]和肖国先等[16]对筒仓内添加改流体,能使仓壁应力峰值降低。
关于筒仓静态侧压力方面,韩阳[17]利用物理筒仓模型研究筒仓散装粮堆的边界压力分布规律,发现静态储粮状态下,当装粮高度大于筒仓直径时,仓壁侧压力开始逐渐小于Janssen公式计算结果。杨鸿[18]对贮料工况下不同物料进行参数分析发现,泊松比和内摩擦角的影响较大。
关于筒仓动态侧压力方面,陈长冰等[17]和肖昭然等[20]通过离散元模拟分析发现,仓壁最大动态压力值不是出现在卸料瞬间,而是在卸料一段时间以后。刘克瑾等[21]利用离散元软件与物理实验结合的方法,从细观颗粒层次探求引起仓壁压力增大的原因是拱的形成,同时动态成拱机制也是仓壁压力出现波动性变化的根本原因。
国内外学者通过理论计算、离散元和物理模型试验的方法,对筒仓静、动态侧压力及卸料流态的研究方面取得了丰硕的成果,但是,关于在卸料过程中物料内部的流态变化,以及不同的流态变化下的仓壁压力变化规律,仍需从试验的角度加以验证。
因此,本研究采用物理模型试验的方法,自主设计并定制了可以观察内部流态发展变化的半圆形有机玻璃试验筒仓,选用质地均匀的陶球颗粒为散体物料,设计制作固定尺寸、适宜量程、满足精度要求的土压力盒传感器来测取贮料和卸料过程中的仓壁压力数值,采用压实和松散两种装料方式,对物料不同内部流态下的仓壁压力变化进行试验研究, 观察筒仓内部的物料流态变化,分析不同流态下的仓壁压力波动性及超压变化规律,为筒仓贮料下的仓储结构及卸料过程的压力理论研究提供参考。
1 试验概况
1.1 模型设计
为了更好的观察筒仓内物料的流动状态,同时将流动状态实时地与侧压力进行联系,参考Fullard等[22]关于筒仓内部颗粒流速的模型试验以及Weinhart等[23]关于筒仓内部流态的离散元模拟研究,现采用有机玻璃设计制作了半圆形筒仓,可以清楚地观察到贮料在仓体内部的流动情况。筒仓直径0.5 m,卸料口直径0.05 m,壁厚0.01 m,仓高1.1 m,标记有1 m的刻度,便于观察和测量装粮及卸粮高度。考虑到模型筒仓离地面有一个高度方便卸料,以及便于与地面固定,模拟筒仓基础,设置钢材支架支撑模型筒仓。模型半圆形筒仓及详细尺寸标注如图1所示。

1.2 试验仪器及物料性质
试验中用压力传感器直接测取半圆形筒仓仓壁的动态侧压力,半圆形筒仓截面仓壁上的实心圆形即为压力传感器的所在位置,布设C1~C7共7个压力传感器,7个压力传感器在一条直线上,所成直线与仓底直径角度为45°。压力传感器采用内嵌式固定在筒仓侧壁上,其承压面与模型筒仓内壁齐平,参考文献[24]中为降低因贮料与仓壁的温度不同可能引起传感器有较大的温度输出,在传感器表面贴上一层塑料膜作为隔热层。所使用的传感器型号为丹东DYB-2,直径30 mm,厚度13 mm,量程50 kPa,分辨率5 Pa。采用DHDAS-3816动态信号采集分析系统进行数据的采集与分析,试验过程中,每隔1 s记录一次数据。
参考许启铿等[25]关于粮食力学参数的试验研究,选用内摩擦角与粮食颗粒相近,颗粒直径较小,硬度较大,能够重复利用的煅烧陶球作为研究对象,陶球的具体物理参数如表1所示。

表1 煅烧陶球物理参数
1.3 试验内容及方案
试验通过两种不同的装料方式:压实落雨法装料和松散中心装料,分别简称为压实装料和松散装料。由于试验过程会受到填料方式、仓体变形、填料时内置传感器偏移等客观因素的影响,因此,两种装料方式均进行5次平行试验。每次试验的装料高度均为1 m,两种装料方式下最终分别装料约120 kg和110 kg。
装料完毕,待颗粒密实后,采集各测点贮料状态压力值,数据稳定后,快速抽出挡料板,在重力作用下自由卸料,整个卸料过程中用数据采集仪实时采集仓壁压力数据,用摄影机记录物料流动情况。
2 卸料过程流态的观察与分析
为更好反映和对比整个卸料过程中两种装料方式下流态的不同变化,特将卸料初始状态及卸料至1%、20%、40%、60%、80%、100%,共七个时期的流态图。
2.1 压实装料
压实装料下的物料流态如图2所示。
卸料前,整个筒仓内的颗粒间紧密接触。卸料开始瞬间,卸料口附近的颗粒快速地流出,在卸料口正上方出现一个管状的流道,流道宽度上下一致,约12 cm,卸料口正上方物料表面即出现漏斗。随着卸料的继续进行,流道逐渐变宽,逐渐演变为上方圆柱状、下方漏斗状,整个卸料过程,流道边界均未到达筒仓壁。整个卸料过程表现为管状流态。
2.2 松散装料
松散装料下的物料流态如图3所示。
卸料前,整个筒仓内的颗粒间紧密接触。
卸料开始瞬间,卸料口附近的颗粒快速地流出,卸料口上方颗粒不断地向下流动。距离仓底30 cm及以上颗粒沿着仓壁缓慢向下移动,各点颗粒流动速度基本一致,处于整体流动,物料的水平截面保持水平;而距离仓底30 cm及以下部分,以卸料口正上方位置的物料流动为主,仓壁处,测点C6附近及以上位置颗粒流动缓慢,处于漏斗状的流动状态。该卸料阶段表现为整体流与漏斗流共存阶段。该试验流态与俞良群[12]所观察到的试验结果一致。
随着卸料过程的进行,卸料口正上方位置颗粒继续保持高速流动,在仓壁处,具有缓慢流速的区域从测点C6位置不断向上延伸。至卸料40%,整个物料区域转变成漏斗状流态,中心流动区域水平宽度变宽,卸料口正上方物料表面开始出现漏斗,仓壁附近的颗粒停止竖向移动,不断地流进漏斗,沿着中间流道流出卸料口。卸料口正上方物料颗粒继续竖向匀速向下流动。测点C3-C5高度位置为过渡区域。该卸料阶段表现为整体流向漏斗流过渡阶段。

图2 压实装料下卸料流态图

图3 松散装料下卸料流态图
随后,卸料口正上方物料表面形成漏斗的曲率不断增大,整个物料区域继续保持漏斗状流动状态。至卸料完毕,整个物料区域靠近仓壁的颗粒不再移动,卸料口正上方颗粒逐渐形成漏斗状空间,直至漏斗状底部接触卸料口位置,卸料停止。整个卸料过程结束后,由于陶球自身的内摩擦力作用而在仓内存在如图3中卸料100%时期的流动死区,剩余物料最大堆积高度为11.25 mm。该卸料阶段表现为漏斗流阶段。
两种装料方式在整个卸料过程中,卸料前,颗粒密实度高,卸料瞬间,颗粒间密实度降低的区域由卸料口不断向物料表面延伸,随后的卸料过程,除流动死区外,其余物料区域都保持着低密实度的状态。同时在整个卸料过程中,卸料口正上方物料区域都保持着较大的流动速度,仓壁位置流速较低。同一水平面上的颗粒,卸料口正上方的颗粒先流出。
3 仓壁压力测试结果与分析
本研究给出的贮料工况及卸料工况压力为5次试验数据的代表值,试验数据采用统计方法分析和处理。
3.1 贮料工况
两种装料方式下,装料完毕后,贮料状态的压力值与Janssen公式计算值的具体数值如图4所示。

图4 贮料工况压力值与Janssen公式计算值
由图4可见,三组数值变化趋势大致相同,其中松散装料比压实装料时压力值大,且在筒仓下部分更为明显,这是由于压实装料时颗粒密实度更大,内部具有更密集的力链网络[26],颗粒的重力更多的是由内部的力链网络来承担,因此,传递到筒仓仓壁上的应力较小,且压实装料时的各测点压力值均分布在Janssen理论计算值左右,说明该试验结论基本符合客观事实。同时,在松散装料时,随深度的增加,试验值与计算值的差值增大,这一研究结果与刘定华、杨鸿和Fullard等[6,18,22]所得结果相同。因此,在《钢筋混凝土筒仓设计规范》(GB50077—2003)中都会在计算仓壁侧压力时乘以深仓储料水平压力修正系数。
3.2 卸料工况
物料颗粒在自重作用下流出卸料口, 将两种装料方式下各测点的变化曲线绘制如下图5所示:
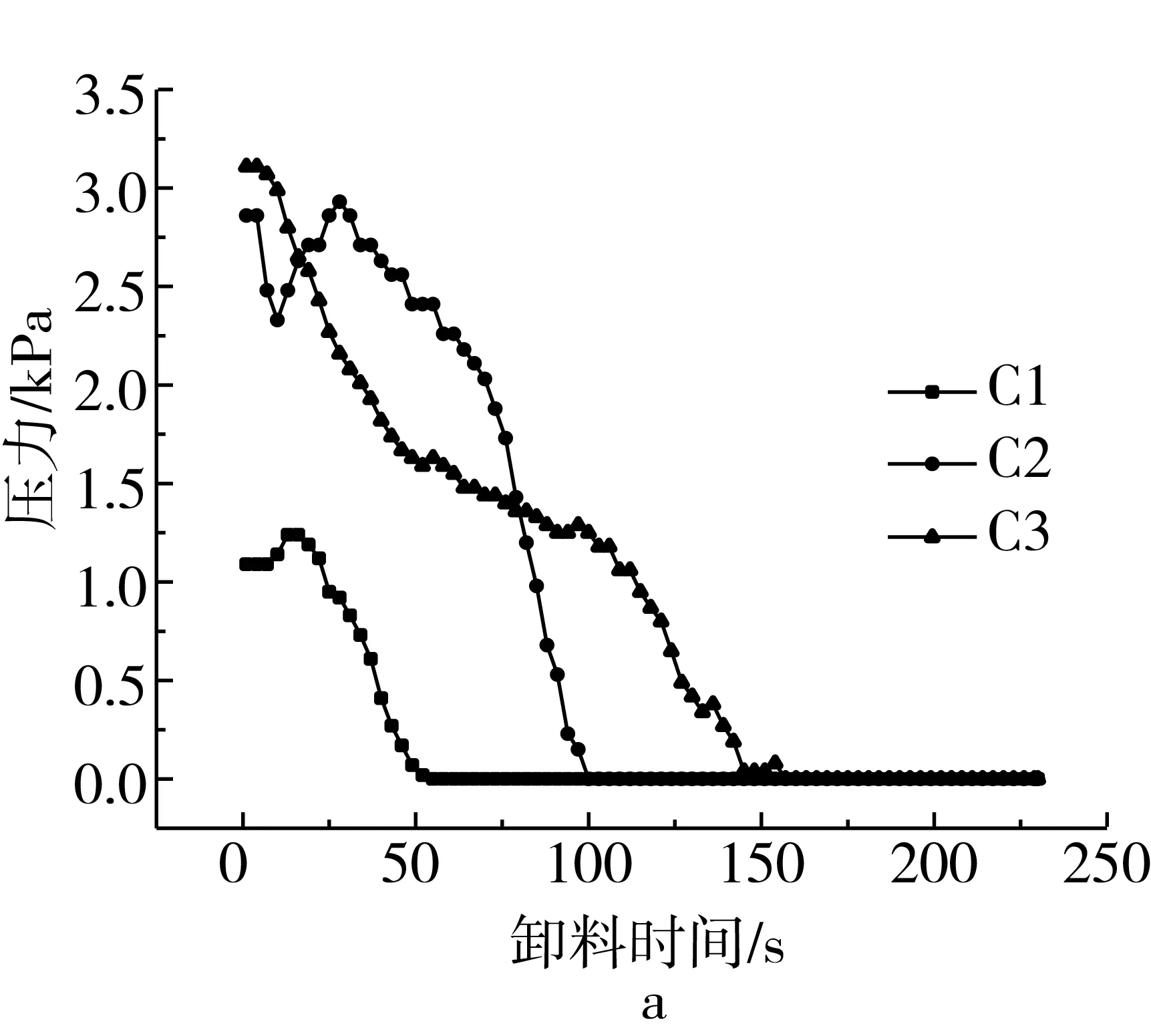
由上图可见,靠近仓壁顶部越近的测点,侧压力数值趋于零的试验越早,因此曲线总体变化趋势是合理的。松散装料时,在卸料瞬间,测点C2、C3、C7位置压力数值明显增大,测点C4、C5位置明显减小,这是由于卸料口打开后,筒仓贮料由仓底向外流出,各个颗粒在较短的时间内完成了由静止状态向运动状态的转变,颗粒间发生相互碰撞和挤压,直接导致仓壁压力增大,而测点C4、C5处在卸料前有较大的物料密实度,在卸料瞬间,测点以下位置的物料快速流出,密实度减小,因此,该处压力数值瞬间减小,在测点C7处为流动死区,颗粒流速为零,具有较密集的力链网络[27],加上卸料死区所在区域斜面会受到上部流动荷载的压力冲量,并将压力荷载传递至仓壁,因此表现为压力数值增大。压实装料时,在卸料瞬间,各测点压力数值无明显的增大或较小现象。
在卸料过程中,松散装料时,测点C2、C3处表现出较大的波动性变化,该区域为整体流区域,测点C4~C5出为漏斗流区域,表现出较小的波动性变化,压实装料时,整个卸料期间,各测点压力数值无较大的波动性变化。
对比两种装料方式,各测点在卸料瞬间及卸料期间的压力数值变化规律分析可见,压实装料下,筒仓具有更好的整体稳定性,同时,管状流为筒仓卸料设计的首选流态。
3.3 超压分析
参考国家规范《粮食钢板筒仓设计规范》(GB50322—2011)第4.2.3条,定义动态压力修正系数为卸料中动态仓壁压力与静态仓壁压力之比,下图给出了两种装料方式下动态压力修正系数随深度的分布图,如图6所示:

图6 动态压力修正系数
由图6可见,压实装料时,动态压力系数均为1左右,无明显的超压现象。松散装料时,在测点C2、C3、C7处有明显的超压现象,其中在测点C2处具有最大的超压系数1.85。说明整体流时超压现象比管状流时及漏斗流时超压明显,且整体流时波动性最大点与具有超压系数最大点一致。
4 结论
本研究通过自主设计并制作半圆形筒仓,采用两种不同的装料方式,观察不同的卸料流态,并对贮料工况压力及卸料过程中物料流态和仓壁压力的联合分析,得出如下结论:
筒仓卸料时的流动状态与物料的密实度有关,当物料密实度较大时,表现为管状流,当密实度较小时,表现为整体流与漏斗流。
当物料密实度较大时,仓壁压力数值与Janssen公式计算值较为一致,当物料密实度较小时,仓壁压力数值比Janssen公式计算值大,这与物料内部的力链网络的密集程度有关,因此,在GB 50077—2003《钢筋混凝土筒仓设计规范》中要求在计算仓壁侧压力时乘以深仓储料水平压力修正系数。
筒仓卸料过程会出现管状流、整体流与漏斗流三种物料流态形式,不同的流态会有不同的仓壁压力变化,其中压力波动性变化按照从大到小的顺序排列为:整体流区域>漏斗流区域>管状流。同时,整体流区域更易产生超压变化,在仓壁波动性最大测点位置具有最大的动态压力修正系数。

