爆破地震波传播规律数值模拟分析
孟庆浩,欧阳天云,李爱陈
(保利新联爆破工程集团有限公司,贵州 贵阳550002)
我国赋存的露天矿产资源非常丰富,开采总量也逐年上升,露天矿产资源开采最直接、最简单、最有效的方式便是爆破开挖。随着爆破开采规模的逐步扩大以及开采深度的不断加深,开采过程中形成了大量的露天岩质边坡,受地质构造、岩体结构类型、地层岩性、地形地貌、天然地下水等多方面因素的影响,边坡的稳定性受到影响。同时,爆破开采过程中产生的爆破地震波[1-5]也加重了边坡的不稳定性,尤其对邻近边坡的影响更为严重。 其影响体现在2 个方面[6-7]:①爆破荷载反复作用不同程度的多次削弱边坡抗剪强度,不断降低边坡稳定性系数;②爆破地震产生的惯性力尤其径向惯性力致使边坡下滑力增加,导致边坡失稳性趋强[8]。
研究爆破荷载作用下边坡的动力响应特征,对防止边坡失稳具有重要的意义。
1 岩石的物理力学参数试验
为了提高岩石物理力学参数试验的准确性,主要针对振动试验边坡岩体的力学条件进行着重研究,标准试样取自同一砂岩岩块,并做好标记。
根据岩石力学室内试验规程要求,将岩石单轴抗压试验试件制备成标准圆柱体。对岩石抗拉强度的试件,按照要求采用直径为50 mm,高为25~50 mm(高度为直径的0.5~1.0 倍)的标准圆盘。经过磨石机磨平后使试件达到试验要求,并在制样过程中剔除已发生变形破坏和不规整、不符合要求的岩样。
对砂岩试件进行抗压、抗拉变形试验后,试件的破坏形态主要以2 种形态呈现,即剪切破坏和柱状劈裂破坏。通过现场地质调查,并借助现有的地质勘测资料取样进行室内岩石物理力学参数试验,采用单轴压缩试验,抗拉试验得出砂岩的破坏特征:砂岩在发生破坏前没有明显的变形,达到破坏荷载时突然破坏,破坏后,变形和位移属于永久位移和永久变形。砂岩物理力学参数如下:密度2.5 t/m3;黏聚力0.32 MPa;内摩擦角30°;抗压强度43.5 MPa;抗拉强度6.5 MPa;弹性模量34.8 GPa;泊松比0.23;切线模量0.43 GPa;屈服应力35 MPa。
2 计算模型及数值模拟结果
2.1 材料模型与参数
1)边坡岩体本构模型。本次模拟采用了与应变率相关的塑性随动模型*MAT_PLASTIC_KINEMATIC 来模拟岩石材料,此材料模型不仅可以很好的表现岩体塑性、剪胀性等特征,适用于破坏后的岩体,还可以通过调整硬化参数来选择各向同性或随动硬化[9-11]。应变率可以用Cowper-Symonds 模型来考虑。台阶边坡岩体参数通过现场地质调查与室内岩石物理力学试验获得,台阶边坡岩体参数如下:密度2.5 t/m3;弹性模量34.8 GPa;泊松比0.23;切线模量0.43 GPa;屈服应力35 MPa。
2)炸药材料参数及其状态方程。炸药密度1 100 kg/m3,爆速为4 100 m/s,炸药起爆后,爆轰波产生拉应力使岩石破碎,爆轰产物的压力-体积关系用JWL状态方程来确定。
2.2 模型及边界条件
根据现场实际爆破情况建立模型。现场台阶要素与爆破参数为:台阶高度12 m、台阶坡面倾角75 °、炮孔直径120 mm、孔距5.5 m、排距4 m、超深1.2 m、装药长度9.5 m、填塞长度3.7 m;炮孔布置形式:垂直孔,每排5 个孔,4 排共20 个孔;采用孔间、排间微差爆破,孔间延时25 ms,排间延时50 ms。
为了简化计算,选取了5 个台阶边坡为研究对象。第1 台阶宽36 m,布置4 排炮孔,孔距5.5 m、排距4 m,最后1 排孔距第2 个台阶坡脚线20 m;第2个台阶宽40 m;第3 个台阶宽30 m;第4 个台阶宽20 m;第5 个台阶宽20 m;台阶坡面倾角75°。
采用数值模拟软件,建立1/2 对称边坡爆破模型,在对称面上施加垂直约束,模型两侧面和底面施加无反射边界体条件以模拟无限介质,其他定义为自由边界[9-10]。建模时采用的是Solid-164 单元和流固耦合算法,采用六面体网格对模型进行网格划分。边坡几何模型示意图如图1。
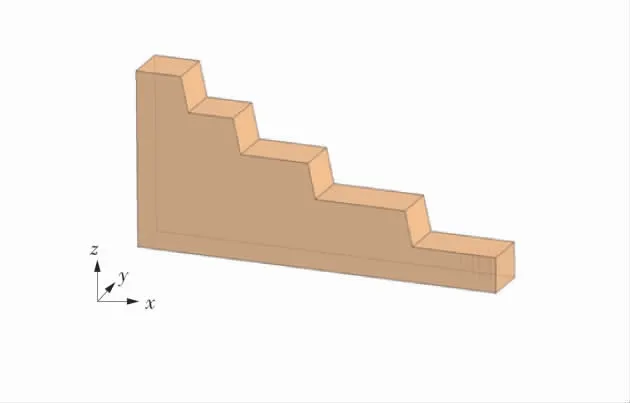
图1 边坡几何模型示意图
2.3 模拟过程及结果
以爆源上部和水平岩体为研究对象,分析振动波在岩体介质中的传播衰减规律。由于受到最大单响药量、爆心距、地质条件以及人为干扰等众多因素的影响,每次测试的爆破振动强度都存在差异。因此,根据每次爆破最大单响药量的不同,选取了前3 次爆破对露天矿边坡的影响,分别建立3 组模型进行数值模拟分析。根据现场每组设定的4 个测点,对应设置模型的4 个测点,模拟爆破后提取这4 个测点的振动速度时程曲线图进行分析。
以第1 次爆破振动数值模拟分析为例,模拟爆破最大单响药量81 kg,测点选取A、B、C、D,模拟爆破结束后提取这4 个测点的振动速度在三轴方向的速度峰值。模型测点对应位置布置示意图如图2,爆破振动传播至4 个测点时,台阶边坡振动速度云图如图3。
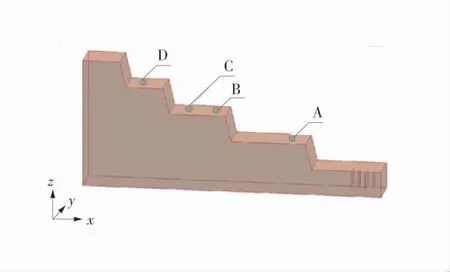
图2 模型测点对应位置布置示意图
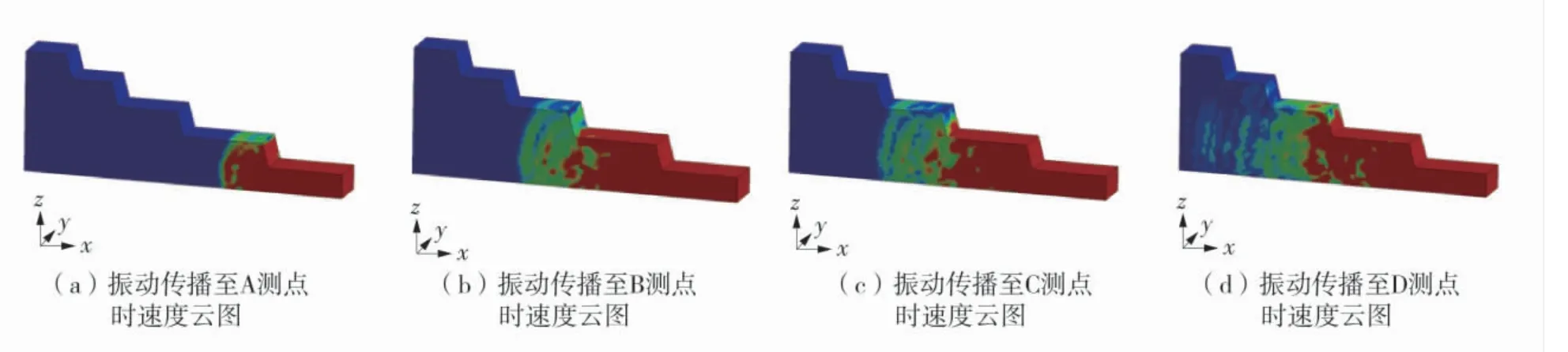
图3 台阶边坡振动速度云图
由数值模拟结果得出,测点A 的水平径向最大振动速度为3.11 cm/s,水平切向最大振动速度为2.95 cm/s,垂直方向最大振动速度为2.85 cm/s;测点B 的水平径向最大振动速度为1.84 cm/s,水平切向最大振动速度为1.92 cm/s,垂直方向最大振动速度为1.07 cm/s;测点C 的水平径向最大振动速度为1.46 cm/s,水平切向最大振动速度为1.38 cm/s,垂直方向最大振动速度为0.82 cm/s;测点D的水平径向最大振动速度为0.81 cm/s,水平切向最大振动速度为2.11 cm/s,垂直方向最大振动速度为0.86 cm/s。各测点x 轴的振动时程曲线如图4。采用同样的方式对第2 次、第3 次的模拟爆破进行建模分析,得出各个测点振动速度峰值。实测数据与爆破模拟的峰值速度及误差率对比见表1。

图4 各测点x 轴的振动时程曲线

表1 实测数据与爆破模拟的峰值速度及误差率对比
由表1 可知,3 次数值计算结果与实测结果大致相近,除去个别较大数据外,整体误差范围在20 %以内,由于模拟过程存在各种假设、简化以及忽略了节理裂隙等细节,使得计算结果与实测结果存在一定差异;3 次对比误差分别在10 %、15 %、20 %范围以内,由于矿山爆破是一个持续的过程,在进行数值模拟时未考虑前一次爆破对后一次爆破的影响,忽略了爆破损伤对岩体原有构造的破坏,导致后面爆破数值计算误差较前面误差大。
3 结 语
1)结合现有地质勘测资料,通过矿区现场实地取样、制备标准试样以及室内静力力学试验等一系列工作,获取了边坡岩体相关力学参数,为后续边坡数值模拟计算打下基础。
2)利用有限元分析软件对边坡爆破振动进行数值模拟与分析,得到炸药在边坡岩体中爆破后100 ms 内边坡测点速度时程曲线,探究了爆破地震波在边坡岩体中的传播衰减规律。
3)数值计算结果与实测结果对比,发现4 个测点振动速度数据与实际监测数据相近,其误差可控制在15%以内,验证了数值模拟用来预测爆破地震波的可行性。

