Major Development Under Gaussian Filtering Since Unscented Kalman Filter

Abhinoy Kumar Singh, Member, IEEE

Abstract—Filtering is a recursive estimation of hidden states of a dynamic system from noisy measurements. Such problems appear in several branches of science and technology, ranging from target tracking to biomedical monitoring. A commonly practiced approach of filtering with nonlinear systems is Gaussian filtering. The early Gaussian filters used a derivative-based implementation, and suffered from several drawbacks, such as the smoothness requirements of system models and poor stability.A derivative-free numerical approximation-based Gaussian filter,named the unscented Kalman filter (UKF), was introduced in the nineties, which offered several advantages over the derivativebased Gaussian filters. Since the proposition of UKF, derivativefree Gaussian filtering has been a highly active research area.This paper reviews significant developments made under Gaussian filtering since the proposition of UKF. The review is particularly focused on three categories of developments: i)advancing the numerical approximation methods; ii) modifying the conventional Gaussian approach to further improve the filtering performance; and iii) constrained filtering to address the problem of discrete-time formulation of process dynamics. This review highlights the computational aspect of recent developments in all three categories. The performance of various filters are analyzed by simulating them with real-life target tracking problems.

I. Introduction

THE modern era of science and technology has witnessed huge applications requiring state estimations from noisy measurements, e.g., target tracking, stochastic modeling,industrial diagnosis, and prognosis etc. [1]. Thanks to the filtering algorithms [1]–[5], which offer an efficient recursive state estimation tool. Filtering algorithms have helped in the modernization of several domains, such as space technology[1], medical [6], finance and economics [7], weather monitoring [8], etc.

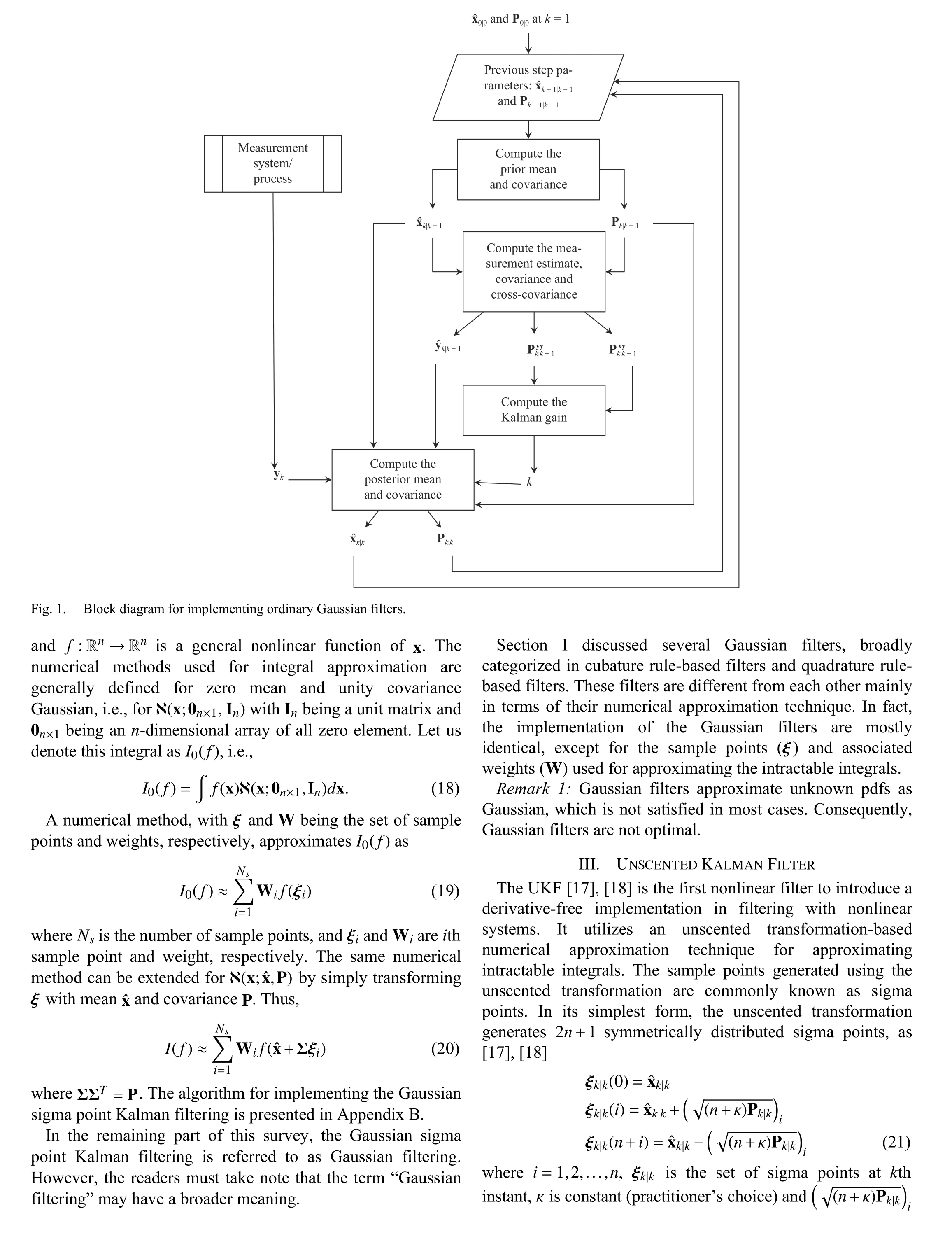
The Bayesian framework [9], [10] is a common choice among the practitioners dealing with real-life estimation and filtering problems. It gives a probabilistic estimate of states by formulating prior and posterior probability density functions(pdf) [9], [10]. An analytical simplification is perceived by analyzing these pdfs numerically, and the Gaussian filters [1],[10] are most popular in this practice because of their high estimation accuracy at low computational cost. The Gaussian filters approximate the pdfs (prior and posterior) as Gaussian,and characterize them with mean and covariance.

Researchers and industrial practitioners engaged with estimation applications would be grateful to Rudolph E.Kalman, who developed an optimal state estimation and filtering technique [11] for linear systems with white Gaussian noises. In the filtering literature, this technique is popularly known as Kalman filter [1]–[4]. The Kalman filter can be implemented with several linearly approximated filtering problems in different domains, like in target tracking [12] and communication systems [13]. However, the linearity constraint restricts its application with many more practical problems, where the linear approximation gives a poor characterization of system dynamics. A nonlinear filter,named as extended Kalman filter (EKF) [1], [3], was developed in the latter half of the sixties. It introduced a derivative-based local linearization of system dynamics, and propagated the mean and covariance through the locally linearized system models. It was further modified to improve the filtering performance by introducing several variants[14]–[16]. However, the derivative-based local linearization introduces many disadvantages to the EKF and its variants,like the smoothness requirement for systems model, poor estimation accuracy, and low convergence rate [1]–[3].Despite all these drawbacks, the EKF and its variants were the only alternative for more than three decades.

A derivative-free filtering method was introduced in the nineties, which is known as the unscented Kalman filter(UKF) [17]–[20]. The UKF approximates the desired pdfs as Gaussian, and characterizes them with mean and covariance.Although the Gaussian approximation of unknown pdfs encounters an error, it is more accurate compared to the EKF[17]–[20]. Furthermore, the mean and covariance are obtained from the first and second moments. The moment computation encounters an integral of the form “nonlinear function ×Gaussian distribution.” Such integrals are generally intractable, and approximated with numerical methods. These methods approximate the integrals up to a particular order of Taylor series expansion. Thus, the moment of higher-order terms is another source of approximation error or the estimation error. Full expression of mean in terms of higherorder moments is derived in Appendix A. Nevertheless, it finds other sources of errors, such as noise Gaussian approximation and discrete-time formulation of process models, which appear for the EKF as well.

The UKF implements an unscented transformation-based numerical method of integral solving. Using the same numerical method, many variants of UKF [21]–[27] appear in the literature. The derivative-free filtering approach of UKF offers several advantages, such as better stability and improved estimation accuracy. Subsequently, the research continued further, and several derivative-free filtering methods were developed to further improve the performance.The aforementioned Gaussian filtering is a popular class of numerical approximation-based derivative-free filtering methods (particle filtering is another popular class of derivative-free filters; however, this review is particularly focused on the Gaussian filters).

The Gaussian filtering literature after the development of UKF can be classified in three categories: i) advancing numerical approximation accuracy; ii) modifying the Gaussian filtering approach against several limitations; and iii)removing the constraints on conventional Bayesian framework. This paper reviews the computational aspects of significant developments in all three categories.

In the first category, the numerical approximation accuracy of intractable integrals has been remarkably improved by updating the numerical approximation methods. The improved accuracy of numerical approximation of intractable integrals leads to accurate characterization of original pdfs, resulting in an enhanced estimation accuracy. The literature in this category can be further classified into two sub-categories:cubature rule-based filters and quadrature rule-based filters.Cubature rule-based filtering begins with cubature Kalman filter (CKF) [28], which is further modified with several variants [29]–[31]. Other important developments in this subcategory are cubature quadrature Kalman filter (CQKF) and its variants [32]–[34], high-degree CKF (HDCKF) [35] and high-degree CQKF (HDCQKF) [36]. The objective of sequentially developed filters is to improve the estimation accuracy. However, the computational burden is also increased with every development. Under the quadrature rulebased filtering, the literature begins with Gauss-Hermite filter(GHF) [37], [38] and its variants [39]–[41]. The estimation accuracy of GHF is better than the cubature rule-based filters.However, it failed to attract the practitioners due to its high computational burden. A series of further developments,namely the sparse-grid GHF (SGHF) [42]–[44], multiple GHF(MGHF) [45], [46], and adaptive SGHF (ASGHF) [47],appeared to reduce the computational burden. Another interesting development on improving the numerical approximation accuracy is transformed filtering [27], [34],[48], [49], where the sample points used for numerical approximation are orthogonally transformed. The transformed filtering could enhance the estimation accuracy without adding extra computational burden.

The second category reformulates the Gaussian filtering approach in different aspects. The square-root filtering [22],[33], [39], [50]–[52], and the Gaussian-sum filtering [30],[53]–[55] are popular developments in this category. The objective of square-root filtering is to preclude the positivedefinite requirement of error covariance matrix (essentially required in traditional Gaussian filters). It does not impact the estimation accuracy, but extends the filter applicability to the systems where the positive-definiteness is not guaranteed. The Gaussian-sum filtering, on the other hand, improves the estimation accuracy by approximating the unknown pdfs with multiple Gaussian components instead of a single Gaussian.

In the third category, our discussion is focused on removing the constraint of discrete-time formulation of process dynamics. Under this constraint, the process dynamics is approximated as discrete, though it generally comes from continuous physical laws. In many problems (especially, if the sampling interval is large), this approximation is significant enough to harm the estimation accuracy. A continuousdiscrete filtering technique [56]–[60] is developed to mitigate this approximation.

The literature witnesses other review papers pertaining to the Gaussian filtering, such as [61] and [62]. However, the scope of this review is widely different from them, more extensive, and more recent. Reference [61] was published in 2012, while many of the filtering techniques discussed in this review were introduced after that. Reference [61] discusses the computational aspects of the UKF only (out of all the filtering techniques reviewed in this paper), though a very brief discussion about the idea of CKF and GHF is also provided. It provides no discussion about square-root filtering,Gaussian-sum filtering, continuous-discrete filtering, and filtering with transformed sample points. The survey in [62] is focused more on the EKF and its extensions, though it puts some highlight on the UKF and the Gaussian-sum filtering.

The remaining part of this paper is organized as follows:Section II revisits the conventional Bayesian framework and the Gaussian filtering approach. A brief discussion about the UKF formulation is provided in Section III. Cubature rulebased filters are discussed in Section IV, followed by a brief discussion on quadrature rule-based filters in Section V.Section VI highlights the effect of orthogonal transformation over sample points. Sections VII and VIII describe squareroot filtering and Gaussian-sum filtering, respectively. Section IX introduces the continuous-discrete filtering method. In Section X, the Gaussian filters are implemented with real-life nonlinear filtering problems, and their performance is analyzed with simulation results. Finally, discussions and conclusions are drawn in Section XI. A moment-based derivation of estimates is provided in Appendix A, followed by a brief discussion on Gaussian sigma point Kalman filtering algorithm in Appendix B.

II. Bayesian Framework of Filtering

The dynamic state space model of a system is represented with state and measurement equations, as [1]

where xk∈ Rnand yk∈ Rdare state and measurement variables at the kth instant; k ∈{0,1,...} , ϕk:xk−1→xkand true and estimated trajectories concludes a successful tracking using the CD-UKF and CD-CKF. The mean of absolute relative error for the CD-UKF and CD-CKF obtained over 200 Monte-Carlo executions are shown in Table II. The relative error is not analyzed along the height (state 5 and 6) as a constant height motion is considered. Moreover, the RMSEs obtained from the CD-UKF and CD-CKF are compared with their discrete-time counterparts, UKF and CKF, in Fig.7. The figure concludes an arbitrarily large RMSE, such that divergence for the discretetime filters, the UKF, and CKF.

The covariance matrices failed to satisfy the positivedefiniteness criteria during the implementation of the continuous-discrete filters. Subsequently, the traditional filtering approaches failed. However, a square-root extension could help in successful implementation, which validates the importance of square-root filtering.

Fig.6. Problem 2: True and estimated plots of x-y position for continuousdiscrete filters.

TABLE II Mean of Absolute Relative Error for Continuous-Discrete Filters

Fig.7. Problem 2: RMSE plots for CD-UKF, CD-CKF, and their discretetime counterparts, UKF, and CKF.

XI. Discussions and Conclusions

The Bayesian framework of filtering has been a common choice among practitioners for several decades. It is a conceptual solution, and a commonly practiced analytical interpretation is Gaussian filtering, which offers high estimation accuracy at low computational cost. The early Gaussian filters, the EKF and its variants, suffered from several limitations due to derivative-based implementation. A derivative-free approach, named as UKF, was introduced in the nineties based on numerical approximation of intractable integrals. The UKF shows several advantages over the derivative-based filtering. Subsequently, the research continued further, leading to many derivative-free filters developed by advancing the numerical approximation techniques. This review classifies these developments in two categories: cubature rule-based filters and quadrature rulebased filters. The cubature rule-based filters decompose the intractable integrals into spherical and radial sub-parts. The spherical sub-part is approximated using the spherical-cubature rule, while the radial sub-part is approximated using the Gauss-Laguerre quadrature rule. Several developments appeared in this category by offering different order of approximation for the spherical and radial sub-parts. Some popular developments are CKF, CQKF, HDCKF, and HDCQKF. The quadrature rulebased filters, on the other side, implement a univariate Gauss-Hermite quadrature rule for the numerical approximation. An additional mathematical law is implemented for extending the univariate rule in multivariate domain. The filters in this category are known for high estimation accuracy, but often inapplicable due to high computational cost. The initial development was GHF, which is followed by several developments, like SGHF, ASGHF, and MGHF, to improve the computational efficiency.

The quadrature rule-based filters are preferred over the cubataure rule-based filters if the estimation accuracy is crucial and a large computational budget is allotted. On the other hand, the practitioners may choose to cut the computational budget by using cubature rule-based filters if the estimation accuracy is not very crucial. Both the cubature rule-based filtering and quadrature rule-based filtering offer different choices (with varying estimation accuracy and computational budget) to reach a trade-off between the desired estimation accuracy and the available computational budget.

The literature consists of some developments to modify the traditional Gaussian filtering approach and the Bayesian framework as well. Some popular modifications in the Gaussian filtering approach are square-root filtering and Gaussian-sum filtering. The square-root filtering aims to extend the filter applicability, while the Gaussian-sum filtering is motivated to improve the estimation accuracy. In the modification to the Bayesian framework, this paper reviews the continuous-discrete filtering methods.

Appendix A Estimates in Terms of Moments

The Gaussian filters implement a numerical approximation technique in the computation of estimates. The numerical approximation techniques are accurate only up to a particular order of Taylor series expansion. The higher-order terms contribute to the approximation error, which further contributes to estimation error. Subsequently, the representation of estimates in terms of moments helps in

[2]R. G. Brown and P. Y. C. Hwang, Introduction to Random Signals and Applied Kalman Filtering. New York, USA: Wiley, 1997.

[3]B . D. O. Anderson and J. B. Moore, Optimal Filtering. Englewood Cliffs, USA: Prentice Hall, 1979.

[4]A . Gelb, Applied Optimal Estimation. Boston, USA: MIT Press, 1974.

[5]D . Simon, Optimal State Estimation. New Jersey, USA: Wiley, 2006.

[6]M . Abo, O. W. Marquez, J. McNames, R. Hornero, T. Trong, and B.Goldstein, “Adaptive modeling and spectral estimation of nonstationary biomedical signals based on Kalman filtering,” IEEE Trans. Biomed.Eng., vol. 52, no. 8, pp. 1485–1489, Aug. 2005.

[7]C . Wells, “The Kalman filter in finance,” Springer, vol. 32, 2013.

[8]P . L. Houtekamer and H. L. Mitchell, “Data assimilation using an ensemble kalman filter technique,” Mon. Wea. Rev., vol. 126, no. 3,pp. 796–811, Mar. 1998.

[9]S . Särkkä, Bayesian Filtering and Smoothing. Cambridge, USA:Cambridge University Press, 2013.

[10]A . H. Jazwinski, Stochastic Processes and Filtering Theory. New York,USA: Dover Publications, 2007.

[11]R . E. Kalman, “A new approach to linear filtering and prediction problems,” J. Basic Eng., vol. 82, no. 1, pp. 35–45, Mar. 1960.

[12]D . Godard, “Channel equalization using a Kalman filter for fast data transmission,” IBM J. Res. Dev., vol. 18, no. 3, pp. 267–273, May 1974.

[13]R . A. Singer, “Estimating optimal tracking filter performance for manned maneuvering targets,” IEEE Trans. Aerosp. Electron. Syst.,vol. AES-6, no. 4, pp. 473–483, Jul. 1970.

[14]M . Athans, R. P. Wishner, and A. Bertolini, “Suboptimal state estimation for continuous-time nonlinear systems from discrete noisy measurements,” IEEE Trans. Autom. Control, vol. 13, no. 5,pp. 504–514, Oct. 1968.

[15]S . K. Rao, “Modified gain extended Kalman filter with application to bearings-only passive manoeuvring target tracking,” IET Proc. Radar Sonar Navig., vol. 152, no. 4, pp. 239–244, Aug. 2005.

[16]T . Song and J. Speyer, “A stochastic analysis of a modified gain extended Kalman filter with applications to estimation with bearings only measurements,” IEEE Trans. Autom. Control, vol. 30, no. 10,pp. 940–949, Oct. 1985.

[17]S . J. Julier and J. K. Uhlmann, “New extension of the Kalman filter to nonlinear systems,” in Proc. SPIE 3068, Signal Processing, Sensor Fusion, and Target Recognition VI, 1997.

[18]S . Julier, J. Uhlmann, and H. F. Durrant-Whyte, “A new method for the nonlinear transformation of means and covariances in filters and estimators,” IEEE Trans. Autom. Control, vol. 45, no. 3, pp. 477–482,Mar. 2000.

[19]S . J. Julier and J. K. Uhlmann, “Unscented filtering and nonlinear estimation,” Proc. IEEE, vol. 92, no. 3, pp. 401–422, Mar. 2004.

[20]S . J. Julier and J. K. Uhlmann, “Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations,” in Proc.American Control Conf., Anchorage, USA,2002, pp. 887–892.

[21]S . J. Julier, “The scaled unscented transformation,” in Proc. American Control Conf., Anchorage, USA, 2002, pp. 4555–4559.

[22]R . van der Merwe and E. A. Wan, “The square-root unscented kalman filter for state and parameter-estimation,” in Proc. IEEE Int. Conf.Acoustics, Speech, and Signal Processing, Salt Lake City, USA, 2001,pp. 3461–3464.

[23]R . van der Merwe and E. A. Wan, “Efficient derivative-free Kalman filters for online learning,” in Proc. European Symp. Artificial Neural Networks, Bruges, Belgium, 2001, pp. 205–210.

[24]Y . X. Wu, D. W. Hu, M. P. Wu, and X. P. Hu, “Unscented Kalman filtering for additive noise case: Augmented versus nonaugmented,”IEEE Signal Process. Lett., vol. 12, no. 5, pp. 357–360, May 2005.

[25]Y . Lei, D. Xia, K. Erazo, and S. Nagarajaiah, “A novel unscented Kalman filter for recursive state-input-system identification of nonlinear systems,” Mech. Sys. Sign. Proc., vol. 127, pp. 120–135, Jul. 2019.

[26]Z . Jiang, Q. Song, Y. Q. He, and J. D. Han, “A novel adaptive unscented Kalman filter for nonlinear estimation,” in Proc. 46th IEEE Conf. Decision and Control, New Orleans, USA, 2007, pp. 4293–4298.

[27]L . B. Chang, B. Q. Hu, A. Li, and F. J. Qin, “Transformed unscented Kalman filter,” IEEE Trans. Autom. Control, vol. 58, no. 1, pp. 252–257,Jan. 2013.

[28]I . Arasaratnam and S. Haykin, “Cubature Kalman filters,” IEEE Trans.Autom. Control, vol. 54, no. 6, pp. 1254–1269, Jun. 2009.

[29]J . Mu and Y. L. Cai, “Iterated cubature Kalman filter and its application,” in Proc. IEEE Int. Conf. Cyber Tech. in Automation,Control, and Intelligent Systems, Kunming, China, 2011, pp. 33–37.

[30]P . H. Leong, S. Arulampalam, T. H. Lamahewa, and T. D. Abhayapala,“A Gaussian-sum based cubature Kalman filter for bearings-only tracking,” IEEE Trans. Aerosp. Electron. Syst., vol. 49, no. 2,pp. 1161–1176, Apr. 2013.

[31]S . Y. Wang, J. C. Feng, and C. K. Tse, “Spherical simplex-radial cubature Kalman filter,” IEEE Signal Process. Lett., vol. 21, no. 1,pp. 43–46, Jan. 2014.

[32]S . Bhaumik and Swati, “Cubature quadrature Kalman filter,” IET Signal Process., vol. 7, no. 7, pp. 533–541, Sept. 2013.

[33]S . Bhaumik and Swati, “Square-root cubature-quadrature Kalman filter,” Asian J. Control, vol. 16, no. 2, pp. 617–622, Mar. 2014.

[34]A . K. Singh and S. Bhaumik, “Transformed cubature quadrature Kalman filter,” IET Sign. Process., vol. 11, no. 9, pp. 1095–1103, Jul.2017.

[35]B . Jia, M. Xin, and Y. Cheng, “High-degree cubature Kalman filter,”Automatica, vol. 49, no. 2, pp. 510–518, Feb. 2013.

[36]A . K. Singh and S. Bhaumik, “Higher degree cubature quadrature Kalman filter,” Int. J. Control Autom. Syst., vol. 13, no. 5,pp. 1097–1105, Oct. 2015.

[37]K . Ito and K. Xiong, “Gaussian filters for nonlinear filtering problems,”IEEE Trans. Autom. Control, vol. 45, no. 5, pp. 910–927, May 2000.

[38]I . Arasaratnam, S. Haykin, and R. J. Elliott, “Discrete-time nonlinear filtering algorithms using Gauss-Hermite quadrature,” Proc. IEEE,vol. 95, no. 5, pp. 953–977, May 2007.

[39]I . Arasaratnam and S. Haykin, “Square-root quadrature Kalman filtering,” IEEE Trans. Signal Process., vol. 56, no. 6, pp. 2589–2593,Jun. 2008.

[40]H . Singer, “Generalized gauss-hermite filtering,” AStA Adv. Stat. Anal.,vol. 92, no. 2, pp. 179–195, May 2008.

[41]H . Singer, “Conditional Gauss-Hermite filtering with application to volatility estimation,” IEEE Trans. Autom. Contr., vol. 60, no. 9,pp. 2476–2481, Sept. 2015.

[42]B . Jia, M. Xin, and Y. Cheng, “Sparse-grid quadrature nonlinear filtering,” Automatica, vol. 48, no. 2, pp. 327–341, Feb. 2012.

[43]B . Jia, M. Xin, and Y. Cheng, “Sparse Gauss-Hermite quadrature filter with application to spacecraft attitude estimation,” J. Guid. Control Dyn., vol. 34, no. 2, pp. 367–379, Mar-Apr. 2011.

[44]B . Jia, M. Xin, and Y. Cheng, “Comparison of the sparse-grid quadrature rule and the cubature rule in nonlinear filtering,” in Proc.IEEE 51st IEEE Conf. Decision and Control, Maui, USA, 2012, pp.6022–6027.

[45]P . Closas, C. Fernandez-Prades, and J. Vila-Valls, “Multiple quadrature Kalman filtering,” IEEE Trans. Signal Process., vol. 60, no. 12,pp. 6125–6137, Dec. 2012.

[46]R . Radhakrishnan, A. K. Singh, S. Bhaumik, and N. K. Tomar,“Multiple sparse-grid Gauss-Hermite filtering,” Appl. Math. Model.,vol. 40, no. 7-8, pp. 4441–4450, Apr. 2016.

[47]A . K. Singh, R. Radhakrishnan, S. Bhaumik, and P. Date, “Adaptive sparse-grid Gauss–Hermite filter,” J. Comput. Appl. Math., vol. 342,pp. 305–316, Nov. 2018.

[48]A . K. Singh and S. Bhaumik, “Nonlinear estimation using transformed Gauss-Hermite quadrature points,” in Proc. IEEE Int. Conf. Signal Processing, Computing and Control, Solan, India, 2013, pp. 1–4.

[49]A . K. Singh, S. Bhaumik, and R. Radhakrishnan, “Nonlinear estimation with transformed cubature quadrature points, ” in Proc. IEEE Int. Symp.Signal Processing and Information Technology, Noida, India, 2014, pp.428–432.

[50]D . Potnuru, K. P. B. Chandra, I. Arasaratnam, D. W. Gu, K. A. Mary,and S. B. Ch, “Derivative-free square-root cubature Kalman filter for non-linear brushless DC motors,” IET Electric Power Appl., vol. 10,no. 5, pp. 419–429, Apr. 2016.

[51]K . P. B. Chandra, D. W. Gu, and I. Postlethwaite, “Square root cubature information filter,” IEEE Sens. J., vol. 13, no. 2, pp. 750–758, Feb. 2013.

[52]X. J. Tang, Z. B. Liu, and J. S. Zhang, “Square-root quaternion cubature Kalman filtering for spacecraft attitude estimation,” Acta Astronaut.,vol. 76, pp. 84–94, Jul-Aug. 2012.

[53]D . Alspach and H. Sorenson, “Nonlinear Bayesian estimation using Gaussian sum approximations,” IEEE Trans. Autom. Control, vol. 17,no. 4, pp. 439–448, Aug. 1972.

[54]P . H. Leong, S. Arulampalam, T. A. Lamahewa, and T. D. Abhayapala,“Gaussian-sum cubature Kalman filter with improved robustness for bearings-only tracking,” IEEE Signal Process. Lett., vol. 21, no. 5,pp. 513–517, May 2014.

[55]G . Terejanu, P. Singla, T. Singh, and P. D. Scott, “Adaptive Gaussian sum filter for nonlinear Bayesian estimation,” IEEE Trans. Autom.Control, vol. 56, no. 9, pp. 2151–2156, Sept. 2011.

[56]A . H. Jazwinski, Stochastic Processes and Filtering Theory. New York,USA: Academic, 1970.

[57]J . B. Jorgensen, P. G. Thomsen, H. Madsen, and M. R. Kristensen, “A computationally efficient and robust implementation of the continuousdiscrete extended Kalman filter,” in Proc. American Control Conf.,New York, USA, 2007, pp. 3706–3712.

[58]S . Sarkka, “On unscented Kalman filtering for state estimation of continuous-time nonlinear systems,” IEEE Trans. Autom. Control,vol. 52, no. 9, pp. 1631–1641, Sept. 2007.

[59]I . Arasaratnam, S. Haykin, and T. R. Hurd, “Cubature Kalman filtering for continuous-discrete systems: theory and simulations,” IEEE Trans.Signal Process., vol. 58, no. 10, pp. 4977–4993, Oct. 2010.

[60]G . Y. Kulikov and M. V. Kulikova, “Accurate numerical implementation of the continuous-discrete extended Kalman filter,”IEEE Trans. Auto. Cont., vol. 59, no. 1, pp. 273–279, Jan. 2014.

[61]S . C. Patwardhan, S. Narasimhan, P. Jagadeesan, B. Gopaluni, and S. L.Shah, “Nonlinear Bayesian state estimation: A review of recent developments,” Control Eng. Pract., vol. 20, no. 10, pp. 933–953, Oct.2012.

[62]H . Z. Fang, N. Tian, Y. B. Wang, M. C. Zhou, and M. A. Haile,“Nonlinear Bayesian estimation: From Kalman filtering to a broader horizon,” IEEE/CAA J. Autom. Sinica, vol. 5, no. 2, pp. 401–417, Mar.2018.

[63]H . Kushner, “Approximations to optimal nonlinear filters,” IEEE Trans.Autom. Control, vol. 12, no. 5, pp. 546–556, Oct. 1967.

[64]D . Reid, “An algorithm for tracking multiple targets,” IEEE Trans.Autom. Control, vol. 24, no. 6, pp. 843–854, Dec. 1979.

[65]R . van der Merwe and E. Wan, “Sigma-point Kalman filters for probabilistic inference in dynamic state-space models,” in Proc.Workshop on Advances in Machine Learning. 2004.

[66]C . S. Manohar and D. Roy, “Monte Carlo filters for identification of nonlinear structural dynamical systems,” Sadhana, vol. 31, no. 4,pp. 399–427, Aug. 2006.

[67]V . K. Mishra, R. Radhakrishnan, A. K. Singh, and S. Bhaumik,“Bayesian filters for parameter identification of duffing oscillator,”IFAC-PapersOnLine, vol. 51, no. 1, pp. 425–430, Jan. 2018.

[68]R . H. Zhan and J. W. Wan, “Iterated unscented Kalman filter for passive target tracking,” IEEE Trans. Aerosp. Electron. Syst., vol. 43,no. 3, pp. 1155–1163, Jul. 2007.

[69]S . Jafarzadeh, C. Lascu, and M. S. Fadali, “State estimation of induction motor drives using the unscented Kalman filter,” IEEE Trans. Ind.Electron., vol. 59, no. 11, pp. 4207–4216, Nov. 2012.

[70]P . H. Li, T. W. Zhang, and B. Ma, “Unscented Kalman filter for visual curve tracking,” Image Vision Comput., vol. 22, no. 2, pp. 157–164, Feb.2004.

[71]M . Sepasi and F. Sassani, “On-line fault diagnosis of hydraulic systems using unscented Kalman filter,” Int. J. Control Autom. Syst., vol. 8,no. 1, pp. 149–156, Feb. 2010.

[72]A . Genz, “Fully symmetric interpolatory rules for multiple integrals over hyper-spherical surfaces,” J. Comput. Appl. Math., vol. 157, no. 1,pp. 187–195, Aug. 2003.

[73]A . H. Stroud, Approximate Calculation of Multiple Integrals.Englewood Cliffs, USA: Prentice-Hall, 1971.

[74]V . I. Krylov, Approximate Calculation of Integrals. New York, USA:Dover, 2006.

[75]F . B. Hildebrand, Introduction to Numerical Analysis. 2nd ed. New York, USA: McGraw Hill, 1973.

[76]J . Zarei, E. Shokri, and H. R. Karimi, “Convergence analysis of cubature Kalman filter,” in Proc. European Control Conf., Strasbourg,France, 2014.

[77]M . Havlicek, K. J. Friston, J. Jan, M. Brazdil, and V. D. Calhoun,“Dynamic modeling of neuronal responses in fMRI using cubature Kalman filtering,” NeuroImage, vol. 56, no. 4, pp. 2109–2128, Jun.2011.

[78]W . L. Li and Y. M. Jia, “Location of mobile station with maneuvers using an IMM-based cubature Kalman filter,” IEEE Trans. Ind.Electron., vol. 59, no. 11, pp. 4338–4348, Nov. 2012.

[79]Y . Wu, D. Hu, M. Wu, and X. Hu, “A numerical-integration perspective on Gaussian filters,” IEEE Trans. Signal Process., vol. 54, no. 8,pp. 2910–2921, Aug. 2006.

[80]R . Cools and P. Rabinowitz, “Monomial cubature rules since “Stroud”:A compilation,” J. Comput. Appl. Math., vol. 48, no. 3, pp. 309–326,Nov. 1993.

[81]F . B. Hildebrand, Introduction to Numerical Analysis. 2nd ed. St.Mineola, USA: Dover, 1987.

[82]S . S. Bonan and D. S. Clark, “Estimates of the Hermite and the Freud polynomials,” J. Approx. Theory, vol. 63, no. 2, pp. 210–224, Nov. 1990.

[83]Y . H. Ku and M. Drubin, “Network synthesis using legendre and Hermite polynomials,” J. Frank. Inst., vol. 273, no. 2, pp. 138–157, Feb.1962.

[84]A . K. Singh, K. Kumar, Swati, and S. Bhaumik “Cubature and quadrature based continuous-discrete filters for maneuvering target tracking,” in Proc. 21st Int. Conf. Information Fusion, Cambridge,2018.

[85]S . A. Smolyak, “Quadrature and interpolation formulas for tensor products of certain classes of functions,” Dokl. Akad. Nauk SSSR,vol. 148, no. 5, pp. 1042–1045, 1963.

[86]T . Gerstner and M. Griebel, “Dimension-adaptive tensor-product quadrature,” Computing, vol. 71, no. 1, pp. 65–87, Aug. 2003.

[87]M . S. Grewal, L. R. Weill, and A. P. Andrews, Global Positioning Systems, Inertial Navigation, and Integration. Hoboken, USA: Wiley,2001.

[88]K . J. Astrom, Introduction to Stochastic Control Theory. New York,USA: Dover, 1970.

[89]G . Terejanu, P. Singla, T. Singh, and P. D. Scott, “Uncertainty propagation for nonlinear dynamic systems using Gaussian mixture models,” J. Guid. Control Dyn., vol. 31, no. 6, pp. 1623–1633, Nov.-Dec. 2008.

[90]M . Kumar, S. Chakravorty, P. Singla, and J. L. Junkins, “The partition of unity finite element approach with hp-refinement for the stationary Fokker-Planck equation,” J. Sound Vibr., vol. 327, no. 1-2, Oct. 2009.

[91]P . E. Kloeden and E. Platen, Numerical Solution of Stochastic Differential Equations. Berlin, Germany: Springer, 1991.