基于改进果蝇算法优化PNN的变压器故障诊断研究

郭晓芸, 李海明, 许赟杰

(上海电力大学 计算机科学与技术学院, 上海 200090)

电力变压器是配电系统中的重要设备。由于其内部结构复杂,电场及热场分布不均等诸多因素,事故率仍然很高,因此研究精确有效的变压器故障诊断对电力部门而言显得格外重要[1]。

电力变压器产生故障的原因复杂且不易直观看出,故判断故障性质和产生位置难度增大[2]。油中溶解气体分析(Dissolved Gas Analysis,DGA)是变压器故障诊断中最常用的方法,是通过分析变压器油中溶解气体的相对含量来判断故障类型的[3]。神经网络在识别变压器故障时容易陷入局部最优,收敛速度慢。概率神经网络(Probablistic Neural Network,PNN)具有训练时间短,结构固定,能产生贝叶斯后验概率输出等优点,适合解决模式分类问题[4]。果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)具有简单易理解、易调节、参数少、快速收敛到全局最优等优点[5-6]。

本文提出了一种定向变步长的果蝇算法(Directional Variable Step Fruit Fly Optimization Algorithm,DVSFOA),解决了果蝇算法中存在的搜索步长变化的问题,提高了其整体的寻优能力,并将DVSFOA与PNN相结合,优化了PNN中的平滑因子,降低了人为因素对神经网络的影响,具有较强的结构自适应能力和容错能力。将该模型应用到变压器故障诊断中,能有效地对变压器故障进行诊断,且准确率较高。

1 PNN模型

PNN是一种前向型神经网络,利用高斯函数作为基函数与Parzen窗法估计得到概率密度,然后与贝叶斯最小风险准则相结合发展而来的[7]。

利用PNN模型强大的非线性分类能力,构造了一个具有监督功能的分类器模型,将其应用到模式分类中,具有较高的精确率和容错率[8]。PNN通常由4层组成,分别是输入层、模式层、求和层和输出层[9]。其拓扑结构如图1所示。

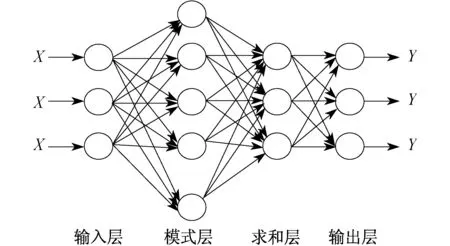
图1 PNN拓扑结构

输入层作为PNN模型的入口,主要将特征向量传入网络,节点的个数等于样本的特征维度。模式层紧接着输入层,其通过权值与上一层连接,主要用于识别传入的特征向量与训练集中各类别的匹配关系。求和层求出相同类别测试样本所对应的模式层节点输出之和,节点个数等于训练样本的类别个数。输出层对求和层的输出进行归一化处理,求出测试样本不同类别的概率,根据概率的大小判断测试样本的类别。

输入层和模式层之间通过一个高斯函数连接,其函数公式为

(1)

式中:lg——g类的数量;

n——特征向量的个数;

σ——平滑因子;

xi——输入层输入的特征向量。

PNN作为一个多分类器,具有结构简单、学习速度快、分类能力强、容错性好、噪声容忍度高等优点。PNN模型中,唯一需要调整的参数是平滑因子σ。如果σ值太小,则PNN是对单独训练的样本进行隔离,其本质上成为了最近邻域分类器;如果σ太大,则PNN不能完全分辨细节,尤其对于界限不是特别明显的不同类别,更无法达到理想的分类效果,这时的PNN近似于线性分类器。因此,确定合适的σ值是PNN的关键问题。

2 基于DVSFOA的PNN参数优化

2.1 果蝇优化算法

FOA是受果蝇觅食行为启发而提出的一种仿生智能优化算法,是一种全局优化方法[10]。果蝇因自身嗅觉和视觉而具有对外部环境极为敏感的特性[11]。在搜寻食物时,每一只个体通过优异的嗅觉获取周边大范围中的各种气味,并从中辨别出食物来源的大致位置,同时向群体中的其他果蝇个体分享自身获得的气味信息,之后群体中的果蝇会比较相互之间分享的信息,辨别出最佳气味的来源,同时通过各自的视觉器官向该位置聚集而去。果蝇迭代搜索食物过程如图2所示。

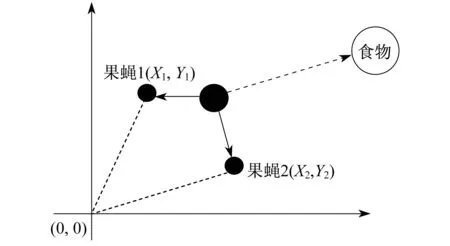
图2 果蝇迭代搜索食物过程

根据果蝇觅食行为特性,将FOA归纳为以下步骤[12]。

(1) 设定果蝇种群规模Pop_size和最大迭代次数Max_iter,初始化群体位置(X_axis,Y_axis);

(2) 将[-1,1]内的随机值作为每一次迭代中果蝇的搜索步长,其值的正负分别表示果蝇在X轴和Y轴上的移动方向,值的大小表示移动的距离[13],即

(2)

(3) 计算果蝇距离原点的距离Dist和味道浓度判定值Si

(3)

(4)

(4) 将Si作为参数传入适应度函数function中[14],计算得出味道浓度Smell_den

Smell_den=function(Si)

(5)

(5) 求出果蝇味道浓度的极大值并记录

Smell_Best=max(Smell)

Best_Index=arg_max(Smell)

(6)

(6) 记录味道浓度最大的位置

(7)

(7) 迭代寻优,重复搜索执行步骤。

2.2 改进果蝇优化PNN

文献[15]将FOA与目前常用的群体智能优化算法进行寻优能力对比,发现相较于其他智能优化算法,FOA具有很强的全局寻优能力,较低的算法复杂度,但是其局部寻优能力不足,容易过早熟。实际上,FOA寻优能力的变化取决于每一次迭代时果蝇群体搜索步长的变化。由于搜索步长的取值在每一次的迭代中都是随机的,因此原本的FOA无法控制每一次果蝇的移动方向和距离。针对该问题,本文提出了定向变步长的思路,对FOA中的搜索步长进行了改进。

改进的算法公式为

(8)

式中:Lm——味道浓度达到最大值时果蝇所移动的方向;

L[Best_Index]——味道浓度达到最大值时果蝇所移动的步长;

Xi——果蝇迭代位置横坐标;

Yi——果蝇迭代位置纵坐标。

在上一次迭代结束时记录下的味道浓度达到最大值时果蝇所移动的步长和方向,并按此方向继续搜寻,通过rand()函数可以返回一个或一组服从标准正态分布的随机样本值。由于已经确定了果蝇的前进方向,因此考虑扩大每只果蝇搜索步长的取值。本文认为,取(0,5)之间的随机实数能够囊括更大的范围。比起非定向的FOA来说,该取值确定了每一次前进的方向,向着浓度更高的方向寻找,并且适当地扩大了前进的步长,可以更快速地寻找到最优解,而且具备逃离局部最优解的能力。

2.3 DVSFOAPNN故障诊断模型

PNN是一种前向型神经网络,输入层和模式层之间的连接是通过将高斯函数作为基函数实现非线性分类,将FOA的Si作为参数传入PNN的高斯函数中,从而实现FOA与PNN的结合,提高诊断性能。DVSFOA-PNN故障诊断流程如图3所示。

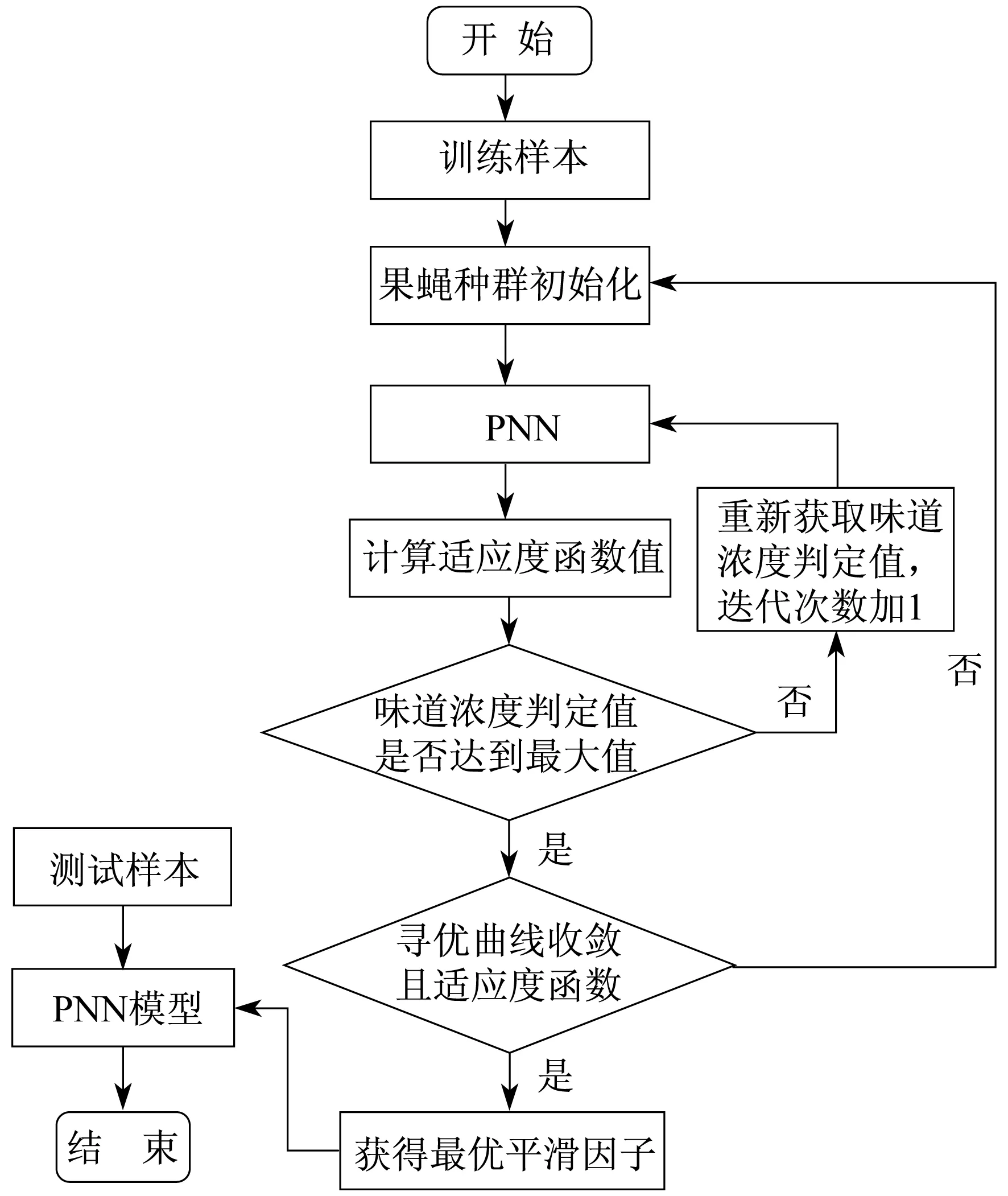
图3 DVSFOAPNN故障诊断流程

2.4 DVSFOA与FOA对比分析

FOA实现步骤过程如下。

步骤1 初始化果蝇群体规模和迭代次数;

步骤2 为果蝇群体的初始位置X_axis和Y_axis赋予随机值;

步骤3X[i]=X_axis+ (2×rand(0,1)-1);

步骤4Y[i]=Y_axis+ (2×rand(0,1)-1);

步骤5Dist=np.sqrt(X[i]**2+Y[i]**2);

步骤6S[i]=1/Dist;

步骤7 Smell[i]=function(S[i]) # 将距离传入适应度函数计算;

步骤8 bestsmell 0t,bestindex=np.max(Smell), np.argmax(Smell);#获取味道浓度最大的值和其所在位置的下标;

步骤9 判断味道浓度,迭代寻优。

DVSFOA实现步骤如下。

步骤1 初始化果蝇群体规模和迭代次数;

步骤2 为果蝇群体的初始位置X_axis和Y_axis赋予随机值;

步骤3 先运行一次FOA,通过LX和LY分别记录每一只果蝇的移动步长;

步骤4 BestLX=LX[bestindex] # 记录第一次FOA运行后,味道浓度达到最大值时X所移动的步长;

步骤5 BestLY=LY[bestindex] # 记录第一次FOA运行后,味道浓度达到最大值时Y所移动的步长;

步骤6X[i]=X_axis+BestLX/abs(BestLX) * Rand(0,5);

步骤7Y[i]=Y_axis+BestLY/abs(BestLY) * Rand(0,5);

步骤8LX=X[i]-X_axis # 记录本次果蝇在X轴上的移动步长;

步骤9LY=Y[i]-Y_axis # 记录本次果蝇在Y轴上的移动步长;

步骤10 Dist=np.sqrt(X[i]**2 +Y[i]**2);

步骤11S[i]=1/Dist;

步骤12 Smell[i]=function(S[i]) # 将距离传入适应度函数计算;

步骤13 bestsmell,IndexBest =np.max(Smell), np.argmax(Smell) # 获取味道浓度最大的值和其所在位置的下标。

由FOA中的步骤5和步骤6,可以看出每一只果蝇的移动方向和距离均是随机的,具有一定的不确定性。然而,在每一次的迭代Ij中,可以通过本次味道浓度最大值Best_smell的下标Best_index,对应地找到最佳味道浓度的位置(X[best_ndex],Y[Best_Index])。对于果蝇群体的初始位置X_axis和Y_axis而言,最佳味道浓度位置在X轴和Y轴上的变化方向可以为下一次迭代中的果蝇群体指明方向。

3 变压器DGA故障实验及结果分析

3.1 选取样本数据

本文对变电站油浸式电力变压器的故障气体数据进行分析,以验证本文所提算法模型对样本数据处理分类的效果。本文一共收集550组已经确定故障类型的DGA数据,以3∶1比例划分为训练样本与测试样本。其中411组训练数据用于参数寻优,139组样本数据用于验证优化后模型的诊断准确性。变压器故障样本数据分布如表3所示。

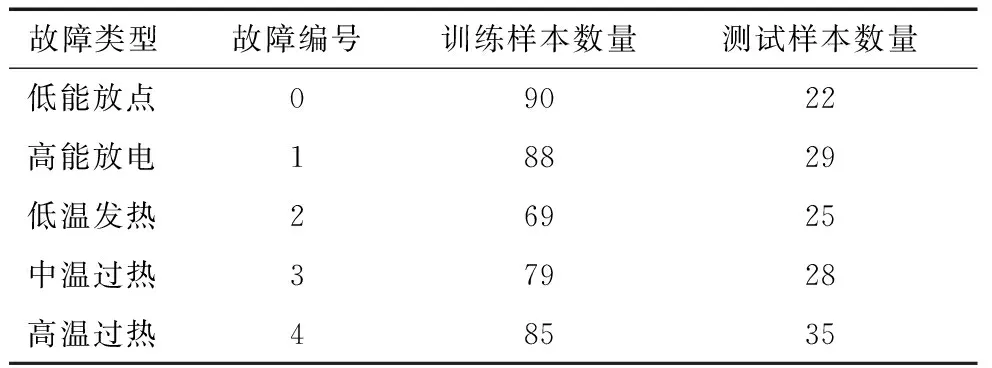
表3 变压器故障样本数据分布

3.2 三比值法

当变压器内部出现异常时,绝缘油中会产生气体,变压器油中溶解气体的组分和含量作为变压器异常的特征值予以记录。对这些气体进行分析,可以预测和诊断故障。求出具有相近溶解度和扩散系数的两种气体数据的比值,将CH4/H2,C2H2/C2H4,C2H4/C2H6的含量作为特征值P1,P2,P3输入DVSFOA-PNN网络中。输出5种对应的故障类型:低能放电T0,高能放电T1,低温发热T2,中温过热T3,高温过热T4。故障数据样本如表4所示。

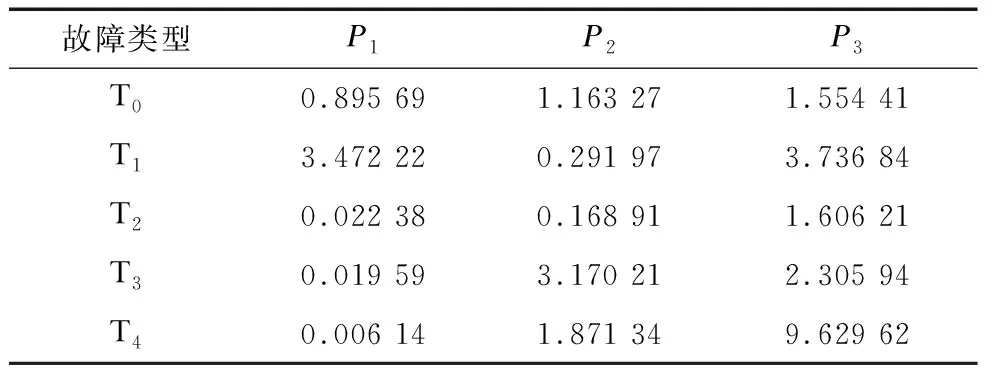
表4 故障数据样本

3.3 诊断结果与分析

设定果蝇群体规模为30,迭代次数为100,为了对比改进的测试结果,在参数相同的情况下,分别用FOA-PNN和DVSFOA-PNN建立变压器故障诊断模型得到优化结果,参数寻优精度曲线和均方根误差分析分别如图4和图5所示。

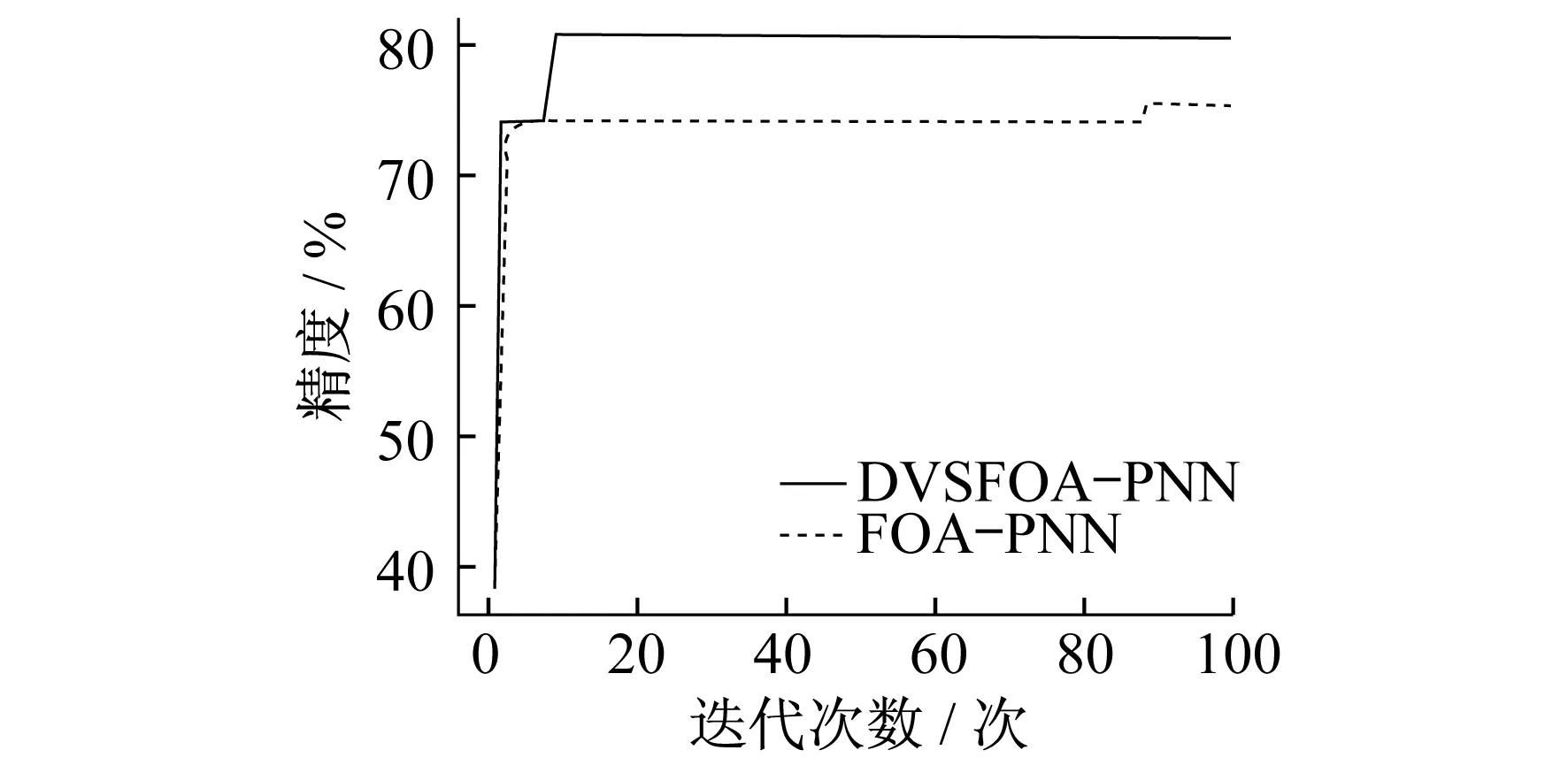
图4 参数寻优精度曲线

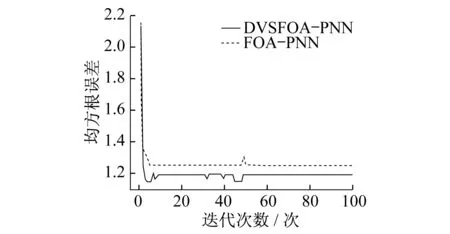
图5 均方根误差分析

在实验中,将平滑因子的初始值定为0.1,PNN的精度约为69.21%。通过图4可以看出,FOA和PNN结合后初始的精度为39.57%,但通过4次迭代后精度上升至72.68%,进入局部最优解,而后迭代至第88次跳出局部最优,最终平滑因子σ的取值为0.099 653。

DVSFOA-PNN的初始精度比FOA-PNN略低,为38.13%,但其通过2次迭代在第3次迭代中就达到了局部最优解,而后迭代至第9次就达到了82.41%的全局最优解,平滑因子σ最优解为0.023 558。由此可知,相比于FOA-PNN,DVSFOA-PNN的诊断精度更高。

另外,通过多次实验发现,FOA由于其每一次的移动方向和距离均为随机的原因,并不是每一次都可以跳出局部最优解,而DVSFOA在每一次的实验中均能达到更高的精度,且在达到更高精度的速度上具备更大的优势。

均方根误差用来衡量测试值与真值之间的偏差,描述离散程度,不是绝对误差。通过图5可知,训练过程中,FOA-PNN的均方根误差在第2次迭代后骤降至1.35,第4次迭代后缓慢下降至1.31后趋于平稳;DVSFOA-PNN的均方根误差在第3次迭代后骤降至1.09,第9次迭代后就趋于1.19,比FOA-PNN低了16.7%。这表明在迭代过程中,DVSFOA-PNN的分类偏离程度低于FOA-PNN,敏感反映了测量误差,DVSFOA-PNN的精度更高。

通过模型对测试样本进行分类,得到的PNN测试结果如图6所示,FOA-PNN测试结果如图7所示,DVSFOA-PNN测试结果如图8所示。其中,横坐标为对应样本数,纵坐标为故障类型标签。

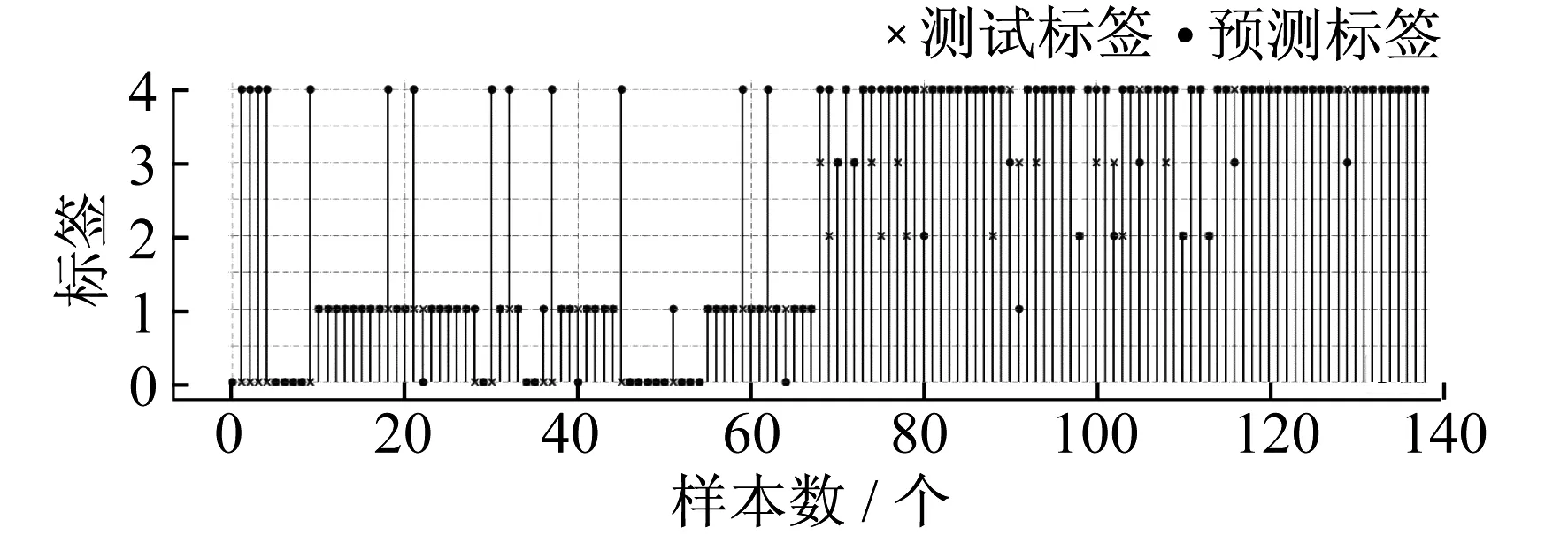
图6 PNN测试数据分类

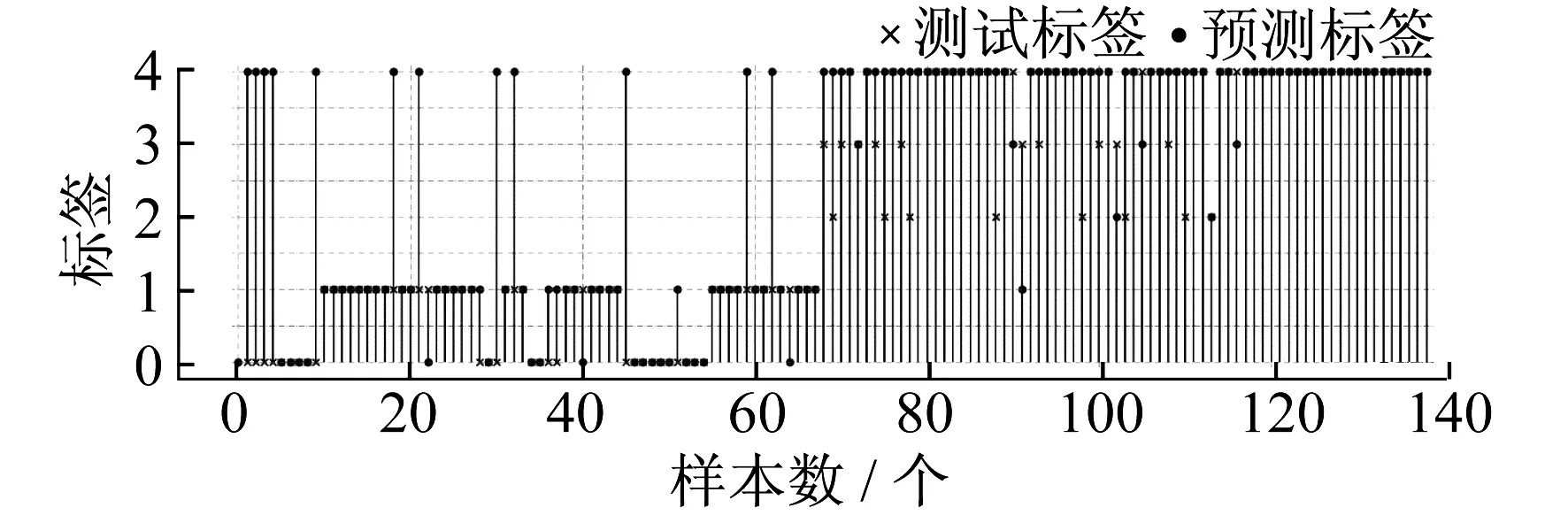
图7 FOAPNN测试数据分类

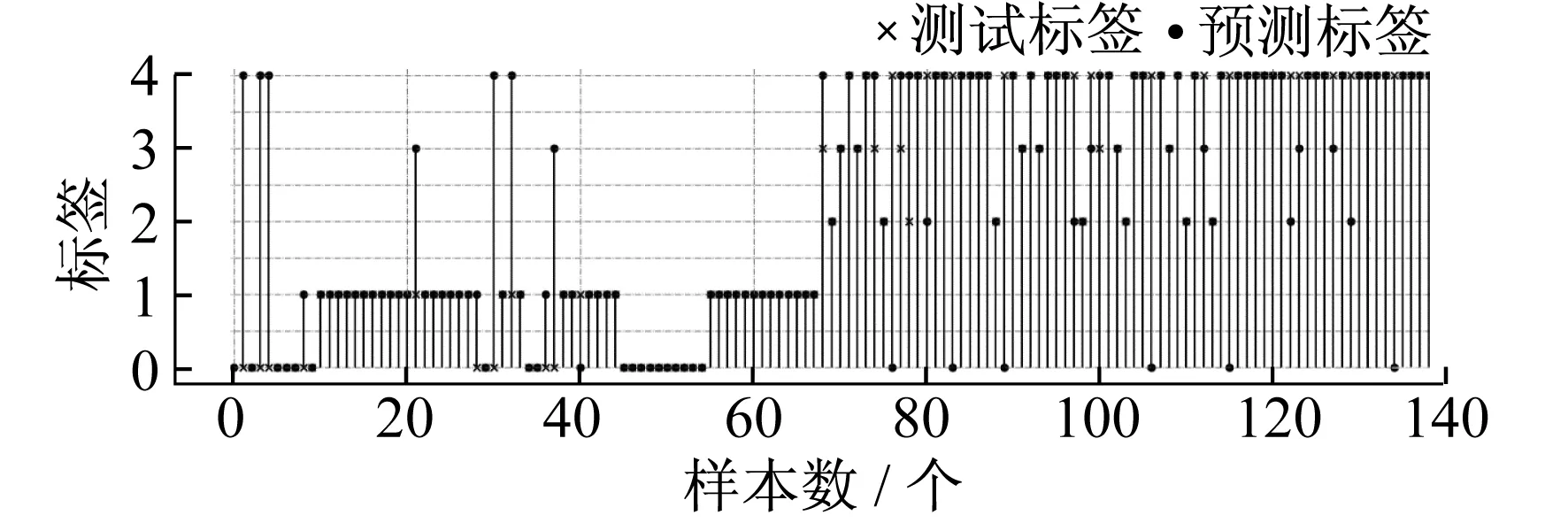
图8 DVSFOAPNN测试数据分类

表5为变压器故障诊断结果分析对比。

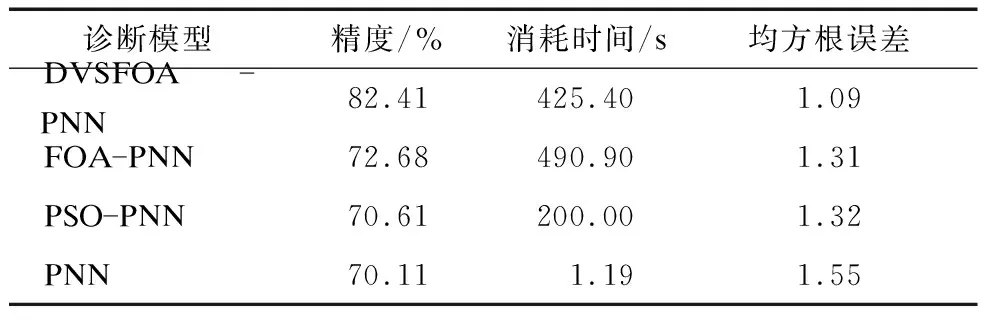
表5 变压器故障诊断结果分析

由表5可知,PNN精度为70.11%,PSO-PNN精度为70.61%,FOA-PNN精度为72.68%,DVSFOA-PNN精度为82.41%,表明改进过的算法分类精度高。对于复杂的多分类问题,用PNN和FOA-PNN均易陷入局部极值,精度降低,而DVSFOA-PNN的测试结果表现出较高的精度。耗时方面,由于本次试验设置的FOA和DVSFOA均具有30只果蝇和100次的迭代次数,总体需要3 000次的迭代,PNN无需迭代,耗时最短,而DVSFOA-PNN的消耗时间比FOA-PNN少15.4%。

4 结 论

本文在FOA的基础上,为每一次的迭代指定方向,即每一次的迭代方向均指向最优解的方向,最终得出DVSFOA。随后结合PNN模型,搭建了变压器故障诊断模型,通过实验比对和分析,得出以下结论。

(1) 用改进的DVSFOA调整更新位置搜索步长公式进行寻优,确认了每一次迭代移动的方向,在此基础上加大了每一只果蝇动态变步长的范围,从而使果蝇具备更强的搜索能力,可以更为迅速、准确地找到σ的最优值。通过实验结果可以看出,改进后的算法在搜索精度和速度上有明显优势,并且不易陷入局部最小值,全局搜索能力强。

(2) DVSFOA-PNN模型具有良好的自适应能力,不仅可以更快到达局部最优解,而且具备逃离局部最优的能力,从而达到更高精度的全局最优。在后续的研究中,将进一步对提高算法的初始精度和最终精度进行研究,并对该组合算法在其他领域的适用性及DVSFOA与其他优化算法的性能进行比较研究。