基于蚁群支持向量机的发电机进相能力建模评估

孙萌萌 ，郭芳芳 ，吕国栋，李 宽 ，高 嵩

（1.山东中实易通集团有限公司，山东 济南 250003；2.国网山东省电力公司电力科学研究院，山东 济南 250003）

0 引言

我国的电力负荷主要集中在东部沿海地区，矿产资源主要集中在西北地区，水利资源主要集中在西南地区，这就造成了我国电力负荷与能源聚集区的逆向分布。为了解决此类问题，特高压交直流输电得到大力发展，同时发电机组的装机容量也不断提高，造成高压输电线路相间、相对地电容变大，导致电力系统容性无功功率调节能力不足，易引起过电压或欠电压问题。为了解决欠电压问题，传统交流输电系统需要增加大量的无功补偿装置以弥补负荷高峰期的无功不足；为了解决过电压问题，需要增加大量的并联电抗器消耗过剩无功。无功补偿装置和并联电抗器虽然可有效解决过电压或欠电压问题，但不具备灵活投切的功能。当负荷低谷时，若未及时退出无功补偿装置，会造成电网无功过剩，很容易引起运行电压偏高，接近甚至高于运行电压上限，造成系统电能质量下降，严重影响电网安全稳定运行［1-3］。

系统中运行电压过高会缩短输电线路、变压器等电力设备的使用寿命，且电力设备长时间承受过电压亦可能会对其绝缘造成不可逆损坏［4-5］。鉴于以上原因，目前电网中多采用装设调相机、高压输电线路并联高抗设备、通过发电机进相运行来降低系统无功，以达到降低运行电压的目的［6-8］。发电机运行是分为迟相和进相两种方式，迟相运行时向系统发出无功功率，进相运行时吸收系统无功功率。为了弥补无功补偿装置和并联电抗器不具备灵活投切的缺点，在电网运行过程中，可通过发电机进相来降低系统运行电压，此方法具有调节平滑、不需要二次投资的优点。通过发电机进相运行降低系统运行电压具有较高的灵活性和经济性。发电机进相能力主要受定子边段铁芯和金属结构件的温度［9］、系统电压［10］、功角稳定［11-12］和系统静态稳定极限［13-14］等影响。 随着氢冷却技术的广泛应用，发电机定子端部温升已不再是主要限制因素。目前发电机进相深度的主要限制因素为系统电压、功角稳定等。专家学者针对发电机进相运行模式进行大量研究，文献［15］提出利用径向基函数神经网络 （Radial Basis Function Neural Network，RBFNN）对发电机进相能力建模的方法，最终泛化能力检验表明该模型具有收敛速度快和精度高的优点。文献［16］提出基于反向传播神经网络（Back Propagation Neural Network，BPNN）的发电机进相能力建模方法以克服传统发电机进相能力分析方法的局限性，具有较强的泛化能力。支持向量机（Support Vector Machine，SVM）［17］具有模型自由选择、良好学习能力等特点，可有效解决实际系统中非线性和高维数的问题，具有较强的泛化能力，但在实际应用中存在核函数参数、平衡因子等关键参数难以设置的情况，在一定程度上影响了SVM泛化能力。

为达到通过典型进相试验推断实际运行工况下发电机进相能力的目的，提出基于蚁群算法（Ant Colony Optimization，ACO）［18-19］的 SVM 来对发电机进相能力进行建模。通过ACO算法对SVM的参数优化，减小了SVM关键参数设置的盲目性，提高了SVM的泛化能力，即提高了发电机进行能力模型的准确性。

1 基本原理

1.1 支持向量机原理

SVM算法采用核函数映射方法，即先定义非线性映射 φ：Rn→Rm（m≥n），通过非线性映射 φ 把输入空间的数据映射到一个高维特征空间，并在此高维空间做线性回归，即此高维特征空间为线性可分。给定数据点集 G=｛（xi，yi），i=1，2，…，n｝作为输入空间，其中xi和yi分别为输入向量和输出向量，且均属于Rn，n为总采集点个数。SVM在高维特征空间的线性回归可表示为

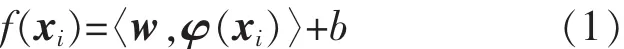
式中：w 为权向量；b 为分类阈值；φ（xi）为 xi的线性映射。其中，w和φ（xi）为m维向量，b∈R。线性回归实质就是在约束条件下做最小化规则化风险泛函如式（2）所示。

式中：xi和 yi分别为输入向量和输出向量；f（xi）为SVM在高维特征空间的线性回归；ε为误差；Lε为拉格朗日函数；l为平衡因子边界为正规化项，决定了决策函数的复杂性，通过此项可提高函数的泛化能力；常数C（C≥0）为平衡因子，起到加权系数的作用；Lε［xi，yi-f（xi）］为 ε-不敏感损失函为经验风险泛函，此泛函由惩罚函数度量，作用是训练误差项，如式（3）所示。

在给定的数据点集G中，平衡因子C的取值表现为对经验误差ε惩罚的程度，平衡因子取值较小表明对ε惩罚的较小，会造成学习机器复杂度较小、经验风险值较大的情况，这种现象被称为“欠学习”；相反，平衡因子取值较大时，会造成学习机器复杂度较大、经验风险值较小的情况，这种现象被称为“过学习”。SVM算法中支持向量的个数取决于误差ε的大小，误差ε较小时，支持向量个数多，ε-不敏感损失函数精度高；相反，误ε差较大时，支持向量个数少，ε-不敏感损失函数精度低。在误差ε的取值中，函数精度和SVM算法运算时间互为约束条件，函数精度越高，则SVM算法运算时间越长，故误差ε的取值并不是越小越好。

引入松弛变量ξi和，式（2）可改写为

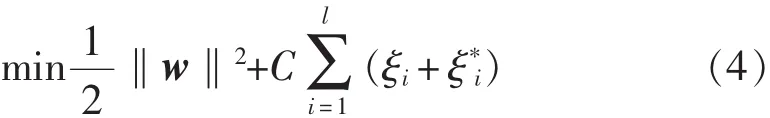
其中，约束条件如式（5）所示。

由式（4）和式（5）可知，SVM算法转化为有线性约束的二次优化问题。通过对偶定义来对式（4）和式（5）的二次优化问题求解，引入拉格朗日乘子αi和，通过拉格朗日乘子建立拉格朗日函数，并对w、b、偏导置零。 可把式（4）改写为

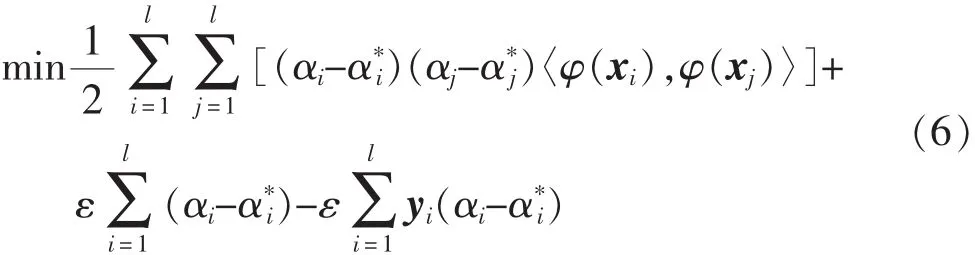
式（6）约束条件为

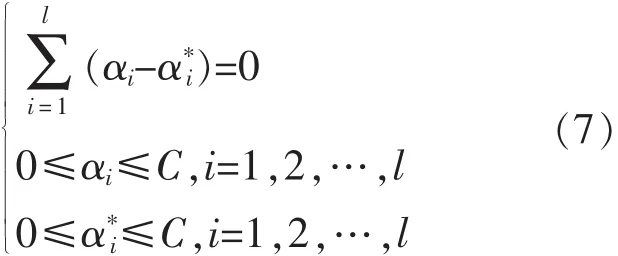
通过求解拉格朗日乘子αi和，SVM在高维特征空间的线性回归可表示为

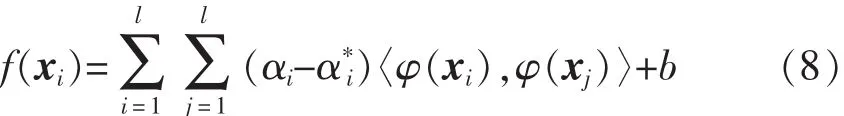
式中：〈φ（xi），φ（xj）〉为核函数，核函数参数对 SVM算法的泛化能力影响较大，在不知道非线性映射φ具体形式的情况下，可通过核函数得到线性回归方程，避免空间中的维数灾问题。

综上可知，SVM的泛化能力在一定程度上取决于平衡因子、核函数和误差的选取，这些参数在SVM高维特征空间的线性回归问题中具有决定性因素，故合理地选择SVM算法的参数可提高运算精度、缩减运算时间，即增强了SVM算法的泛化能力。鉴于蚁群算法是一种全局搜索算法，且在寻优过程中可避免过早陷入局部最优解，具有寻优效率高的优点，故提出通过ACO来对SVM算法的参数进行寻优以提高SVM的泛化能力。

1.2 蚁群算法

自然界中，蚂蚁在寻找实物的过程中，总能找到一条最优路径，降低从蚁穴到食物源所发生的时间成本，ACO就是模拟这种寻优路径提出来的一种智能算法。蚂蚁在行进的过程中，会自然释放一种化学的信息素，由此可知，信息素的浓度和最优路径成正比，即从蚁穴到食物源最优的路径信息素浓度最高。同时，信息素浓度高的路径能吸引后续蚂蚁继续通过此条路径到达食物源，故蚁群总是可以找到一条食物源到蚁穴的最短路径。蚂蚁的这种特性是一种正反馈现象，这种正反馈也加速了找到最优解的过程，且蚁群算法可通过分布式计算避免过早陷入局部最优解。

以给定数据点集G的输出向量总误差最小为目标函数

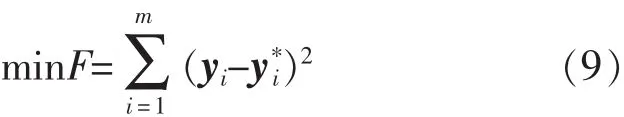
式中：yi为给定数据点集G中实际输出向量；y*i为通过SVM计算出的预测输出向量。以平衡因子、核函数和误差为约束条件，如式（10）所示。

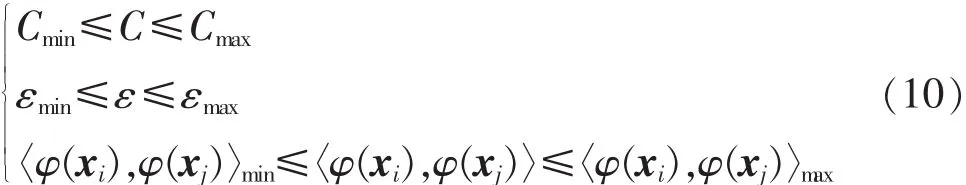
ACO算法的步骤为：

1）初始化蚁群规模和位置，计算出该规模和位置所对应的输出向量总误差F，并以信息素的大小表示误差F，F越小表明信息素越大。

2）设置蚁群算法的信息素蒸发率和移动步长，蚂蚁向信息素较大区域随机移动，并计算新位置下的信息素大小。

3）比较新位置下的信息素和上一位置下信息素的大小，以判断是否为全局最优解。若为全局最优解则寻优结束，否则执行4）。

4）根据3）位置下信息素的大小更新蚁群位置，重复 1）。

2 发电机进相能力ACO-SVM模型设计

电力系统是典型的时变非线性系统，通过发电机进相运行来调节电网中的运行电压也是一个非线性的过程，目前限制发电机进相深度的主要为系统电压、功角稳定等因素，同时这些因素也是与电力系统安全稳定运行关联最紧密的两个因素。鉴于此，提出利用ACO-SVM算法来对发电机进相能力建模，该方法兼具支持向量机算法的泛化能力和蚁群算法的快速寻优特性，以发电机有功功率和无功功率为数据点集G的输入向量，以发电机的功角和电网电压作为数据点集G的输出向量。通过ACO-SVM建模来分析发电机在某一进相运行工况下的发电机运行功角和调压效果。

2.1 算例Ⅰ

以某电厂额定功率为10 MW的发电机为例，在现场进行了不同运行深度的发电机进相试验，以确定在一定有功出力情况下的限制因素。发电机进行运行试验数据如表1所示。

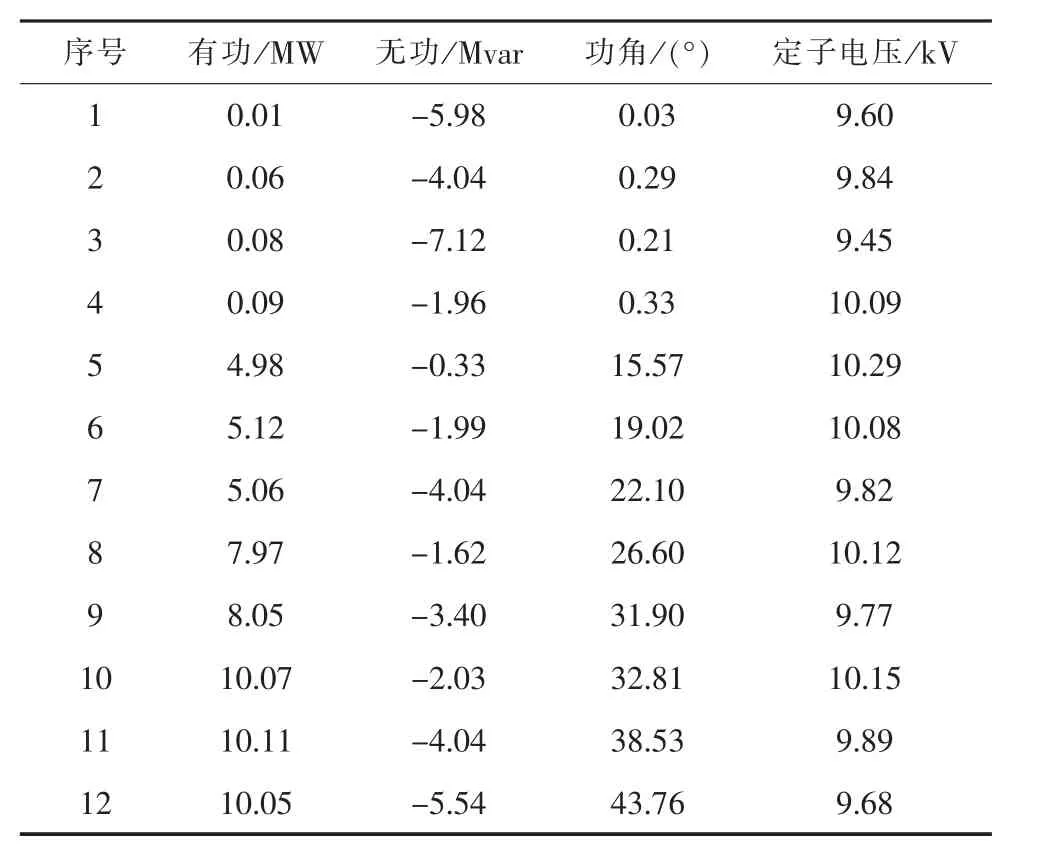
表1 10 MW发电机进相试验数据

通过发电机进相试验，得到发电机各个运行工况下进相限制因素如表2所示。

以表1所示的发电机进相试验数据作为数据点集G，采用ACO-SVM进行建模泛化，序号7和序号10的电压及功角泛化结果如表3和表4所示。

表3 10 MW发电机电压ACO-SVM泛化能力

表4 10 MW发电机功角ACO-SVM泛化能力

由表3和表4可知，在固定有功和无功情况下，实测发电机进相能力和通过ACO-SVM算法泛化结果误差较小，证明所提出采用ACO-SVM算法进行发电机进相试验建模具有可行性。

2.2 算例Ⅱ

以某电厂额定功率为300 MW的发电机为例，在现场进行了不同运行深度的发电机进相试验，以确定在一定有功出力情况下的限制因素。发电机进行运行试验数据如表5所示。

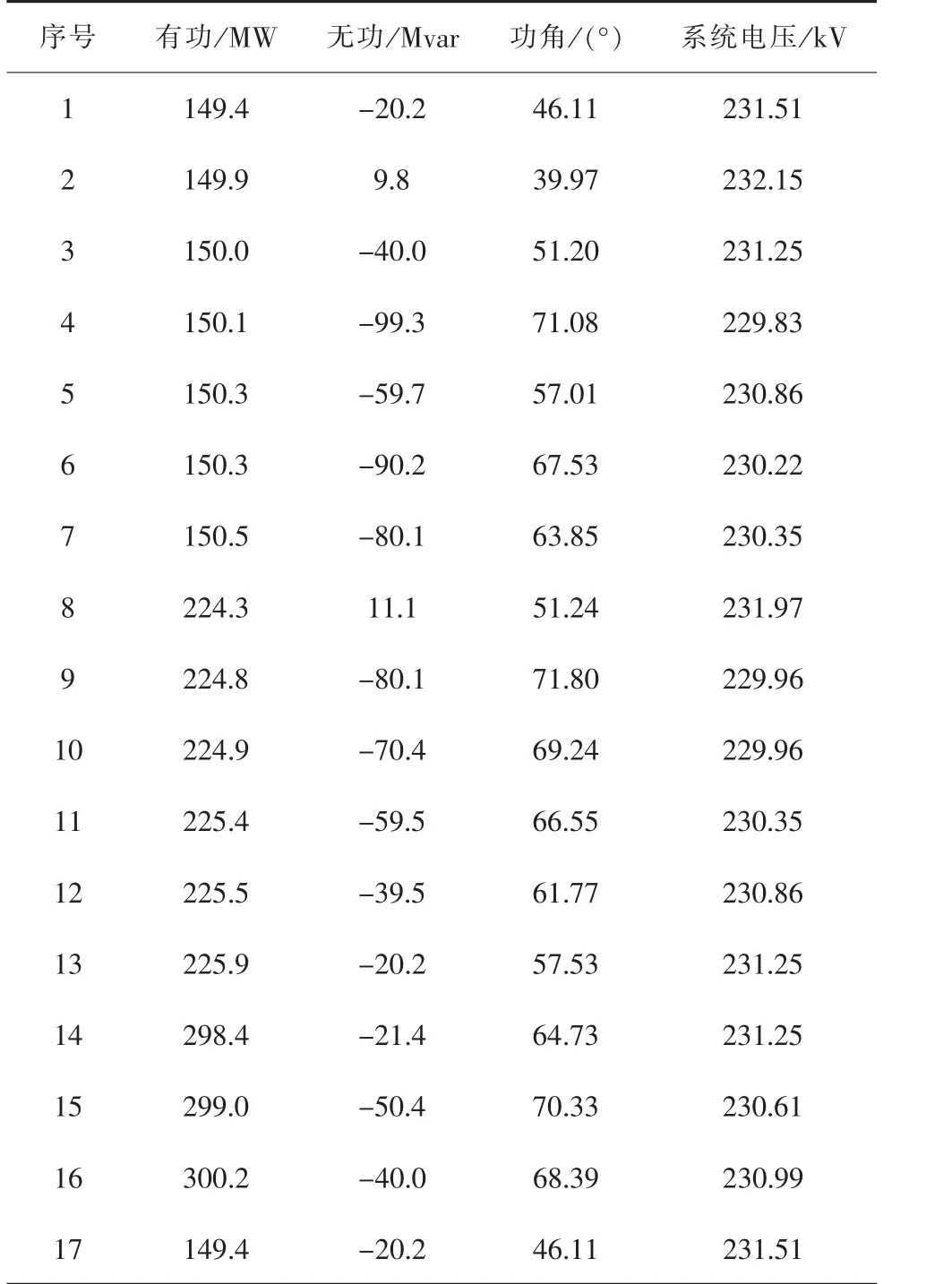
表5 300 MW发电机进相试验数据

通过发电机进相试验，得到发电机各个运行工况下进相限制因素如表6所示。

表6 300 MW发电机进相限制因素

以表5所示的发电机进相试验数据作为数据点集G，采用ACO-SVM进行建模泛化，序号7和序号12的电压及功角泛化结果如表7所示。

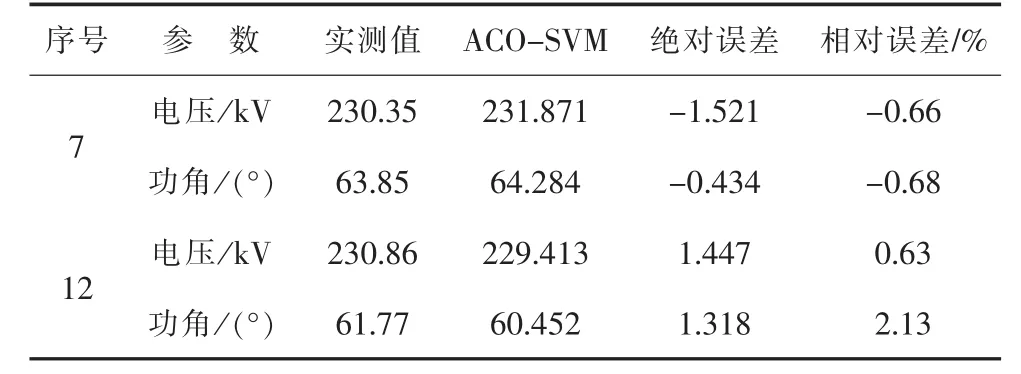
表7300 MW ACO-SVM泛化能力

由表7和表8知，在固定有功和无功情况下，实测发电机进相能力和通过ACO-SVM算法泛化结果误差较小，证明所提出采用ACO-SVM算法进行发电机进相试验建模具有可行性。

算例Ⅰ中，通过有功、无功、功角、定子电压建模，算例Ⅱ中，通过有功、无功、功角和系统电压建模，系统电压和定子电压可选，由此可证明此建模方法的灵活性。通过2个不同容量的机组来进行算法验证，2台机组进相能力限制因素分析结果有差异，可充分重说此算法的有效性。

3 结语

提出通过蚁群算法来对支持向量机中的平衡因子、核函数和误差参数进行寻优，以提高支持向量机算法的运行效率和泛化能力。并采用ACO-SVM算法来对发电机进相能力建模，分别通过10 MW和300 MW 2个发电机算例来验证ACO-SVM算法的泛化能力。通过对比发电机进相试验实测数据和ACO-SVM算法泛化结果，验证所提ACO-SVM算法建模可作为发电机进相运行时电网运行电压调节能力、发电机功角监视提供依据，具有较高的工程实用价值。