复杂型面约束的点云配准序列确定方法
林 伟,孙殿柱,李延瑞,沈江华
1(山东理工大学 机械工程学院,山东 淄博 255049)2(西安交通大学 机械工程学院,西安 710049)
E-mail:1578964766@qq.com
1 引 言
由于光学三维扫描设备的限制,每次扫描只能获取被测物体一个视角的扫描数据,为得到完整的数据模型,需要对被测物体进行多次扫描,然后将扫描得到的多视角扫描数据进行配准[1];配准是后续曲面重建的基础,也是逆向工程领域的研究重点和难点.
现有多视角扫描数据的配准方法主要为顺序配准,即按照扫描顺序将所获得的扫描数据进行逐次配准.其中最具有代表性的为Chen等[2]提出的全局刚性配准算法,该方法首先将其中一个视角的扫描数据所在的坐标系确定为基准坐标系,然后根据顺序依次添加新的扫描数据进行配准,直到获得完整的数据模型.Bergevin等[3]将扫描数据先进行两两配准,并迭代此过程直到配准误差被均匀分配到每次配准过程中,避免了配准误差的累积但配准效率大大降低.Mateo等[4]在通过期望最大化算法将多视图点云配准问题嵌入到贝叶斯框架中,同时考虑双视图的对应关系及噪声影响,最后进行后验判断,提高了配准的整体精度及稳健性.Evangelidis等[5]提出一种期望最大化算法,该方法将扫描数据中的每个点都视为从高斯混合模型中抽取的样本点,从而将多视角扫描数据的配准问题转化为聚类分析问题,通过期望最大化方法计算计算扫描数据间的变换矩阵,提高了整体的配准精度.徐思雨等[6]提出一种逐步求精的多视角扫描数据配准方法,首先构建初始配准模型,然后按照双视角配准算法计算配准参数并调整配准模型,以便求解后续配准参数,通过迭代求解配准参数并调整配准模型可最终实现全局配准.
随着三维扫描设备精度的提高,单次扫描所获得点云的密度越来越大,点云数据量急剧增多,利用顺序配准不但配准效率较低且会产生误差累计现象,严重影响整体配准精度.因此,为实现大数据量多视角点云的快速配准,本文提出一种三维扫描系统中复杂型面约束的多视角点云配准序列确定方法,通过主成分分析度量点云的局部形貌平坦程度,分割平坦区域点云并提取距离质心最近点作为保留点进行自适应简化;结合平坦区域子集的样点规模及子集中所有样点到拟合平面的偏差均值量化待配准点云的形貌复杂度,并通过形貌复杂度确定配准序列.实验结果表明,本文算法能够在维持点云原始形貌的情况下有效简化待配准点云,在多视角点云配准过程中可避免累积误差的产生,有效提高多视角点云的整体配准精度.
2 形貌自适应聚类简化
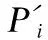
为保证点云配准精度,对参与配准的任一点云P的简化应当在尽量维持其原始形貌的前提下进行.如果能够将P分割为足够多的子集,且其中任一子集来自P上足够平坦的子域,那么每个子集只需贡献少量采样点,由这些采样点构成的P′即可作为点云的保形简化结果.对于点云P,设C={C1,C2,…,CK}为其分割结果,即Ci∈P,且Ci∩Cj=φ,i={1,2,…,K},j={1,2,…,K},i≠j,采用k均值聚类算法[7]可以获得C,且能保证任一子集Ci来自P的一个子域.
对于P中的任意一点xi,利用k均值聚类算法将其归类到任意子集的过程可表示为i=A(xi).要保证xi会被正确的归类到Ck中而不是其他的子集,需要衡量任意两个点xi与xj的相异度.d(xi,xj).d(xi,xj)的值越大,表示点xi与xj越相异,反之则表示二者越相似.若xi与Ck中所有点的相异度的总和小于其他子集,便可以断定xi属于子集Ck.将P分割为{C1,C2,…,CK}的过程,本质上是令函数:
(1)
最小化,即令每个子集内的点之间的相异度之和最小.A(xi)定义为:
(2)
其中ck为Ck的中心点即Ck中所有点的均值点.
Ck在原曲面上对应区域的平坦程度可基于主元分析法[8]予以量化.设Ck={xi|i=1,2,…,ni},则构造Ck的协方差矩阵为:
(3)
(4)
对C(Ck)进行特征值分解:
(5)
设最小特征值为λ1,对应的特征向量v1即为Ck的拟合平面的法向量,λ1为Ck中的样点在v1方向上的偏离程度,因此可用λ1来度量Ck的平坦程度,将其定义为平坦度.显然,可通过设定平坦度阈值ζ来判定Ck的形貌平坦与否,即若λ1<ζ,可将Ck的形貌视为平坦,否则为非平坦.因此,基于ζ可实现P中平坦区域与特征区域的划分.
若P的分割结果中存在子集Ck,该子集在原曲面上对应区域的平坦度不足,即Ck所对应λ1>ζ,可继续采用k均值聚类算法对Ck进行分割.由此对P可形成一个递归分割过程,使得最终所得分割结果中任何一个子集在原曲面上对应区域的平坦度都满足要求,这种递归分割方法称为多层形貌分割.
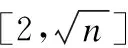
1)输入待简化数据P.
2)对P进行聚类数目为2的k均值聚类直到聚类误差平方和E收敛,获得C1={C1,C2}.
3)k←1,r←1.
4)根据式(3)-式(5)计算Ck的平坦度λ1.
5)当λ1<ζ跳过,当λ1≥ζ时,则将Ck作为输入数据,重复步骤2),获得Cr+1.
6)k←k+1.
7)重复步骤4)-步骤6),直至k=2.
8)r←r+1.
9)重复步骤4)-步骤8),直到所有子集均有λ1<ζ,获得二叉树结构的多层形貌分割域F.
10)对于最底层叶结点子集计算质心并析取距离质心最近点作为保留点,合并保留点得到P的简化点集P′.
步骤2)中的聚类误差平方和可用以下函数度量:
(6)
其中xij表示第k个子集的第j个点,ck为Ck的子集中心,nk为Ck中的样点数量.
3 点云形貌复杂度
对于多视角点云{P1,P2,…,PN},现有的初始配准算法大多通过对P检测特征点,然后通过计算相应的特征描述符来匹配特征点进行配准.例如Rusu等[9]提出的快速点特征直方图(Fast Point Feature Histograms,FPFH),即是通过计算特征点与其邻域点之间的空间几何关系,构造一个33维的直方图对特征点进行描述,通过比较直方图之间的差异完成特征点的匹配.而P′中的样点大多位于特征区域,对于其中任一点xm,其构造的特征描述符相较于平坦区域样点更具有识别性,因此特征区域相较于平坦区域更有助于点云初始配准,所以可通过量化待配准点云所包含的特征情况来提高点云配准效率.
设F={C1,C2,…,Cm}为待配准点云P的多层形貌分割域.P包含越多特征,其形貌越复杂,需要分割的次数越多,F的层数越大,其最下层数所对应的叶结点中的样点规模ni越小,因此ni在一定程度上可反映点云形貌复杂度.
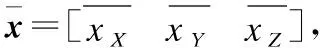
(7)
计算P中全部样点到拟合平面的偏差距离,则其偏差均值χ(P)可有效度量P的形貌复杂程度.
基于上述分析,定义点云形貌复杂度为φ,其计算公式为:
(8)
其中χ(P)为:
(9)
联立以上方程可得:
(10)
点云复杂度φ综合考虑了叶结点子集样点规模ni和偏差均值χ(P),对待配准点云P完整形貌复杂度的表达更加的合理、准确.
4 确定配准序列
点云形貌复杂度较大的待配准点云其形貌更为复杂,包含更多的特征,在初始配准过程中可对特征点构造高识别度的特征描述符,有利于保证配准的正确性,不易陷入局部最优,因此可根据φ值确定点云配准序列.


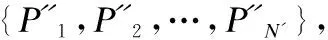
1)输入多视角点云{P1,P2,…,PN},i←1.
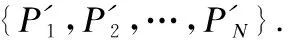
4)i←i+1.
5)重复步骤3)-步骤4),直至i=N.
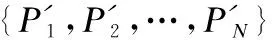

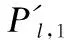

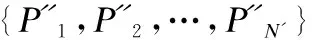
5 实验分析
为验证本文算法的有效性,以下实验均在硬件配置为Inter(R)Xeon CPU 2.5GHz,4GB内存,操作系统为GNU/Linux,测试程序为C++的环境中进行.实验数据采用dawei点云模型和train点云模型,其中dawei点云模型由12个视角点云组成,将其分别命名为D1-D12,train点云模型由9个视角点云组成,将其分别命名为T1-T9,如图1所示.
本文算法在计算多视角点云形貌复杂度之前需对其进行简化[11],以D1、T1为例,简化结果如图2所示.可以看出简化后的点云特征区域样本点相较于平坦区域更为密集,可在减少样本点数量的同时有效维持原始形貌.
统计实验数据的形貌复杂度,其结果如表1所示.可以看出,在D1-D12中D11的形貌复杂度最大,在T1-T9中T4的形貌复杂度最大,因此分别将其作为第一轮配准序列中的固定点云,并根据本文算法确定其配准序列.
为验证本文算法的有效性,分别采用顺序配准算法、文献[4]算法和本文算法进行配准,配准精度如表2所示,其中均匀误差表示相邻两视角误差均值,首尾误差表示第一固定点云与最后添加点云之间的误差,配准结果如图3所示,可以看出,本文算法与顺序配准算法相比能够有效降低首尾误差[12,13],与文献[4]算法配准精度类似,但由于本文使用简化后的点云进行配准,可有效减少配准过程中的计算量,因此配准效率高于文献[4]算法.

图1 实验数据Fig.1 Experimental data

图2 简化结果Fig.2 Simplified results
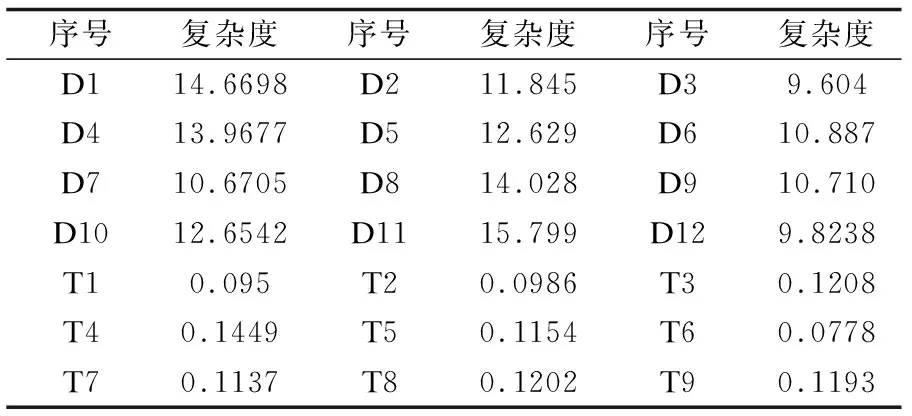
表1 实验数据形貌复杂度Table 1 Shape complexity of experimental data

表2 实验数据配准精度(MSE/mm)Table 2 Registration accuracy of experimental data
调整实验数据样点规模,统计配准所用时间如图4所示.可以看出,相较于顺序配准算法与文献[4]算法,本文算法可有效缩短点云时间,且随着实验数据中样点数量的增加,与其他两种配准算法之间的差距越来越大.
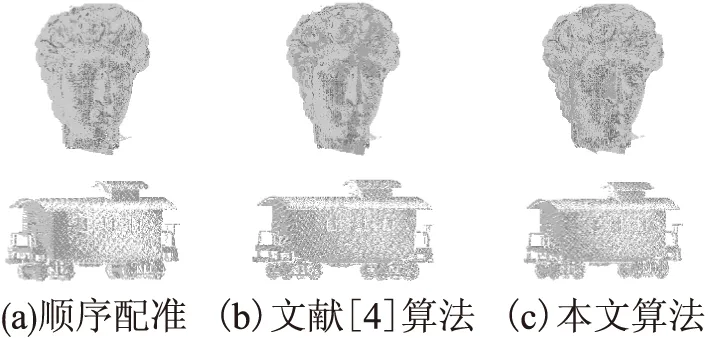
图3 配准结果Fig.3 Registration results
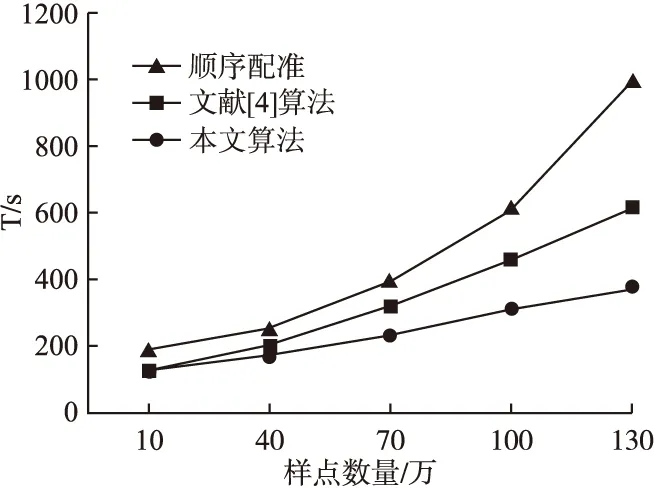
图4 配准时间对比Fig.4 Registration time comparison
6 结 论
针对多视角点云采用顺序序列配准会产生较大的累计误差的问题,提出一种形貌复杂度约束的点云配准序列确定方法.该方法具有以下特点:
1)通过主成分分析判定点云形貌,基于形貌约束将点云进行迭代分割并提取每个子集中距离质心最近的样点作为保留点,可实现点云的保形简化.
2)对子集进行拟合平面并计算子集中所有样点到平面的偏差均值,结合子集样点规模计算点云的形貌复杂度,可有效刻画待配准点云的整体形貌的复杂程度.
3)基于待配准点云的形貌复杂度确定固定点云及浮动点云,进而确定点云配准序列,可将配准误差分布于每轮配准之中,避免了最终累计误差的产生.

