基于随机图的复杂网络建模方法研究
李 姝,邵志香,于金刚
1(沈阳理工大学 装备工程学院,沈阳 110159)2(页岩油气富集机理与有效开发国家重点实验室,北京 100101)3(中国石化石油工程技术研究院,北京 100101)4(中国科学院 沈阳计算技术研究所,沈阳 110168)
E-mail:lishucx@163.com
1 引 言
近年来,复杂网络系统的研究在不同领域发挥着越来越重要的作用.随着计算机与互联网技术的蓬勃发展,建立一个满足接近于真实互联网通信需求及最短通信链路的复杂网络模型,以此为基础进行复杂网络的研究是十分有意义的.由于复杂网络分布错综复杂,且网络传输中受网络承载量及传输质量等诸多因素的限制,虽然表面上复杂网络的传输路径是随机的,但这并不意味着复杂网络毫无规律可循.有研究表明,很多网络具有小世界性质[1,2],即从原点节点到目的节点的访问路径存在一条“相对固定”的最短通信链路.这里的“相对固定”是根据一定的发生概率而言的,即从源节点到目的节点的通信链路是存在一定的访问概率的,这说明人们访问某个站点或者服务器的通信链路也是相对固定的[3,4].
根据上述研究,有研究者提出利用随机图理论可以生成与真实网络访问拓扑结构具有高相似度的随机图网络模型,能够更好的模拟与研究复杂网络的通信[5,6].基于此,本文在随机图理论的基础上,提出了基于随机图的树型网络仿真模型k-RGN,该网络模型是一种充分考虑连接链路权重,且服从指数分布的随机网络模型.通过网络模型的对比实验,验证了k-RGN随机网络模型在带宽、丢包率、时延、时延抖动、跳数等多参数指标规划中,具有最优的网络性能.
2 随机图理论与随机图模型
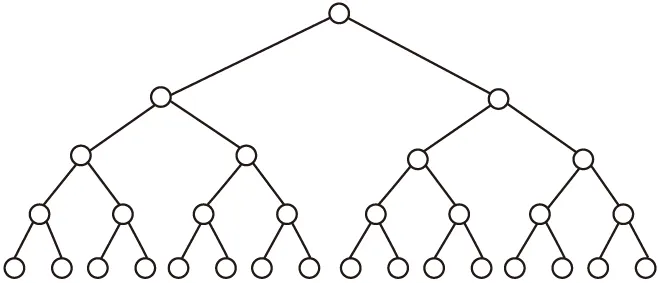
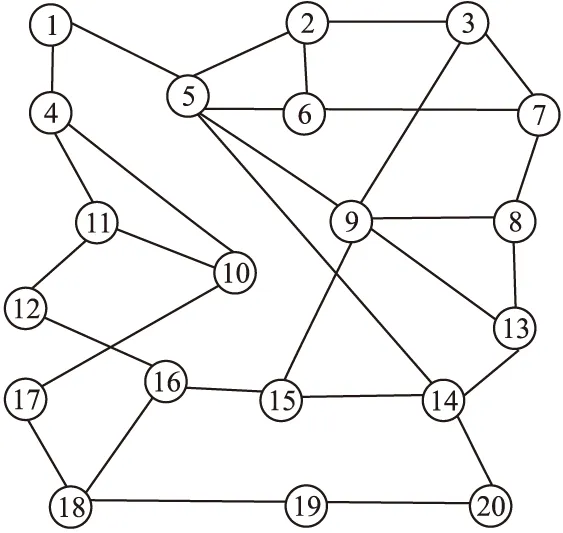
设某个概率空间中的每一节点都看作是一个图,则称这些图为随机图[7,8].其中随机图Gp(n)定义:概率空间由V={1,2,…,n}为节点的n个图集组成.其中n个节点是可区别的,即每个图被认为是不同的图,出现概率p满足0 随机图Gp(n)最广泛的应用之一是建立随机网络,研究者们一直以来致力于研究出一种被广泛用来生成复杂网络的随机图模型方法,达到生成具有指定度序列[9]或者具有指定幂律分布的复杂网络.用随机图生成随机网络模型,其建模方法如下[10,11]: 给随机图Gp(n)中的每个节点都附加一个顶点权重w,则节点i与节点j之间存在一条边的概率为: (1) 将顶点赋予权重,可以使得随机图模型更好的适应于网络的实际分布.节点的权重越大,表明该节点与其他节点相连的概率就越大,我们通过选取合适的节点权重,来构建一个更贴近于实际网络的随机模型.假设我们构造了一个包含两种不同类型节点的网络,第一类节点的权重为w1,第二类节点的权重记作w2,n1与n2分别表示第一类节点与第二类节点的个数.即: ln=n1w1+n2w2 (2) (3) 由式(3)可知,第一类型节点的期望度数趋近于w1.同理可推,第二类节点的期望度数趋近于w2. 由上可知,基于随机图的网络结构高度依赖于顶点权重,在实际网络中,顶点的权重可以设置固定值,或更加复杂的随机变量序列.为了研究顶点权重的经验性质,我们定义顶点权重的经验分布函数: (4) 可以将Fn(x)看成随机选取节点权重的分布函数,在应用中,通常假设顶点权重服从正则化条件. 根据随机图理论在随机网络中的建模可知,虽然随机网络模型与物理上的网络拓扑结构并不一致,但它与实际的网络访问结构或者路由连接链路可以有很好的吻合.然而,随着随机图理论应用于通信网络建模的研究深入,有研究表明[12-14],广义随机网络模型只适合于普通简单规模的网络访问模型,对于大型复杂通信网络,其网络模型表现并不理想. 鉴于此,本文在随机图理论的基础上,提出一种基于随机图的k-叉树网络模型(k-RGN),使得随机图Gp(n)的网络模型服从于指数分布,进而适用于大型复杂通信网络结构;此外,k-RGN网络模型充分考虑连接链路的权重问题,使随机网络模型更适用于实际网络访问需求和最短访问路径的复杂网络. 设一棵k叉树由一个源点和N个节点组成,树深度D等于从源点到节点的跳数,m为随机选取的遍历节点个数,k为树的分枝数,k叉树网络模型如图1所示.在一棵k叉树中,节点的总数满足下式: (5) 由公式(5)可知,N服从于kD,记N~kD. 我的爸爸还是一个幽默搞笑的人。有一次,他无意间捞到了一只青蛙,“看!这只青……”他刚说到这里,那只青蛙就回头看了看他,“扑通”一声跳进了水里,弄得他满脸都是泥水,就像是一只“大青蛙”。我看了一眼被泥水溅成“大花脸”的爸爸,“扑哧”一声笑了出来。 图1 k-叉树网络模型k=2,N=21,D=4Fig.1 k-tree network model k=2,N=21,D=4 建立k-RGN网络模型,需要考虑两点问题:1)随机图网络的连通性,即随机生成树应遍历所有节点,并且确保每个节点都是双连通的;2)随机链路的产生,即我们如何让产生的随机网络更接近于真实网络的连接状况.具体步骤如下: 1)产生随机节点.首先建立笛卡尔坐标系xoy,将坐标系以整数最小单位划分成网格(可以将网格单位设为1),利用整数随机发生器产生随机节点,使随机节点均落在网络上;然后分别检查产生节点的横纵坐标间距,删除掉间距小于5的随机节点,并重新生成节点,直至满足间距为止; 2)产生随机链路.网络的随机节点产生后,接下来在这些节点中建立随机链路,这里的“随机链路”并非是完全的随机,这里我们模拟与实际网络访问链路最接近的连接方式,构建一个连通的随机网络. 在实际的网络通信中,通常是节点间距离越大,节点间建立连接的可能性越小,但我们并不能简单地以距离作为节点间连接的依据,这与实际需求中的网络通讯结构并非一致.本文基于随机图理论,将节点间的距离设为连接权重,并带入节点间存在链路的概率P中.连接概率P与节点间的距离有关,建立节点间连接概率P函数如下: (6) P(u,v)是节点u和节点v之间存在连接的概率,d(u,v)是它们之间的距离,L是网络节点间可能的最大距离之和,权重参数w是控制远程连接和本地连接所占的比重,长连接的比重越大,w取值越大.值得说明,参数w应该服从公式(4)经验分布函数Fn(x),这里为方便计算,我们设w取值为0到1.参数γ调节网络的平均节点度数,γ越大,网络平均节点度数越多. 3)检查网络连通性.使用式(6)产生的随机网络在大量节点时,不能保证网络的连通性.为了纠正网络的非连通性,我们再检查网络中的每个节点的连接度数,如节点的连接度数为1时,将该节点与网络中的其他节点随机产生一条链路.经过反复处理,产生的随机网络一定是有双连接的连通网络. 图2 k-RGN网络模型Gp(20)Fig.2 k-RGN network model Gp(20) 实验选取200*200的笛卡尔坐标,横、纵坐标的随机数在0到200之间产生,坐标轴最小刻度单位为1.设随机网络的节点个数N=20,权重参数w=0.16,调节系数γ=3.7.实验任意选取节点u和节点v,根据公式(6)计算它们之间可能存在连接的概率P(u,v),在0到Rmax之间产生一个均匀分布的随机数Ri,如果随机数Ri的概率Pi满足于公式(7),则节点u和节点v之间存在连接,否则不存在连接.反复随机选取各节点,产生随机连接.每当增加一条连接时,需要进行判断是否达到了平均节点度数,若己经达到,则停止.如图2所示选取节点数为20个时,产生的随机网络模型. Pi=Ri/Rmax (7) 本文基于随机图原理,建立了k-RGN网络仿真模型,其研究意义在于预测k-RGN网络仿真模型在实际通信的复杂网络中所表现的连接状况及网络性能,为拓展复杂网络理论研究和验证实际应用效果提供依据.通常用以描述网络综合性能的指标包括:带宽、时延、时延抖动、丢包率和跳数等. 时延是指一个报文或分组从一个网络的一端传到另一端所需要的时间,时延等于发送时延,处理时延,传播时延与排队时延之和.这里我们只计算传播时延,即从一个节点进入下一节点所需的时间间隔.设tij是i节点到j节点之间的时延. 时延抖动是指信息通过节点的最大与最小时间延迟差.设sij是i节点到j节点之间的时延抖动. 丢包率是指在链路的传输过程中所丢失的包数与传输包的总数之比,它体现链路的可靠性.设lij是i节点到j节点之间的丢包率. 跳数是指路径所经过的链路数(即从原点到目的节点所经过的节点数).设hij是i节点到第j节点之间的跳数. 在k-RGN网络模型中,从节点i到节点j假设存在k条链路,则从节点i到节点j的总带宽为: (8) 从节点i到节点j的总时延为: (9) 从节点i到节点j的总时延抖动为: (10) 从节点i到节点j的总丢包率为: (11) 从节点i到节点j的总跳数率为: (12) 实验在最短路径算法(Dijkstra算法)生成的网络模型,与基于随机图的k-RGN网络模型中进行,比较这两种网络模型的网络性能.实验分别选取,节点数n=20,60,100.对选取的各个节点数所限定产生的网络规模分别为3*n个网络连接单元.实验分别选取0.1*n组,0.2*n组,0.3*n组随机节点进行通信仿真,每组网络独立重复试验20次,最后求取各参数均值.选取节点个数100时,网络性能参数对比如表1所示. 表1 节点数100两种模型的网络性能参数对比Table 1 Comparison of network performance parametersat 100 nodes 通过对比试验可知,在实验选取节点个数为100个时,基于随机图的k-RGN的网络仿真模型的网络平均带宽、时延、抖动时延、丢包率、跳数等性能参数均优于由Dijkstra算法生成的网络模型.实验结果说明,基于随机图的k-RGN的网络仿真模型在多个网络通信节点数的复杂网络中,仍然表现出较好的网络综合性能. 本文在随机图理论的基础上,结合k-叉树模型提出了基于随机图的树型网络仿真模型k-RGN.该网络模型是通过引入连接权重w,将复杂网络模型更接近于实际网络访问的通信链路;此外k-RGN网络仿真模型是服从指数分布的随机网络模型,其网络节点度值符合平均值为np的泊松分布,且存在最短的连接链路d.最后通过模型的对比实验分析,验证了k-RGN随机网络模型在平均带宽、丢包率、时延、时延抖动、跳数等多参数指标规划中,均优于普通路由算法建立的网络模型.基于随机图k-RGN网络模型具有很好的网络综合性能,适用于复杂网络建模.

3 基于随机图的k-叉树网络模型
4 随机图k-RGN网络模型的网络性能分析

5 结 论

