一种新型贝叶斯模型的网络风险评估方法
王 辉,张 娟,赵 雅,刘 琨,冯文峰
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
E-mail:1497222781@qq.com
1 引 言
随着计算机网络的快速发展,网络攻击发生地越来越频繁,导致网络安全问题也越来越严重.网络攻击之所以不断发生,最主要的原因在于计算机系统中存在漏洞[1],例如比较有名的 “WannaCry勒索病毒”攻击事件就是利用windows不同版本存在的漏洞实施攻击,给国家、企业、个人带来了不同程度的经济损失[2].中国信息安全中心公布的数据表明,截止到2017年,网络中又新增了15,955个软硬件漏洞,漏洞数量的增多又进而加剧了网络安全隐患[3].网络安全风险评估作为主动防御技术之一,它可以帮助网络管理员发现潜在的网络漏洞和威胁,从而降低网络风险.
2 相关研究
近年来,国内外学者对网络安全风险评估进行了研究,并提出了一些基于不同观点的评估方法.吴泓润等[4]设计了基于攻击代价的网络攻击选择模型,通过对攻击代价分析,找出成功概率较大的网络攻击,并给出相应的防护措施,降低了网络安全风险,但该方法忽略了实际应用中攻击者还会考虑攻击收益.FuxiongSun等[5]将马尔可夫链和攻击图结合对网络进行风险评估时,提出根据漏洞信息是否发布,是否有对应的攻击方法和攻击工具量化原子攻击成功概率,并在此基础上计算节点风险值;胡浩等[6]提出将攻击图转换为吸收马尔可夫链,使用CVSS漏洞评分标准量化马尔可夫链中节点状态转移概率,进而计算各节点的概率;上述的方法具有一定的可行性,但在计算节点概率时,忽略了攻击者是智能的决策体,还会考虑攻击代价和攻击收益.同时文献[4-6]由于没有考虑网络中检测到的攻击事件对节点概率的影响,只能静态地评估网络风险,无法动态评估.
Xie等[7]利用贝叶斯网络分析网络安全时,对攻击事件加以考虑,但该方法没有进一步对观察到攻击事件的节点进行后验概率的计算.Poolsappasit等[8]将贝叶斯网络中观察到的节点状态作为攻击证据,进而计算网络中节点后验概率,从而动态评估网络风险,给网络管理员实时地掌握网络安全状况提供了便利.
陈小军等[9]利用观察到的攻击事件去对某步攻击发生的概率进行推导,但推导过程中只讨论了某节点观察到的攻击事件对该节点后验概率的影响,忽略了与该节点有关联的其它节点的后验概率会受该节点后验概率的影响; Gao Ni等[10]通过贝叶斯攻击图对网络进行风险评估时全面考虑了攻击事件对相关节点后验概率的影响,但在计算节点概率时,没有进一步分析攻击代价和攻击收益对概率的影响.马春光等[11]利用贝叶斯攻击图对网络进行动态评估时,从攻击压力、未知威胁等方面对节点概率进行了量化,提高了评估结果的准确性,但在计算节点概率时忽略了节点间关系为“或”的状况.随着网络中的资源节点增加时,陈小军、Gao Ni、马春光利用贝叶斯推理计算后验概率时的时间复杂度可能会呈指数级增长,不利于及时评估网络风险.
基于上述分析,本文做了如下工作:
(a)对攻击代价和攻击收益分析,引入攻击效能变量,并结合漏洞利用成功率给出原子攻击成功概率的公式,由此进一步计算节点概率,从而对网络风险进行静态评估;
(b)给出节点删除次序算法(NDO_Alg)确定消元顺序,将贝叶斯攻击图转换为相应的团树,然后结合检测到的攻击事件,利用团树传播算法计算后验概率,对网络风险进行动态评估.
3 贝叶斯攻击图模型
攻击图能清晰地描述网络中各个脆弱性之间的潜在关联,为网络风险评估提供了便利[12].使用攻击图进行风险评估时,由于攻击行为的不确定性,增加了网络安全风险评估的难度和影响了风险评估的准确性,而贝叶斯网络在解决关联性和不确定性导致的问题方面有较大优势[13,14].因此本文通过将贝叶斯和攻击图结合,构造贝叶斯攻击图对目标网络建模.
定义1.(贝叶斯攻击图)BSNAG={S,E,P,F,Ppre,O,Ppos}是有向无环图,各参数定义如下:
a)S={si|si∈Sb∪Sm∪St,i=1,2,…,N}表示资源状态节点集合.其中,si具有伯努利随机变量的性质,si=0表示资源未被攻击者占有,si=1表示资源被攻击者占有.
Sb={sj∈S|∃si∈S,si∈Pa(sj)}为初始的资源状态节点集合,Pa(sj)为sj的父节点集合;Sm={sj∈S|∃si,sk∈S,si∈Pa(sj)∧sj∈Pa(sk)}为中间资源状态节点集合;St={si∈S|∃sj∈S,si∈Pa(sj)}为目标资源状态节点集合.
b)E={ei→j|i=1,2,…,N,j=1,2,…,N}表示资源状态节点间的有向边集合也是原子攻击集合.E⊆S×S,若∃si,sj∈S,si∈Pa(sj),则有ei→j=
c)P={P(ei→j)|i=1,2,…,N,j=1,2,…,N}表示原子攻击成功概率集合.∀P(ei→j)∈P为有向边E上的权值;
d)F={And,Or}表示父节点间的依赖关系集合.∀si∈Sm∪St,∃fi∈F表示si父节点间的依赖关系;
e)Ppre表示资源状态节点的先验概率;
f)O={oi→j|i=1,2,…,N,j=1,2,…,N}表示检测到的攻击证据集合.其中,攻击证据oi→j表示入侵检测系统检测到原子攻击ei→j;
g)Ppos表示资源状态节点的后验概率,即结合检测到的攻击证据,动态更新后的资源状态节点概率;
4 原子攻击成功概率分析
原子攻击的发生与网络中存在的资源(安全缺陷)有关,多数学者对原子攻击成功概率量化时,通常用漏洞自身利用成功概率表示,往往忽略攻击者是理智的决策体,在对网络中的某漏洞实施攻击时,不仅会考虑漏洞利用成功概率,还会考虑攻击此漏洞获取的收益和付出的成本,因此本文利用上述三个指标计算原子攻击成功概率.
4.1 漏洞利用成功概率分析
漏洞利用成功概率可以用CVSS评分系统中基础(Base)评估部分的攻击矢量(Attack Vector,AV),攻击复杂度(Attack Complexity,AC),身份认证(Authentication,AU)三个指标衡量[15],指标对应的属性评分标准如表1所示.

表1 属性评分标准Tabel 1 Attribute scoring standard
根据CVSS评分系统,漏洞vi的利用成功概率量化公式:
P0(vi)=2×AV×AC×AU
(1)
4.2 原子攻击收益分析
定义2.原子攻击收益(AttackProfit,AProfit):是指攻击者实施一次原子攻击时,获取的利益.本文用资源损失量化原子攻击收益.
定义3.资源损失(Resource Loss,RL):表示某资源受到原子攻击后遭受的损失,本文借鉴文献[16]量化资源损失的思想,从攻击威胁度、资源重要性、资源安全属性三方面对资源损失进行描述.
定义4.攻击威胁度(Attack Threat,AT):表示攻击者实施的攻击对目标资源造成的危害程度.攻击威胁度量化如表2所示.
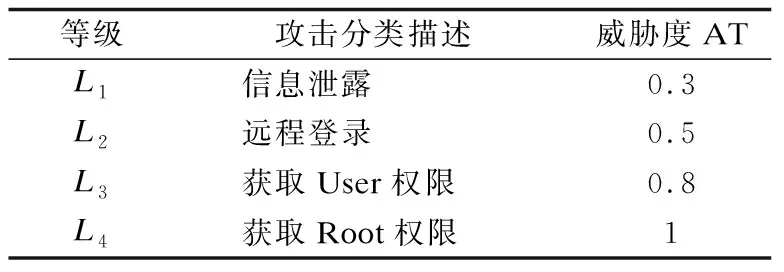
表2 攻击威胁度量化Tabel 2 Attack threat metrics
通常用CVSS评分系统中的保密性(Confidentiality,C)、完整性(Integrity,I)、可用性(Availability,A)三个指标表示资源的安全属性.不同攻击对安全属性中的三个指标造成的危害不同,用(Lc,Li,La)表示对三个指标的不同偏重,且Lc+Li+La=1,例如(0,1,0)表示针对安全属性的完整性实施攻击.
定义5.资源重要性(Resource Importance,RI):表示目标节点在网络中的重要程度,用high、mid、low三个等级表示,本文给出了典型资源的重要性量化标准,如表3所示.

表3 资源重要性量化标准Tabel 3 Resource importance quantification standard
资源重要性对安全属性的三个指标有不同的偏重(Rc,Ri,Ra),且Rc+Ri+Ra=1,偏重量化标准如表4所示.

表4 安全属性偏重量化标准Tabel 4 Safety attribute partial weighting standard
结合攻击威胁度,资源重要性和安全属性的分析,给出资源损失的计算公式:
RL(ei→j)=AT×RI×(Li×Ri+Lc×Rc+La×Ra)
(2)
由定义2可知,原子攻击收益AProfit(ei→j)为:
AProfit(ei→j)=RL(ei→j)
(3)
4.3 原子攻击成本分析
定义6.原子攻击成本(Attack Cost,ACost):表示攻击者进行一次原子攻击时,需要付出的代价,原子攻击成本由操作成本和风险成本两方面构成.
文献[17]给出了原子攻击ei→j的操作成本的计算公式:
Cost(ei→j)operation=α×Cost(meta-operations)
+β×Cost(sequence)
(4)
其中,Cost(meta-operations)表示元操作成本,Cost(sequence)表示操作序列成本.
在实施攻击的过程中,攻击者除了付出操作成本外,还需承担风险成本,风险成本由风险系数、攻击者拥有的攻击经验共同决定.风险系数θ表示攻击者发动攻击的过程中被网络安全员发现的可能性.目标节点在网络中的关键性M(vj)对θ有影响,目标节点在网络中越关键,攻击者对该目标节点发动攻击的可能性越大,相应地该攻击行为被管理员发现的可能性也越大.
通常目标节点被攻陷后给网络带来的影响越大,认为该目标节点在网络中所处的位置越关键.利用CVSS[18]评分标准计算目标节点的影响性:
lmpact(vj)=10.41*[1-(1-I)*(1-A)*(1-C)]
(5)
由公式(5)进一步给出计算目标节点对应的关键性,公式如下:
(6)
其中,N表示网络中的目标节点个数.
攻击者实施攻击的复杂度δ(ei→j)对θ也有影响,攻击对应的复杂度越大,攻击者越容易攻陷目标节点,相应地该攻击行为被检测到的可能性也越大,攻击复杂度的量化[5]如表5所示.

表5 攻击复杂度量化标准Tabel 5 Attack complex metrics
基于上述分析,风险系数θ的公式如下所示:
θ(ei→j)=M(vj)×δ(ei→j)
(7)
攻击者是理智的决策体,随着攻击者对某一目标节点攻击次数的增加,攻击者的攻击经验会相应增加,攻击者再对该目标节点实施攻击时,付出的成本会相应减少.
结合风险系数和攻击经验的分析,给出原子攻击ei→j的风险成本公式:
Cost(ei→j)risk=η(ei→j)n-1×θ(ei→j)
(8)
其中,n为攻击者对某一目标节点实施攻击的次数,η(ei→j)的具体取值由专家经验根据网络实际场景给出.
结合操作成本和风险成本的分析,本文给出原子攻击成本的计算公式:
ACost(ei→j)=γ×Cost(ei→j)risk+λ×Cost(ei→j)operation
(9)
其中,γ,λ分别为风险成本、操作成本对应的权重,且γ+λ=1.
4.4 原子攻击效能分析
定义7.原子攻击效能(Attack Efficacy,AE):表示攻击者对原子攻击的认可度,认可度越高,攻击者越倾向于实施此攻击.
攻击者实施攻击前会评判攻击付出的代价和获取的收益,根据代价收益比判断攻击效能.比值越高,表明代价越大或收益越小,对应的攻击效能越低;反之对应的攻击效能越高.
根据公式(3)和公式(9),实施原子攻击的代价收益比ε(ei→j)为:
(10)
依据上述分析,结合公式(10),给出攻击者对原子攻击ei→j的认可度,即攻击效能AE(ei→j)为:
(11)
若ε(ei→j)≥1,说明攻击代价大于等于攻击收益,攻击者无利可获,攻击效能为0;若0<ε(ei→j)<1,说明攻击代价小于攻击收益,攻击者有利可获,攻击效能为1-ε(ei→j);若ε(ei→j)=0,说明攻击代价为0,攻击效能为1.
4.5 原子攻击成功概率计算方法
原子攻击成功概率表示攻击者实施攻击,成功攻陷目标节点的可能性.在漏洞利用成功概率相同时,攻击者往往倾向于对攻击代价小,攻击收益高也即攻击效能高的漏洞发动攻击,故攻击效能与原子攻击成功概率正相关.
假设BSNAG中的资源状态节点si转移到状态节点sj,需要攻击者对网络中某漏洞vj实施攻击ei→j,则原子攻击ei→j成功的概率:
P(ei→j)=P0(vi)×AE(ei→j)
(12)
其中,AE(ei→j)为原子攻击效能;P0(vj)为漏洞vj的利用成功概率.
5 基于BSNAG模型的风险评估
5.1 静态风险评估
静态风险评估可以发现目标网络中存在的潜在危险,帮助网络安全员了解网络状况.贝叶斯攻击图中,一般根据先验概率对节点风险进行静态评估.某节点的先验概率为该节点及其父节点的局部条件概率的联合概率,因此,为了计算节点先验概率,需先计算出节点局部条件概率.
局部条件概率反映某资源状态节点可能会遭受的风险.∀sj∈Sm∪St,sj的局部条件概率与其父节点Pa(sj)到该节点的原子攻击有关,贝叶斯攻击图中父节点间存在两种依赖关系:{And,Or},状态节点sj的局部条件概率的计算公式如下:
1)父节点间依赖关系fj=And时:
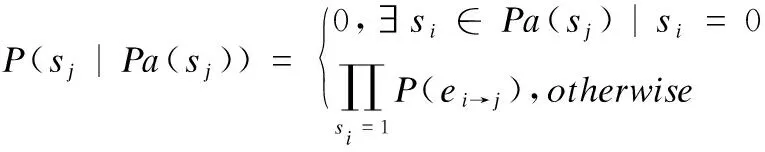
(13)
2)父节点间依赖关系fj=Or时:
(14)
∀sj∈Sm∪St,由局部条件概率公式进一步计算sj的先验概率:
(15)
若∀sj∈Sb,sj的先验概率根据专家经验赋值.
5.2 动态风险评估
网络中攻击事件的发生、漏洞补丁的更新、安全条件的改变都会影响资源状态节点的概率,为了能动态评估网络风险,需要计算状态节点的后验概率,多数研究学者在风险评估时一般根据贝叶斯推理计算节点后验概率.但随着资源状态节点的增加,利用贝叶斯推理计算后验概率时,时间复杂度可能会以指数级的速度增长,不能及时地评估网络状况.
团树传播算法在计算后验概率时,能降低时间复杂度.团树传播算法的首要步骤是将贝叶斯攻击图转换为团树,转换过程由构造端正图、三角化以及构造团树三部分组成,其中,贝叶斯攻击图对应的端正图三角化,实质是端正图中节点的消元过程,也是生成团树的过程[19].端正图转换为团树比较常用的两种消元算法是最小缺边搜索算法和最大势搜索算法,最小缺边搜索算法的消元顺序通常优于最大势搜索算法的消元顺序[20],而消元顺序的优劣与消元成本有关,对于消元成本的量化详见文献[21].本文从消元成本的角度出发,提出了新的消元算法:删除节点次序算法.
5.2.1 删除节点次序算法
贝叶斯攻击图及其对应的端正图中,节点间的连接构成了边.边的数量越少,说明节点间的连接越少,图对应的复杂度越小,在进行概率推理时计算复杂度也越小,相应的消元成本也越小.因此本文根据图的复杂度大小提出了删除节点次序算法,其中图的复杂度用边的数量衡量,具体步骤如下:
(a)删除端正图中的节点时,也会删除与该节点有关的边,删除的边数量越多,剩余端正图的边数就越少,对应的复杂度就会越低.用DE表示删除边的数量,与端正图的复杂度成负相关.
(b)删除端正图中的节点后,为了使该节点的全部邻节点在一个团中,可能会在邻节点间增加部分边.剩余端正图的边数会增加,对应的复杂度也会增加.用AE表示增加的边数,与端正图的复杂度成正相关.
(c)由(a)、(b)分析可知,删除的边数DE和增加的边数AE,会影响剩余端正图的复杂度IC,因此复杂度可以用IC=AE/DE量化.本文根据删除节点后,剩余端正图的复杂度大小,确定端正图中的节点删除次序.删除某节点时,其对应的剩余端正图的复杂度,相比于其它节点对应的剩余端正图的复杂度较小时,优先删除此节点.以此类推,从而确定删除节点的次序.
综合上述分析,本文提出了删除节点次序算法DNO_Alg,DNO_Alg算法的具体步骤如下:
输入:贝叶斯攻击图BSNAG对应的端正图
输出:节点删除次序
1.初始化队列Q,用来存储节点删除次序
2.判断节点数目是否大于3,若是,执行步骤3;否则,执行步骤5
3.计算出每个节点对应的复杂度IC=AE/DE
4.找出最小复杂度IC对应的节点,并将该节点存入队列Q且从图中删除该节点,节点数递减,执行步骤2
5.输出节点删除次序队列Q,算法终止
DNO_Alg算法和最小缺边搜索算法的共同之处:在计算某节点删除、增加的边数时,都需要对该节点的全部邻节点进行搜索.故DNO_Alg算法和最小缺边搜索算法的时间复杂度相似.
5.2.2 团树传播算法
在用本文提出的DNO_Alg算法确定节点删除次序后,借鉴文献[19]中的转换过程,得到BSNAG模型对应的团树Tb,然后使用团树传播算法计算后验概率.团树传播算法的具体步骤:
输入:贝叶斯攻击图BSNAG以及对应的团树Tb,检测到的攻击证据集合O
输出:每个状态节点的后验概率
1.利用BSNAG初始化Tb,即将与状态节点有关的原
子攻击成功概率以及先验概率存入Tb,由此得到各个团的的概率分布;
2.在团树Tb中,将攻击证据对应的状态节点后验风险概率设为1;
3.找出攻击证据对应的状态节点所在的一个团Tp,将该团作为枢纽进行概率推理;
//信息收集与分发
4.for(与Tp相邻的团Tc)
5.调用信息收集函数CollectMessage(Tp,Tc);
6.调用信息分发函数DistributeMessage(Tp,Tc),并将分发的信息存储在团Tc对应的信息存储函数中;
7.endfor(4)
//计算BSNAG中状态节点的后验概率
8. for(BSNAG中每一个非证据变量si)
9.找出一个含有si的团Ts;
10.将初始化的概率分布和信息存储函数相结合,得到攻击证据下的团Ts的概率分布h(Ts);
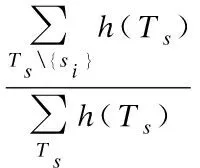
12.returnPpos(si);
13.endfor(8)
6 仿真实验
6.1 仿真网络环境
为了验证该评估模型的可行性,搭建了一个小型仿真网络环境,其网络拓扑结构如图1所示.
图1中防火墙1将网络划分成两部分:外部网络、内部网络,其中,内部网络由DMZ,子网1,子网2三部分组成.防火墙1的安全策略:不能直接访问子网1,子网2,但允许攻击者访问DMZ区域中主机H0上的web服务和H1上的ftp服务.DMZ、子网1、子网2之间的通信规则:DMZ中的H0可以访问H2;H1可以访问子网1中的H3和子网2中的Mail服务器; H2、H3可以访问子网1中的H4,H4可以访问子网2中的数据库服务器和Mail服务器.子网2中的服务器设备之间不能相互访问.
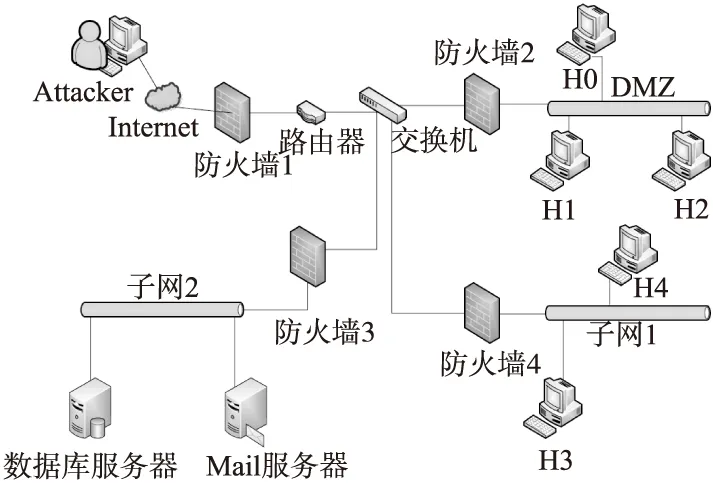
图1 网络拓扑结构图Fig.1 Network topology diagram
本文对网络不同区域中的主机使用Nessus进行漏洞节点扫描,对检测到的漏洞节点信息进行汇总,如表6所示.
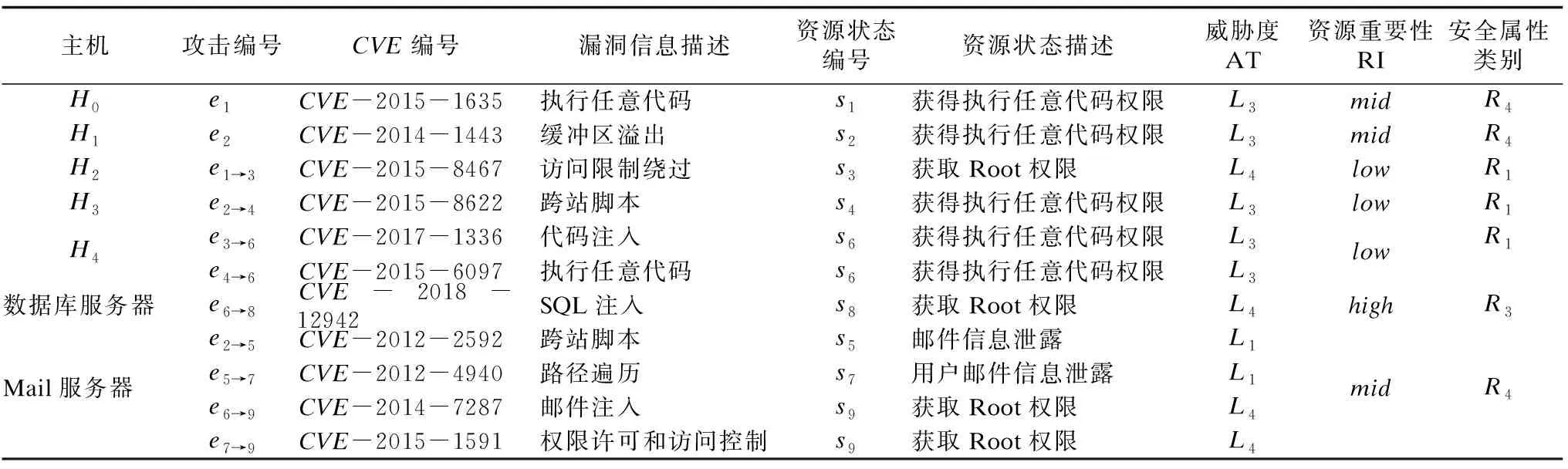
表6 漏洞信息表Table 6 Vulnerability information table
根据实验网络的拓扑结构、漏洞节点情况,得到贝叶斯攻击图BSNAG,并利用DAO_Alg算法确定消元顺序,由此将BSNAG模型转换为相应的团树,BSNAG模型及其对应的团树,如图2所示.
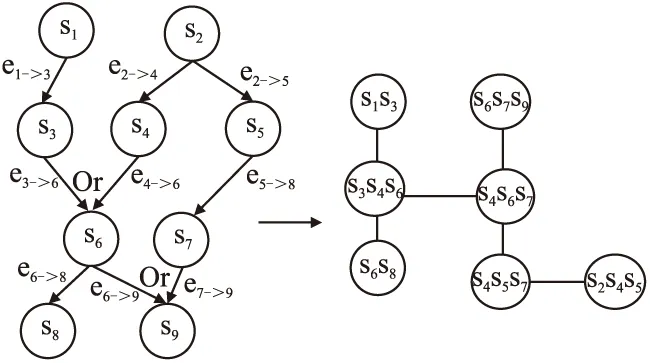
图2 BSNAG模型及其对应的团树Fig.2 BSNAG model and group tree
其中,DAO_Alg算法确定的消元顺序,如表7所示.
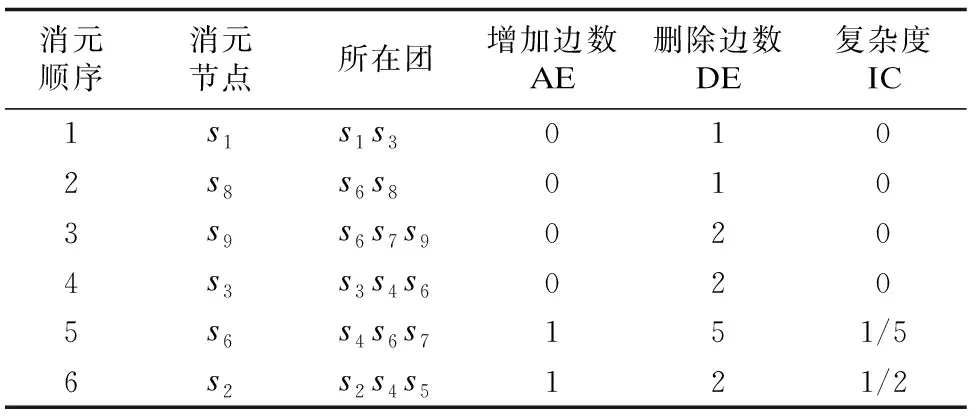
表7 消元顺序表Table 7 Elimination sequence table
6.2 实验结果及分析
使用第4节和5.1节中的量化公式,并结合专家经验对原子操作成本及其权重分别赋值0.3、0.2,计算图2中考虑攻击效能的节点先验概率Ppre,同时计算出不考虑攻击效能的先验概率P1;利用入侵检测系统snort检测到节点s7对应的原子攻击e5→7,使用5.2节中的团树传播算法计算节点后验概率Ppos,计算结果如表8所示.
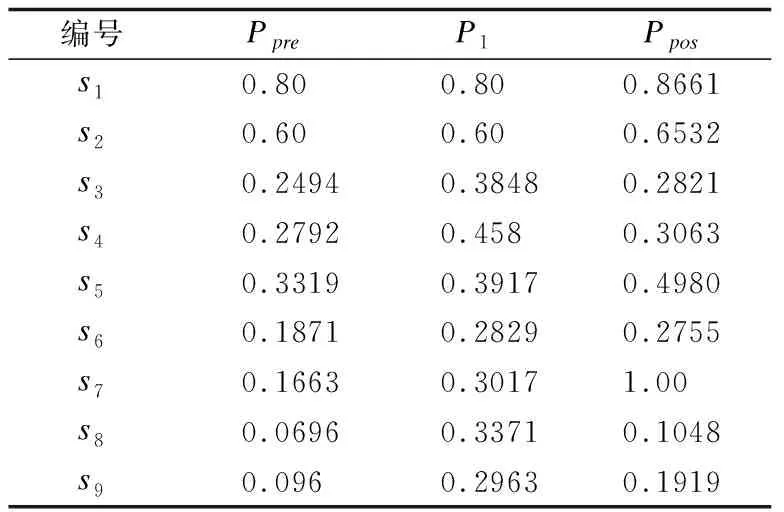
表8 节点概率表Table 8 Node probability table
根据表8,绘制考虑攻击效能的先验概率和不考虑攻击效能的先验概率对比图,如图3所示.
对图3中的先验概率分别从纵向和横向两个角度进行分析:
①从纵向角度可知:相同的节点在考虑攻击效能时的概率小于或等于不考虑攻击效能的节点概率.根据本文第4节可知,攻击效能和漏洞利用成功概率的乘积为节点对应的原子攻击成功概率,因为攻击效能的取值为0~1,所以考虑攻击效能后,节点对应的原子攻击成功概率小于或等于节点对应的漏洞利用成功率;对于未考虑攻击效能的节点,节点对应的原子攻击成功概率直接为漏洞利用成功率,大于或等于考虑攻击效能的原子攻击成功概率.而先验概率是基于原子攻击成功概率求得的,故本文考虑攻击效能的先验概率小于或等于不考虑攻击效能的先验概率.引入攻击效能的前提是假设攻击者是趋利的、理性的,在考虑攻击效能后,节点对应的风险值减少,表明攻击者在对网络发动攻击时会根据攻击效能的取值,有选择地对节点发动攻击.
②从横向角度可知:节点间先验概率的相对大小会因为引入的攻击效能发生改变.从图3中可以看出,与不考虑攻击效能相比,考虑攻击效能后,相邻节点s4和s5,节点s6和s7,节点s8和s9的先验概率的相对大小发生了改变.这是因为攻击效能由攻击代价和攻击收益共同决定,攻击者会根据付出的代价和获取的收益有选择地攻击节点.
利用文献[9]中的最大概率攻击路径选择算法得到没有引入攻击效能时,攻击者攻击目标节点s8、s9时最可能选择的路径分别为{s2,s4,s6,s8}、{s2,s4,s6,s9};而引入攻击效能后,攻击者攻击目标节点s8、s9时最可能选择的路径分别为{s2,s4,s6,s8}、{s2,s5,s7,s9}.经过对比分析:加入攻击效能后,攻击者对目标节点s9的评估结果发生了变化,更符合攻击者在实际情况下会选择的攻击路径.
从表8中还可以得到:在检测到攻击证据o5→7后,所有节点的后验概率Ppos均大于其对应的先验概率Ppre.节点s7及其对应的父节点s5,子节点s9,兄弟节点s6的后验概率Ppos增加幅度分别为0.8337、0.1063、0.0959、0.0884,概率变化较大,说明节点风险值受攻击事件的影响较大;表中其它节点的后验概率Ppos增加幅度均小于0.07,概率变化较小,说明节点风险值受攻击事件的影响较小.因此,当检测到攻击证据o5→7后,选择对受影响较大的节点给予防护,即对节点s5,s6,s7,s9给予保护措施来降低节点风险.
从上述分析可知,静态和动态评估相结合,可以实时根据网络情况有针对性的防护网络中的节点.
为了验证团树传播算法在计算节点后验概率的时间复杂度优于贝叶斯推理,本文增加节点数,进行了多次试验,时间复杂度对比如图4所示.
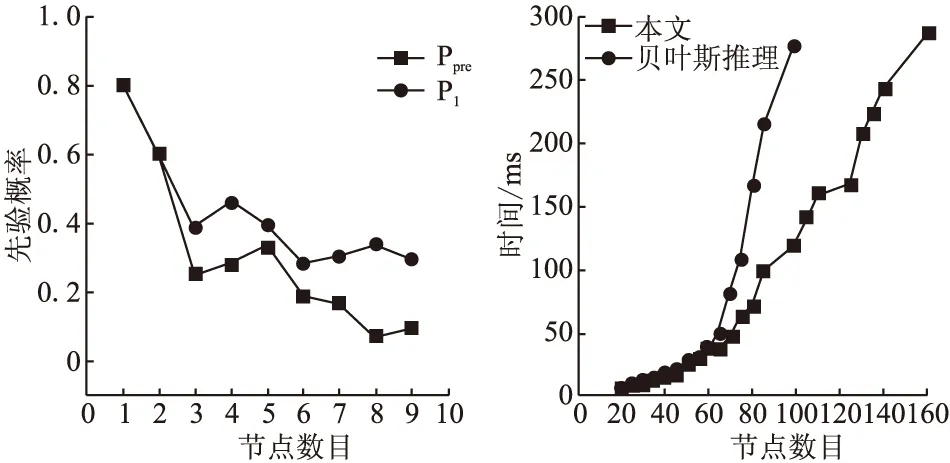
由图4可知,当网络中的节点增多时,相比于使用贝叶斯推理计算后验概率时,使用团树传播算法能降低时间复杂度.
同时为了验证本文提出的DNO_Alg算法的消元效果,和最小缺边搜索算法在消元成本方面做了对比分析.本文在做实验时,利用指定的节点数N和边数E构造随机图,并用构造的随机图表示端正图,其中,随机图的构造过程为:1.确定节点数N和边数E;2.随机生成两个不同的且在0~N之间的数g,h;3.用线把g,h对应的节点连接起来,由此生成随机图的一条无向边;4.重复步骤2-3直到构造的随机图中有E条边.在实验时,通过对节点数N和边数E进行设置,构造不同规模的随机图.
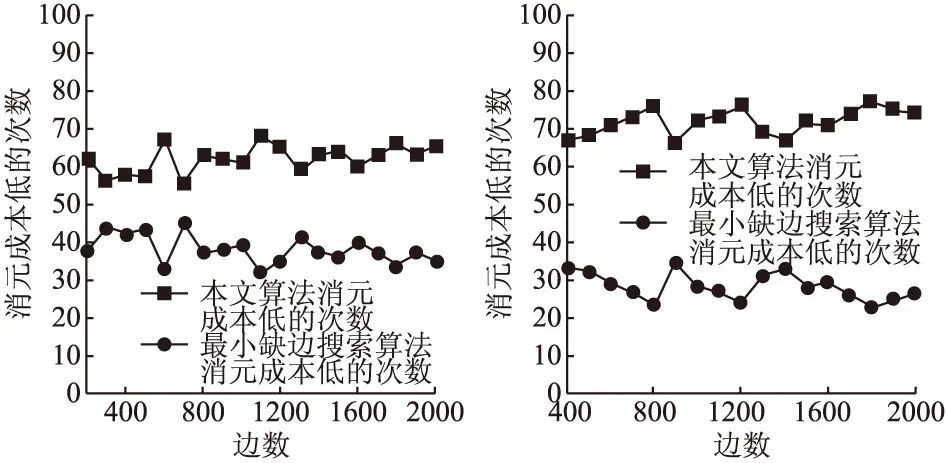
为了验证DNO_Alg算法的可行性,本文指定节点数N=100和边数E=200,构造了100个不同的随机图.然后在这100个随机图上执行最小缺边搜索算法和DNO_Alg算法,比较100个随机图中最小缺边搜索算法和DNO_Alg算法对应的消元成本低的次数.改变边数E的取值为300,400,…,2000,重复上述步骤,实验结果如图5所示.改变节点数N=200,边数E分别取400,500,…,2000,实验结果如图6所示.
从图5,图6可以看出,DNO_Alg算法在降低消元成本方面相比于最小缺边算法有一定的优势,随着节点数的增多时,DNO_Alg算法的优势更加明显,更适应于大规模网络.
7 结束语
网络安全风险评估一直是国内外比较关注的热点,本文对网络安全进行风险评估时,在前人的基础上,提出了一种新型贝叶斯模型的网络风险评估方法.首先,依据当前的网络攻击者是理智的,将由原子攻击代价和原子攻击收益量化的攻击效能和漏洞利用成功概率相融合,计算原子攻击成功概率,进一步计算节点先验风险概率对网络进行静态评估;其次,提出节点删除次序算法NDO_Alg,将贝叶斯模型转换为团树.最后,利用团树传播算法计算后验风险概率对网络进行动态评估.实验结果验证了本文所提模型不仅能提高网络风险评估结果的准确性,还能降低计算后验风险概率的时间复杂度.后续研究重心将进一步考虑防御措施对评估的影响以及再进一步降低计算后验概率的时间复杂度.

