T型小通道气液两相流动特性的数值研究

雷 丽，黄楠燕

(山东大学 能源与动力工程学院，山东 济南 250061)

气液两相流及其流动特性对化学、石油等工业有着重要的影响。这是一种复杂的现象，它将单相流体流动(粘性力、惯性力和压力)与两相流(界面力、接触角、传热传质和动量等)的特性结合在一起。两相流的产生可以归因于不同相的变化或混合。因此，研究不同工况下小通道内气液两相流动很有必要。然而，气液两相流动与单相流动相比很复杂，因此，为了更好地理解气液两相流动，人们进行了大量的研究[1-3]。

在常规管道中，实验比较常见的流型有：泡状流、弹状流、层流、环状流和雾状流[4-7]。Weisman等[7]研究了内径为11.5 mm至127 mm的水平圆管的两相流动。结果表明，管径和流体性质(表面张力、粘度和密度)对流型转变的影响在该管径范围内不显著。然而，随着管径的减小，重力的影响逐渐减小，在小通道中，表面张力起主导作用。正如Coleman和Garimella[8]所述，管径对流动状态转变有显著影响。Triplett[9]等人在直径为1.09～1.45 mm的圆形和三角形微通道中进行了实验研究，证实了这一结论。他们发现现有的常规通道的相关模型与小通道的实验数据吻合较差。Deendarlianto[10]等人利用VOF方法对26 mm水平管内塞状流流动进行了CFD模拟研究。数值模拟的流型和含气率与实验结果吻合良好。利用矢量云图观测了气塞内部的流动循环。Parvareh等人[11]比较了VOF方法计算的数值气液界面与采用电阻层析重建的实验结果。数值计算结果与实验结果在水平和垂直管道上吻合较好。López[12]等人利用高速摄像法和数值模拟对14 mm直径水平管道内的气液两相流动进行了综合研究。数值计算结果与实验结果吻合较好。

国内外学者对常规通道进行了大量研究，对小通道的研究相对较少。并且，与实验方法相比，数值方法能以更低的代价获得更详细的两相流流动特性。因此采用数值模拟方法研究小通道气液两相流具有重要意义。本文建立了三维T型小通道的物理模型，并利用CFD方法对其进行数值模拟，以获得管内的气液两相流动特性参数。通过与实验流型的对比验证了该模拟的可靠性，并对该通道所观测到的泡状流、弹状流和环状流的流型、压力和压降以及间歇流的气泡生成和气泡长度进行了数值分析。

1 T型通道的模型化

1.1 控制方程

采用VOF方法对水平小通道内的两相流动进行了数值模拟。该模型可以追踪自由边界，气液相的相互作用是由表面张力驱动的。在该模型中，两相体积分数之和为1。在VOF模型中，如果网格单元中全是气相，则该单元网格中气相的体积分数为1，如果充满了液相，则体积分数为0，多相流体网格单元中体积分数介于0和1之间。

此外，VOF模型还同时使用了不可压缩的Navier-Stokes方程。在计算中，输运守恒和动量的控制方程在计算域内连续求解。VOF方法中的控制方程有以下三个：

连续性方程：

(1)

动量方程：

(2)

体积分数方程：

(3)

利用体积分数加权平均法得到了上述方程的参数。关于计算方法的具体信息可以在小通道两相流的相关研究中找到[13-14]。

1.2 物理模型及网格划分

计算域的几何形状、边界条件和计算网格的截面如图1所示。该T型管的内径为5.16 mm。由图1(a)可知，气液两相入口设置为速度入口，流体出口设置为压力出口。空气为主相，水为次相，采用无滑移壁面对管壁进行建模。空气和水的物理性质参数如表1所示。

表1 流体的物理性质参数

计算域采用结构化网格进行划分。为了正确求解边界层，对壁面附近进行加密，如图1(b)所示。为了进行网格独立性验证，采用341,263 ～ 1,020,564不同网格数对几何图形进行网格划分，发现这些网格数对流型的发展影响很小，但是对气液界面的影响很大。综合考虑，选择网格数为800,040进行数值模拟。

(a)计算域，(b)几何截面的正交网格图1 计算模型

1.3 数值求解方法

仿真采用了基于压力的求解方法，利用非迭代分布法计算连续性方程、动量方程、和体积分数方程的时间步长，利用一阶逆风格式对动量方程和能量方程进行离散化，采用分段线性界面方程来计算体积分数方程。每次计算的时间步长采用变时间步长来确定，并且库朗数为0.25。由于流动的不稳定性，计算模型选择瞬态模型。

2 结果与讨论

2.1 模拟的流型与实验结果的对比

为了验证模拟水平管内气液两相流流态的真实性，对选定的实验工况进行了模拟。在实验和模拟过程中，我们发现了三种流型：泡状流、弹状流和环状流。高速摄像机拍摄的照片和CFD模拟结果的对比图如图2所示。泡状流、弹状流和环状流的气速分别为0.12、0.12、3.42 m/s。对应的水的表观速度分别为0.588、0.17和0.92 m/s。因此，泡状流、弹状流和环状流的气液流速比分别为0.204、0.706和3.717。气液流速比对流型的转变有很大影响，不同流型有不同范围的气液流速比。

如图2所示，实验所捕捉的照片与模拟的相云图吻合较好。其中，相云图用红色来表示气体体积分数，蓝色表示液体体积分数。这三种流型的不同是由于气液流速比的变化而产生的。泡状流的气相是分散的，液相是连续的。此外，由于重力的作用，气泡在管道上部流动。随着气液流速比的增大，气泡所受到的剪切力增大，气泡的形成时间变长，气泡长度变长，形成弹状流。在该流态下，空气为离散相，水为连续相，如图2(b)所示。这两种流型以受到表面张力为主导。环状流的气相和液相是连续的。空气从管中流过，将液体推向管壁形成液膜。环状流的气液流速比最大，因此受到惯性力为主。

图2 实验流型与数值模拟结果的比较

上述实验流型与模拟流型的比较结果显示，模拟的泡状流、弹状流和环状流流型与实验结果吻合，说明本文所用的CFD方法可较为准确地反映水平小通道气液两相流的实际流动情况。

2.2 间歇流气泡的形成过程

如图3所示，以弹状流为例，研究T 型小通道间歇流气泡的形成过程。初始时刻，通道中全部是水，空气从入口处开始进入通道。随着时间的推移，空气到达T型管混合区，由图3(a)可知，只有部分通道被气泡占据。随着液相和气相的持续流动，气泡逐渐变大变长并且向下游流动，气泡尾部变薄，如图3(b)所示。最后气泡尾部被剪断，形成弹状流气泡，如图3(c)所示。T型小通道气泡的形成是气液两相在惯性力、重力和剪切力作用下克服表面张力的结果。

图3 小通道内弹状流气泡的形成过程

为了进一步研究气液流速对两相流流型的影响，保持气相流速为0.12 m/s不变，逐渐增加液相流速进行模拟。液速的变化范围是0.17～0.588 m/s，一共模拟了5种工况。由图4可知，气相流速不变，随着液相流速的增加，气泡长度逐渐减小。这是因为气相流速一定，液相流速越大，气泡受到的剪切力越大，气泡形成的时间变短，因此气泡长度变小。

图4 气泡长度随液相速度的变化

2.3 流体的压力分布

图5展示了水平小通道内气液两相流泡状流、弹状流和环状流三种流型的压力云图。如图5(a)和(b)所示，充分发展的气泡沿管道从左向右流动，由于表面张力的影响，气液两相界面出现明显的压降，气泡内部压力远大于周围液相压力。同时，气弹的压力大于相邻的液弹的压力，并且沿着流动方向，气弹和液弹压力都逐渐减小。另外，由于泡状流和弹状流的表面张力大小一样，但是泡状流受到的剪切力更大，因此泡状流气泡内的压力大于弹状流气泡内的压力。

图5 泡状流、弹状流和环状流的压力云图

对于环状流来说，由于上下壁面液膜厚度较小，垂直方向的压力分布没有明显的变化；由于沿程损失的影响，水平方向的压力值逐渐递减。此外，环状流的气液界面有较大波动时，会形成很大的压降。如图5(c)所示，气芯也经常与液滴混合，液滴是通过撕裂管壁的液膜而形成的，因此液滴内部压力与周围流体压力相比较大。

2.4 流体的压降分析

在一般的压降分析中，压降分为摩擦压降、重力压降和加速度压降。在水平小通道的空气-水两相流动中，不存在重力压降。研究发现，由加速度引起的压降的贡献通常小于当前工作中总压降的2%。图6展示了气液两相流典型工况的泡状流、弹状流和环状流三种流型的模拟压降结果，与图2工况一致。

从图6(a)和(b)可以看出，泡状流和弹状流的压降分布是周期性波动的。压降信号有高有低，这取决于通过截面的是气泡还是液弹。此外，由于弹状流的气液流速比大于泡状流，弹状流气弹的长度更大，因此弹状流的压降曲线相比于泡状流具有更小的振动频率。由于泡状流受到更大的剪切力影响，泡状流的压降曲线有更大的峰值和低值。

从图6(c)可以看出，环状流的压降与间歇流相比变化更不规则。气液两相的流量对气液两相的分布有很大影响，与间歇流相比，环状流具有较大的气液流速比，气液两相间波动剧烈。因此，环状流的压降更加无序，在50～200 Pa范围内变化较大。

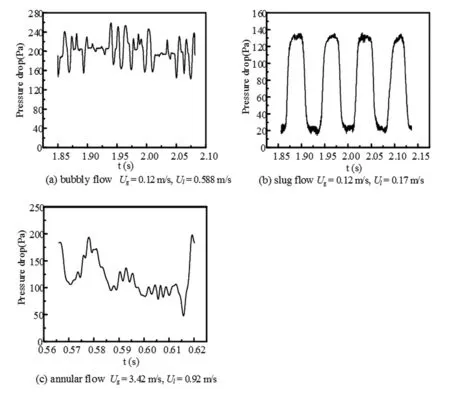
图6 泡状流、弹状流和环状流压降随时间的变化

3 结论

本文对水平T型小通道进行了数值模拟，通过与实验流型的对比，验证了该模拟的可靠性，并对该通道所观测到的泡状流、弹状流和环状流的流型、压力和压降以及间歇流的气泡生成和气泡长度进行了数值分析，结论如下：

(1)气液流速比是影响流型的一个重要因素。不同的气液流速比会得到不同流型，环状流的气液流速比最大，因此受到惯性力为主。气相速度一定，液体速度增大时，气泡长度变小。T型小通道气泡的形成是气液两相在惯性力、重力和剪切力作用下克服表面张力的结果。

(2)间歇流以表面张力为主导，因此其气泡内的压力远高于周围液相的压力。环状流垂直方向压力分布没有明显变化，水平方向的压力沿着流动方向逐渐减小。间歇流中气相是离散相，液相是连续相，因此其压降随时间的变化呈周期性分布。峰值的变化取决于通过截面的是气弹还是液弹。环状流的气液界面波动相比于间歇流没有明显规律，当气液界面波动较大时，压降增大。