纯归纳逻辑及其存在问题探析

董英东

（湘潭大学碧泉书院，湖南 湘潭 411105）

1 语境和记法

纯归纳逻辑所使用的语言为一阶逻辑语言（L），包括关系符号R1，R2，...Rq，参数r1，r2，...... ，rq，常元an，其中n∈N+={1,2,3，......}，以及既非函数符号也非等值符号等辅助符号。ai指在某些集合中的所有不同个体的名称。令SL表示该语言L的一阶句子集，QFSL表示该语言中的句子的自由量词。令T表示L的结构集的域{a1，a2，a3，...}，且ai的解释为ai本身。

为了刻画纯归纳逻辑想要解决的基础问题，假设某个主体属于某种结构，可表示为M∈T，此时很难确定M中的哪些主体是真的。这样将面临的问题是：

Q：在这种零知识、逻辑的或理性的情况下，什么样的信念才能使我们的主体能够确定句子θ∈SL且在M中是真的？

这个问题中涉及几个术语。首先“零知识”意味着主体并不希望对ai和Rj做出解释。在这些情况下，所能假定的就是公理，且不可能带来新的事实，因为它们属于某个特定的群体，这样可能会产生混淆。

从某种意义上来说，类似于数学的“纯归纳逻辑”和哲学的“应用归纳逻辑”二者之间是有区别的。对于许多哲学家来说，在后者的语言中希望带有解释，如果没有解释，那就只能是纯数学而不是哲学。这就是为什么蓝绿悖论是哲学中的一个悖论，在数学中只是一个无效的论证的原因。尽管如此，无论是否是数学家，需要确保在进行解释的时候以免陷入潜意识的解读。卡尔纳普本人非常了解这种分歧，而且知道忽视它会带来问题，并且试图去解释它。事实上，在他的论文中，他将“归纳逻辑”描述为对这种零知识主体的研究，并称之为“主体”。[1]

第二个无法解释的术语是“逻辑的”和“理性的”。在这种情况下，我们不提供任何关于逻辑的和理性的定义，并将其看作是直观的。因为我们主要为了提出和数学家所研究的相似的合乎逻辑理论的规则。这种情况与递归理论中“有效性”的直觉概念相似。

第三个无法解释的术语是“信念”。在纯归纳逻辑中，我们用（主观的）概率来确定信念，或更准确说为信念度。荷兰赌论证为这种信念提供了强有力的论证，主要采用“概率”或者“概率函数”来表达我们所说的思想：

2 概率函数

函数w：SL→[0，1]为基于SL的概率函数，如果对所有的θ，φ，∃xψ(x) ∈SL，

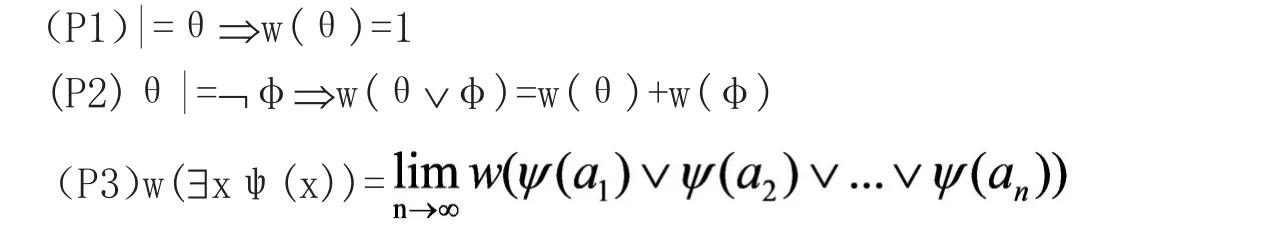
条件（P3）指盖夫曼条件[2]，并且在该语境中相对于传统条件（P1）和（P2）为特殊条件。其常用于刻画域中的a1,a2,a3,…。

所有标准的、简单的和所有期望的概率函数的性质都来自（P1-3）：

命题1 令w为基于SL的概率函数[3]。那么对于θ，φ∈SL，

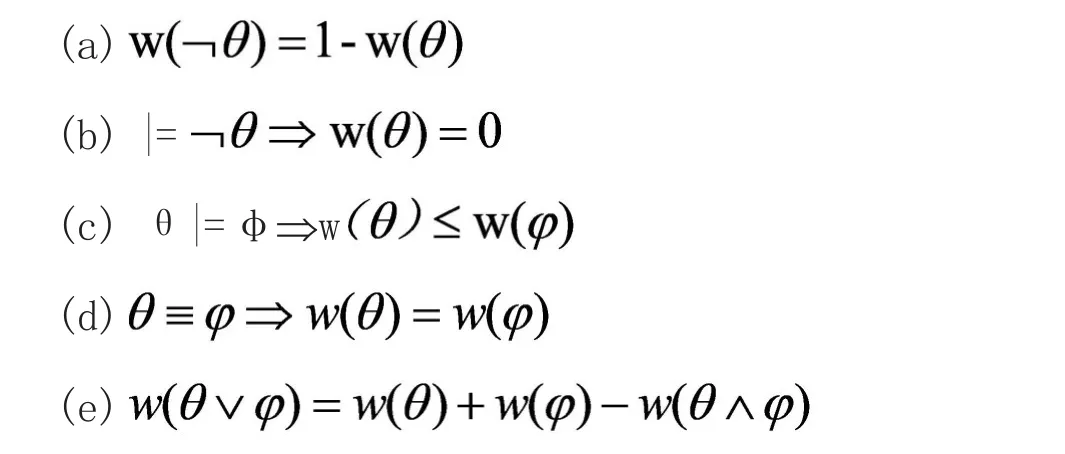
由于SL中语句的多样性，使得概率函数变得异常复杂。首先我们给出盖夫曼定理：

定理2 假设w:QFSL→[0，1]且满足（P1）和（P2），对于θ，φ∈QFSL，对任意的θ，φ，∃xψ(x)∈SL，w存在一个基于SL的概率函数的一元的外延满足（P1）、（P2）、（P3）。

在该定理中，用“博弈”表示理性的概率函数作为对自由语句的量化，可以简化为：

3 状态描述

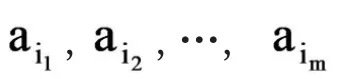
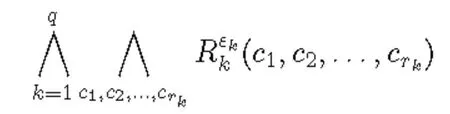
也可以用大写的字母Θ，Φ，Ψ等表示状态描述。通过利用定理2以及不相交典范公式定理可以直接得出:

定理3 一个概率函数是由基于其上的状态描述的值确定的。

事实上，博弈主要起得到了状态描述的作用。回顾问题Q，现在可以将其归结为：

Q：在零知识、逻辑或者理性的情况下，概率函数w：SL→[0,1]应该是主体接受，w(θ)相对于主体的概率，语句θ∈SL在外部结构M中是真的。

那么主体应该如何做出这个选择呢？就纯归纳逻辑而言，可通过应用：

4 理性规则

也就是说，主体制定合理的或逻辑的原则或概率分配规则，然后采用符合这些原则的概率函数。

但是就纯归纳逻辑而言，事实上并非如此。正如已经提到过的，理性行为意味着什么，或者更为特别的是可以认识到非理性的行为，对于纯归纳逻辑来说，试图把这些感觉作为形式原则来刻画，然后继续去研究它们的后承和与其它假定合理的原则的关系。因此，纯归纳逻辑是一个实验，利用它可以自由地研究任何原则，只要其与形式有某种相关性，也就是说可以不必考虑理性的某些刻画。为此，不需要知道理性是什么，就像那些试图提出“有效性”的数学家在开始之前并不需要知道他们研究的是什么一样。而且“理性的”概念可能会从这些研究中概括出来。

在某种程度上，这与“集合论”中的情况类似，根据“集合的世界”的一些直觉提出公理，其中一些公理几乎被普遍接受，而另外一些则是高度争议的公理，然后研究它们的后承。有时这些公理可能是不一致的，但感觉上则是通过这种有选择的研究，我们正在接近理解甚至接近集合理论的真理。所以纯归纳逻辑也是如此，甚至可能会与直觉相冲突。

就这样的“理性原则”而言，到目前为止，它们似乎有三个主要来源：对称性、相关性和不相关性。在基于对称性的原则中，所采用的概率函数w应该保持对称性。从这样一个被广泛接受的知识开始，以后将在不经过进一步的明确提及的情况下假设它们是真的。

常元可交换原则，Ex

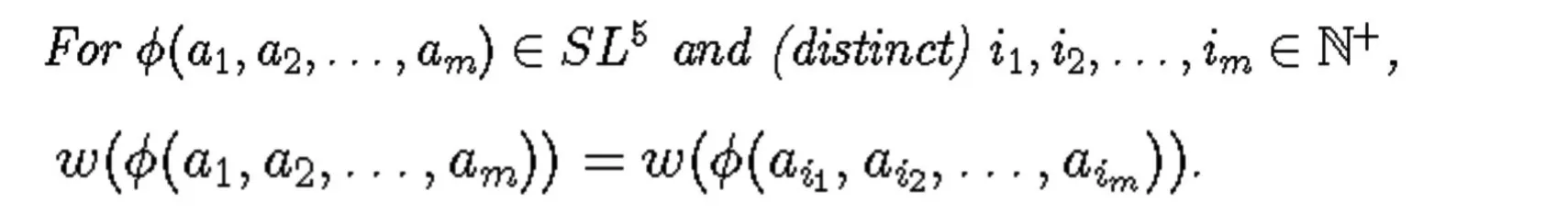
这里的合理推理是指主体对于任何一个ai都不了解，所以在分配概率时对他们进行不同的处理是不合理的。

以完全相似的方式，可以证明谓词可交换性原则和强否定性原则，并用否定的公式替换关系符号。

现在已经介绍了恒定可交换原则Ex，从w满足Ex的假设出发研究它究竟是什么。纯归纳逻辑之后的一个主要步骤就是通过证明它们必须看起来像某些“简单构件块函数”的组合来证明概率函数满足该原理的表示定理。对于满足Ex的概率函数存在这样的后承，第一个概率函数就是所谓的菲内蒂表示定理。

5 一元归纳逻辑

在约翰逊和卡尔纳普的早期研究中，归纳逻辑的语言被认为是一元的。也就是说，在这里采用的语言L的关系符号R1，R2，...，Rq都是一元的，所以在哲学中常被称为“谓词”符号。假定L是上面的一元语言。

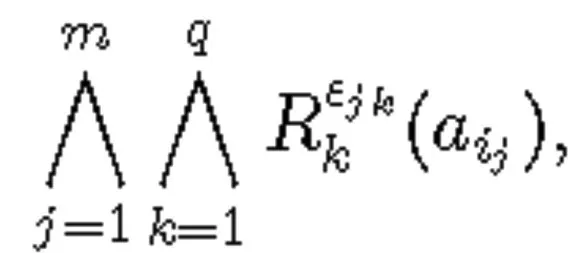
等价的形式为

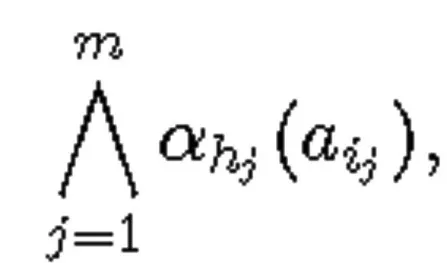
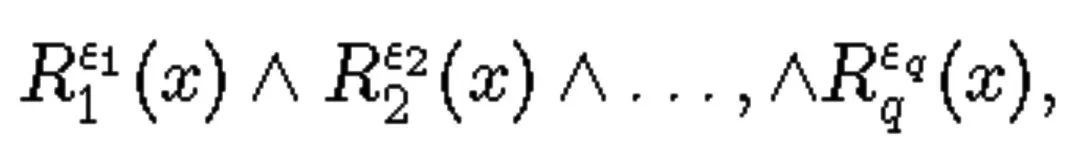
其中ε1,ε2,…,εq∈{0,1}。

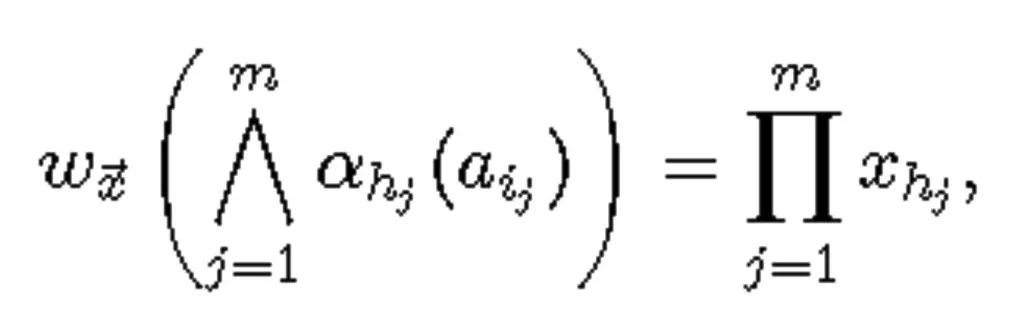
等价于

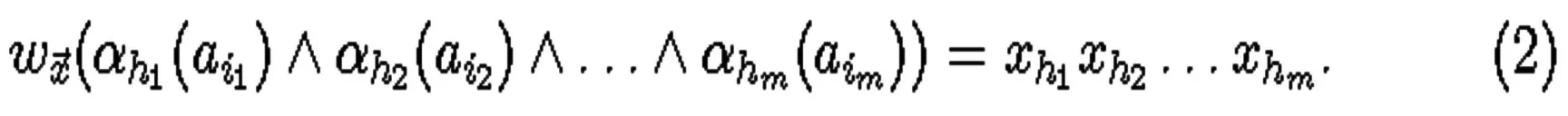
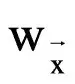
菲内蒂的表示定理

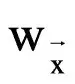
更严格地，仅当

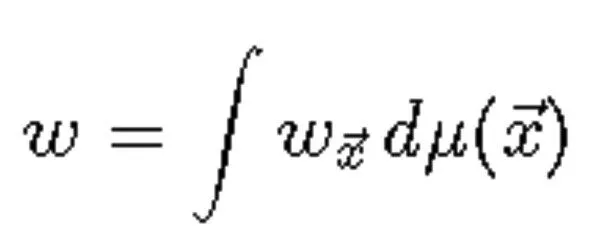
其中μ为基于布尔子集的可数可加的测度：

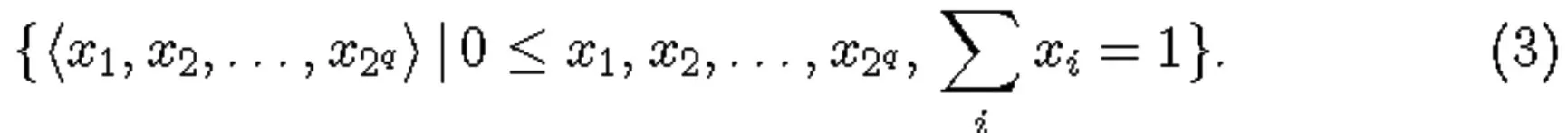
表面上看，这个定理似乎只是数学家的兴趣所在，没有太多关于哲学家会感兴趣的归纳或合理性。然而，它产生的后果和思想在这方面肯定是有利的。这个定理的数学刻画能力在于，它经常使我们能够把关于（3）左边的一般概率函数w的问题转化成关于右边非常简单的概率函数的问题。

定理5 Ex可推出：

实例相关原则（PIR）

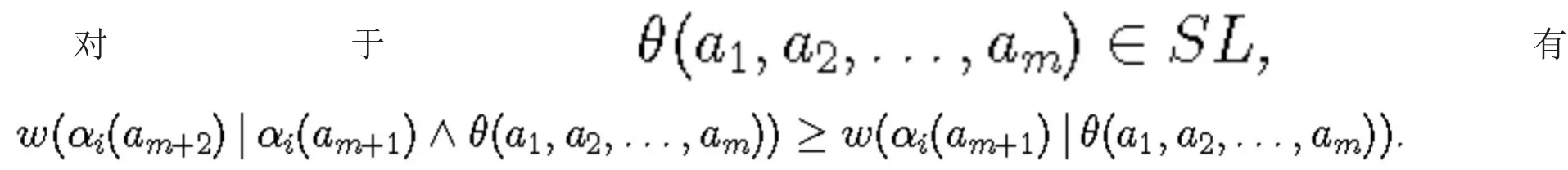
从一个哲学家的视角看，虽然人们可以根据休谟的说法[5]，认为Ex实际上是对自然一致性的假设，在这个意义上可以等同于归纳，这个论证所表明的是，如果你认为Ex是理性的，那么你应该认为PIR是合理的。当然，这个结果可以被看作是对卡尔纳普计划的一个好的处理方法。

常元不相关性原则，CIP

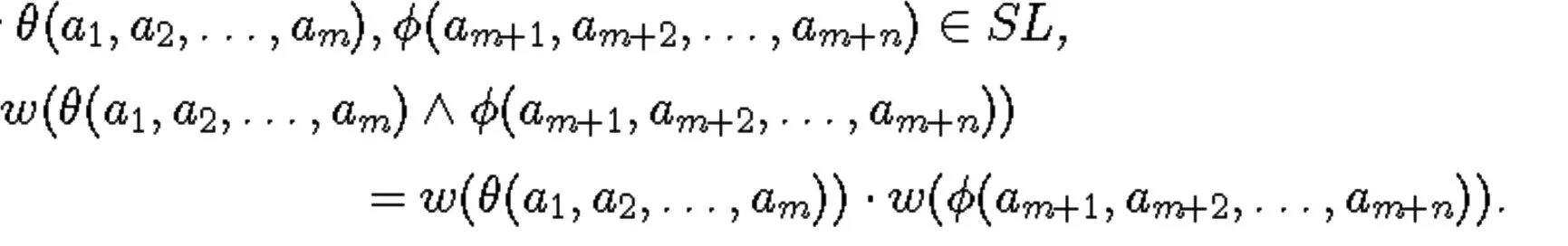
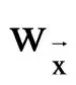
那么我们在这里看到的是由对称原则Ex推出了相关性原则（PIR）和不相关性原则（CIP）。事实证明，这远非一个孤立的现象，而是建议人们可以用对称性的合理性来解释相关性和不相关性原则的感知合理性。

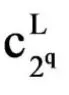
其中mj是原子αj发生的次数

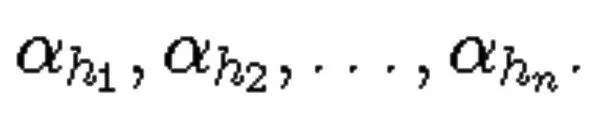
6 多元归纳逻辑

卡尔纳普和凯米尼都提到了这一点[6]。至少有三个原因，首先是简单的、日常的非一元关系归纳的例子是相当稀缺的，但是它们确实存在。

第二个原因是符号和数学的复杂性显著增加，至少与一元的情况相比。关键的原因是对于a1，a2，...，an的状态描述，将不再以一元的方式来处理这些常量。

最后，第三个原因，在形成关于多元关系的信念时，相对缺乏直觉。

下面定义一个状态描述的谱表示这些等价类的多重集的域。

谱可交换性

约翰逊（Johnson）和卡尔纳普（Carnap）在他们的一元语言的情况下采用的原则，称之为：

原子可交换性，Ax

对于状态描述Θ的概率w(Θ)应只取决于Θ的谱。

Ax实际上是一个对称原则。如果我们把原子看作与颜色相对应的话，那么就把这个概率赋予一个状态描述Θ，在置换或颜色的重命名下应该是不变的。总而言之，关于一种颜色的一切是与其他颜色不同的，而不是它是红色还是蓝色或绿色等。

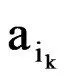
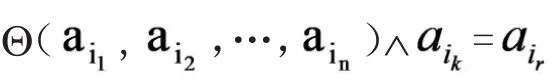
是一致的（带有等价的谓词演算）。

在多元语境中，下面给出一个理性规则：

谱系可交换性，Sx

对于状态描述Θ的概率w(Θ)仅依赖于Θ的谱。如果状态描述Θ，Φ具有相同的谱，那么w(Θ)=w(Φ)。

语言不变性

把纯归纳逻辑扩展到多元语言会产生为什么要修正一个特定语言L的问题。毕竟，我们的主体总是可以想象到的，除了那些语言之外还包含关系符号。此外，主体不希望为这个更大的语言采用概率函数，而这个语言满足了他/她认为合理的原则L的独立性。但是主体的这个愿望能够实现吗？问题是主体可能遵循他/她的合理性原理，并希望（假想的）将L语言扩展为语言L+并且将概率函数w扩充为w+，并且发现表示w+SL的w+对SL的限制是不相同的。换句话说，只要设想使L+中的主体具有理性，就会可能会怀疑w。实际上，从这个角度来看，如果L+完全没有扩展为满足主体偏好的理性原则，那么w可能就不太合理。

为了更具体地假设主体认为Sx（+Ex）是他/她不得不强加给他/她的选择的（唯一）合理的要求。那么主体做出这样的选择可能只是意识到，没有办法将这个概率函数扩展成为一个更大的语言，而仍然希望保持现有的Sx。

Sx的语言不变性，Li+Sx

如果存在一个概率函数族wL，每个语言L上存在一个概率函数w，那么这个簇的每个成员都满足Sx，并且每当语言L1，L2是这样的时候，概率函数w就满足Sx的语言不变性L1，L2，则wL2SL1=wL1。

事实证明，Li+Sx意味着迄今为止提出的理想的多元概率函数的大多数（可能甚至全部）性质。

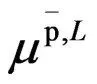
在此的下标0，1，2，3，…表示色组，用0表示黑色，用pi表示所选的颜色i的概率。

（1）根据概率p0，p1，p2，…，选取色组c1，c2，…，cn，使得所选取的c1，c2，…，cn的概率为：

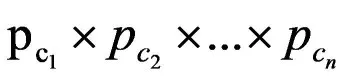
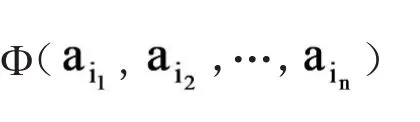
完全性

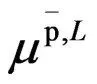
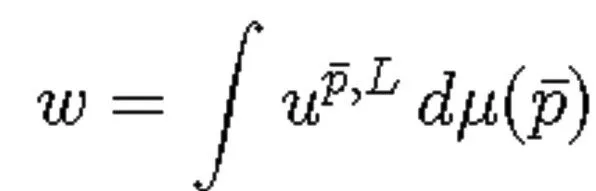
弱不相关性规则，WIP

如果θ，φ∈SL既不是常元，也不是通常的关系符号，那么

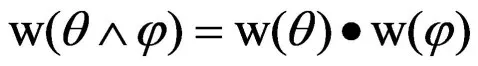
类似地根据定理8，可以证明下面的相关性原则。

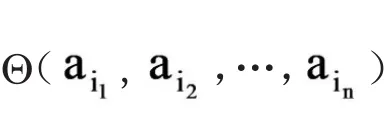
推论11 令w满足Li+Sx。那么根据w，a1和a2是不可区分的，而且其与其它的可以区分的常元ai的概率是0。

7 结论

总而言之，纯归纳逻辑的数学虽然可能揭示一些新原理和原理之间的联系，但总的来说，它是否提供了任何额外的哲学洞察力或理解，甚至对于那些完全理解所涉及的数学的人来说，也是值得怀疑的。

第二个问题是，关于理性原则的三个主要（迄今）的来源，对称性、相关性和不相关性之间的关系。主要讨论了两个对称原理，Ex和Li+Sx。无论这些不相关的原则是否理所当然地作为理性的表达，事实上，对称性似乎是相关原则和不相关原则所产生的基本原则。这可以用相关性来解释，对称性表明未来就像过去，相关性则指出过去发生的事情应该是未来的导向。

在此涉及到了一个与卡尔纳普的思想完全接近的问题。即使主体承认他/她选择的概率函数w应该满足Li+Sx，但这仍然给他/她带来了非常广泛的可供选择的域概率函数。从某种意义上来说，这可能被认为是不幸的，因为它表明两个主体根据这个完全合理的标准，仍然可以指定不同的信念/概率。如果我们能够找到其它的、可接受的理性的原则来削减这个选择时就需要增加“完整性”。

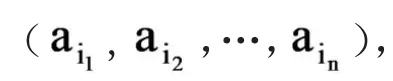
不幸的是，这个概率函数完全没有任何归纳倾向

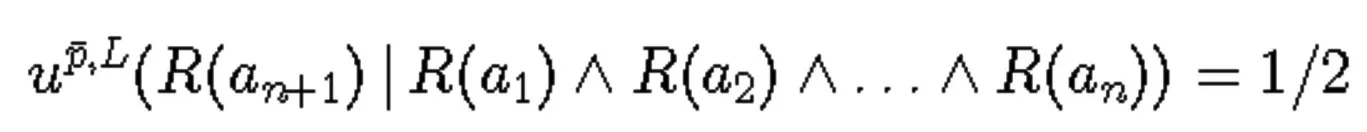
不管n有多大，换句话说，并不需要关注以前的支持性证据R（a1）∧R（a2）∧…∧R（an）给R（an+1）分配一个概率。当n>0时，这个概率函数给出了大于等于0的值，但是究竟n需要多大？显然这是不确定的，这表明可接受的完整性是一个不可能实现的梦想。