双能X射线骨密度仪骨密度测量值线性校正及不确定度评定
/ 上海市计量测试技术研究院
0 引言
随着人口老龄化的日趋严重,作为老年性疾病之一的骨质疏松症及其引起的并发症越来越受到社会关注,因此,对骨质疏松进行及早的预防和诊治就显得十分必要。骨矿密度,即骨密度(BMD),是评定骨量减少,诊断骨质疏松的重要指标。目前,广泛使用的骨密度测量仪主要有利用X(γ)射线和超声波两类,其中双能X射线骨密度仪(以下简称骨密度仪或DXA)因测量结果的可靠性较好,而被视为骨密度测量的“金标准”。正常使用的骨密度仪需要有一定的测量范围以覆盖人体骨密度的变化,由于骨密度仪本身测量敏感性的原因,对于不同密度的测量误差并不相同,同时检定用模体的仿真程度和骨密度仪出厂时的刻度误差会引入系统误差。因此,在检定骨密度仪的过程中,可能遇到骨密度测量结果超差的情况。JJG1050-2009《X、γ射线骨密度仪》检定规程规定,允许对超差的测量结果进行线性校正,基于此,有必要对DXA骨密度测量结果线性校正值作不确定度分析评定。
1 测量过程
依据JJG1050-2009规定的检定方法和要求,在厂家规定的正常使用条件下,用HologicDiscovery A型双能X射线骨密度仪测量腰椎骨密度模体(简称腰椎模体)。测量用的腰椎模体由辐射等效固体水材料[由聚乙烯(C2H4)和少量氧化镁(MgO)及碳酸钙(CaCO3)组成]和等效骨材料[羟磷灰石Ca5OH(PO4)3]制成,腰椎模体有三个椎骨样品,其骨密度分别为 0.502g/cm2、1.005g/cm2和 1.501g/cm2。将腰椎模体放在测量床上,经定位后对椎骨样品进行连续n次测量,在所得扫描图像中画取感兴趣区(ROI),且每次ROI的画取均保持在椎骨样品的相同位置,骨密度仪可直接给出感兴趣区域的骨密度结果yij,其中i为椎骨样品序号(i=1,2,3),j为测量序号(j=1,2,…,n)。各椎骨样品骨密度的测量值Yi应为各样品n次测量结果的平均值,

表1为骨密度仪对腰椎模体中三个椎骨样品连续10次测量数据,表1中最后一列为各椎骨样品10次测量的平均值Yi,作为各椎骨样品的测量值。从表1中可以看出三个椎骨样品的测量值与标称值相差较大,测量值的相对误差分别为5.6%、-4.2%和-10.5%,特别是3号样品测量值的相对误差(-10.5%)已经超过了规程所允许的相对误差最大值(±10%),因此有必要对测量值进行线性校正后重新计算误差。
2 线性校正模型
根据线性回归原理,利用最小二乘法建立测量值与标准值之间的线性校正曲线,它们之间的校正方程表示为

表1 对模体中三个椎骨样品连续 10 次测量的数据单位:g·cm-2

式中:Y——椎骨样品测量值,g/cm2;
X——与测量值对应样品的实际值(标准值),g/cm2;
a——直线斜率;
b——截距,g/cm2
在制作校正方程时,X代表椎骨样品实际值,Y代表相应的仪器测量值;在利用校正方程时,X代表校正后的BMD值,Y代表未校正的测量值。由式(2)可得校正后的BMD值(Y*)和未校正的测量值(Y)的关系为

式(3)即为评定校正后的BMD值(Y*)不确定度的测量模型。对于不同椎骨样品的校正值,其由同一个校正方程得到,但由于测量结果的不同,各椎骨样品校正值的不确定度应引用各自的实际测量数据进行评定。
3 校正值不确定度的影响因素
由式(3)可知影响骨密度校正值不确定度的因素主要有:校正方程斜率a引入的不确定度u(a)和校正方程截距b引入的不确定度u(b),以及未校正的测量值Y引入的不确定度u(Y)。其中,u(a)和u(b)来自于线性回归方法求解校正方程的过程,u(Y)则来自于实验测量过程,其主要包括测量重复性引入的标准不确定度分量u1(Y)、模体引入的标准不确定度分量u2(Y)、仪器分辨力引入的标准不确定度分量u3(Y)和环境温度变化引入的标准不确定度分量u4(Y)。
4 骨密度线性校正
用线性回归分析对BMD测量值进行校正时,由骨密度仪对已知椎骨样品进行10次测量,每一个椎骨样品取10次测量结果的平均值作为仪器对该椎骨样品的测量值,再由最小二乘法作腰椎模体椎骨样品实际值与相应的仪器测量值的线性拟合,即可得到骨密度值线性校正方程。已知三个椎骨样品实际值输入量分别为X1、X2和X3,相对应的BMD测量平均值分别为Y1、Y2和Y3,可以得到(X1,Y1)、(X2,Y2)和(X3,Y3)三组数据,利用这三组数据即可得到校正方程。
式(2)是一种理想关系,实际输入Xi所对应的理想输出值Y(Xi)与测量值Yi间存在偏差εi,即

根据最小二乘法,a和b的值应能使εi的平方和(Q)最小,即
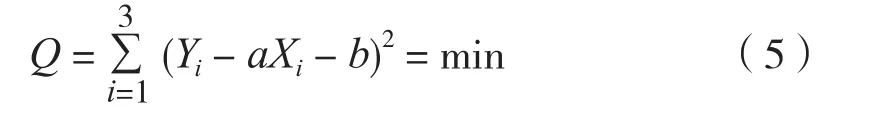
因此,令Q分别对a和b的两个一阶偏导数为零,即

解上述方程组的过程中无法得到a和b的真实值,而是估计值,因此,方程组(6)中的a和b分别用和替代,则可得到和相关的式(7)~(12),是它们的实验方差,是估计的相关系数。

式中:m=3,为椎骨样品数;

利用式(14)可得三个椎骨样品测量值对应的校正值及其相对误差,
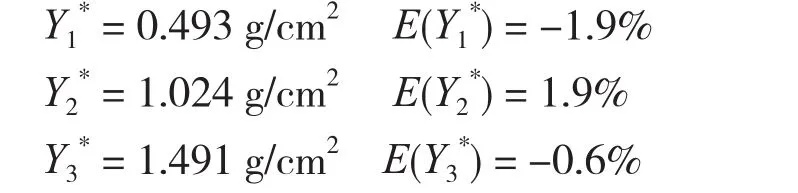
与校正前的结果进行比较可以发现,三个椎骨样品的相对误差均有大幅度的减小。从整体来看,相对误差范围由-10.5%~5.6%变为-1.9%~1.9%,校正值整体上更接近椎骨样品的标称值。
5 各分量标准不确定度的评定
5.1 校正方程斜率和截距引入的标准不确定度
由前文分析可知,线性回归方法得到的校正方程的斜率和截距为估计值,用和表示,它们的标准不确定度是它们的实验标准偏差,所以有
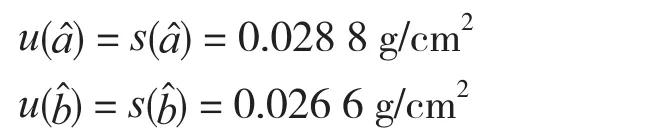
5.2 测量值 引入的标准不确定度
校正过程中使用的三个椎骨样品的测量值是各样品10次测量结果的算术平均值Yi,各椎骨样品测量值的标准不确定度应分开评定,u(Yi)表示第i号椎骨样品测量值引入的标准不确定度。
5.2.1 测量重复性引入的标准不确定度u1(Yi)
利用骨密度仪对被测模体进行10次独立重复测量,测量值为yij(j=1,2,…,10),其单次测量结果yik的实验标准偏差s(yik)可用贝塞尔公式计算,
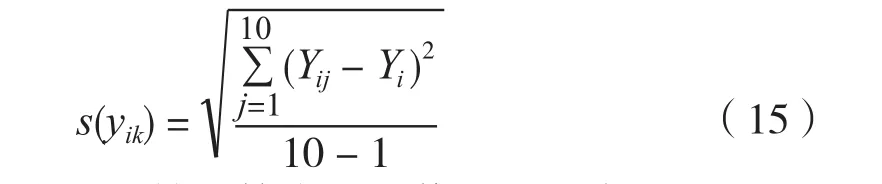
则10次测量结果算术平均值Yi由重复性引入的标准不确定度为

5.2.2 模体引入的标准不确定度u2(Yi)
标准模体的不确定度为0.5%(k=2),由溯源证书提供,则由模体引入的标准不确定度为
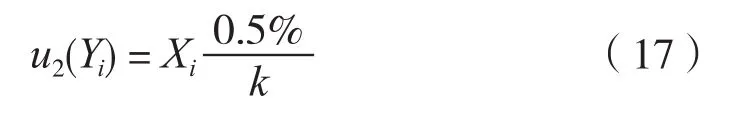
5.2.3 被测仪器分辨力引入的标准不确定度u3(Yi)
骨密度仪分辨力δ=0.001g/cm2,则区间半宽度为,可设为均匀分布,此时k取,则由仪器分辨力引入的标准不确定度为

5.2.4 环境温度引入的标准不确定度u4(Yi)
参考文献资料,本次测量的环境温度变化对模体骨密度的影响小于0.01%,因此,由环境温度引入的标准不确定度u4(Yi)可忽略。
5.2.5 骨密度测量值Yi的合成标准不确定度u(Yi)
由于上述几个分量不相关,合成标准不确定度u(Yi)可按式(19)计算
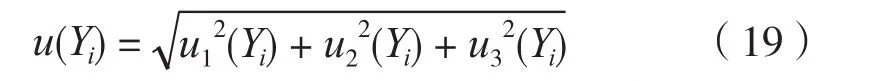
因此,三个椎骨样品的测量值的合成标准不确定度分别为

6 合成标准不确定度分析
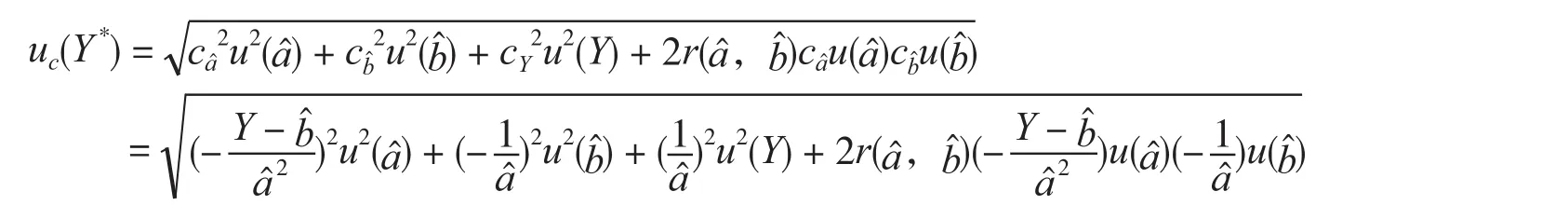
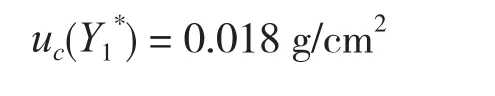
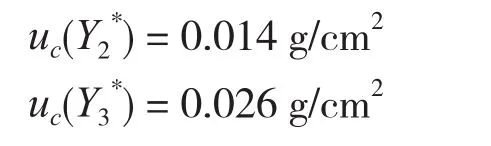
7 扩展不确定度的评定
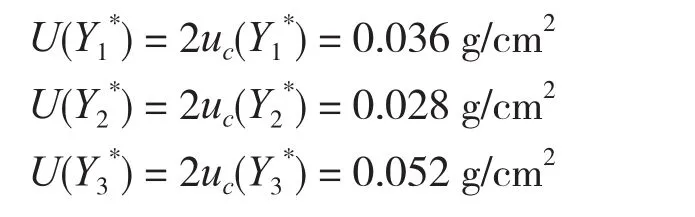
8 不确定度的报告
本例所评定的骨密度测量值线性校正值的不确定度报告如表2所示。
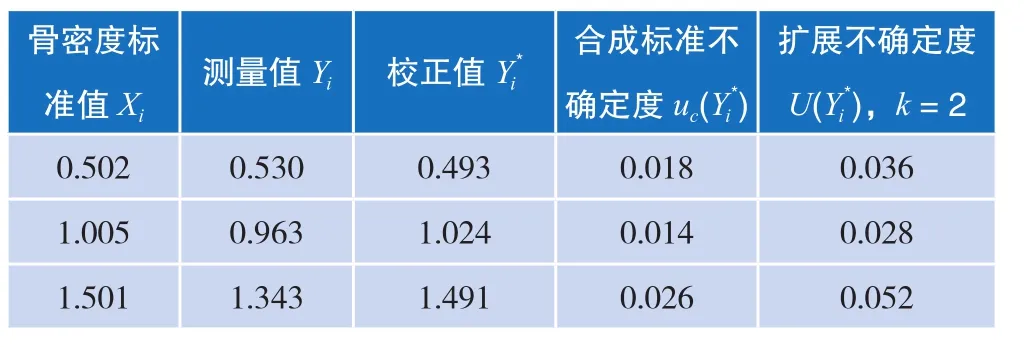
表2 校正值的不确定度报告单位:g·cm-2
9 结语
双能X射线骨密度仪作为医疗检验中最常用的骨密度测量仪器,其测量结果的可靠性尤为重要.对于超差的DXA骨密度测量值有必要进行线性校正,经线性校正后骨密度测量值的相对误差有了大幅度的减小,整体更接近标准椎骨样品的标称值。通过对校正值不确定度的分析评定,由各不确定度分量及其对校正值不确定度的贡献比较显示,校正值的不确定度受校正方程斜率、截距的影响较大。

