基于圆球模型推导重力加速度与纬度的关系式

任孝有

(北京市通州区潞河中学 北京 101100)

有意义的科学实践活动既是探究活动，也是科学模型的建构、分析、验证、评估和优化的过程[1].模型建构，是2017版《高中物理课程标准》中科学思维之一，是培养学生核心素养的重要方法，也是高考中重点考查的内容，例如2019年高考北京卷第24题对雨滴运动建构圆球模型、圆盘模型以解决不同的问题.在高三第二轮复习过程中，可以结合高中的典型问题，适度拓展，帮助学生体会模型建构的过程，促进建模能力的提升.

1 提出问题

重力加速度的大小随纬度的增加而增大，那么两者的定量关系是什么呢？为了解决这个问题，我们需要对地球形状进行建模，选择静止在地球表面上的小物体作为研究对象，分析其受力和运动，进而获得重力加速度的表达式.

2 建构模型

2.1 《普通物理学》中重力与万有引力的关系

在地球表面上的物体所受的万有引力F可以分解成物体所受的重力G和随地球自转而做圆周运动的向心力F′，如图1所示，其中

式中G0为万有引力常量.

F′=mω2r

地面上观察时，如图2所示，支持力N与G是一对平衡力，方向相反，而N与接触面垂直，从图1中F与G的方向关系分析，G不指向地心，N就不是背离地心，所讨论模型不是球形，而是椭球形状，赤道直径大于两极点间距离.高中阶段分析万用引力问题时，地球常简化为圆球，这样数学要求相对简单，更符合高中阶段学生的认知水平，因此需要建构圆球模型推导重力加速度与纬度的关系式[2].

图1 地球表面物体所受万有引力分解

图2 地面上的物体受一对平衡力

2.2 基于圆球模型推导重力加速度与纬度的关系式

按地球为圆球模型对静止在地面上的小物体m进行受力分析，如图3所示，指向地心的万有引力F，垂直切面向外的支持力N，同时必有一个沿切面向上的静摩擦力f，才能提供物体随地球做圆周运动的向心力.因此，更准确地说是建构表面粗糙的圆球模型.对于重力G，在地面上其大小等于物体所受的支持力N，方向沿半径指向地心O.

图3 地面物体受力分析

设地球半径为R，自转角速度为ω，在纬度α处，小物体m做圆周运动的轨道半径为r.如图3所示，建立水平竖直坐标系，对F，N，f进行正交分解有

将两个等式变换，消掉f

得

F-N=mω2rcosα

因为

r=Rcosα

所以

F-N=mω2Rcos2α

即

G=F-mω2Rcos2α

分两种情况做初步分析：

(1)两极时，α=90°，重力等于万有引力；

(2)赤道时，α=0，G=F-mω2R.

与常规分析一致.

进一步分析，显然对于任意纬度，重力加速度

(1)

取

G0=6.672 59×10-11N·m2/kg2

M=5.965×1024·kg

R=6 371 393 m

得到如表1所示对比数据.

表1 不同纬度对应的加速度

根据表1数据，用Excel画出重力加速度g与纬度α的关系图线如图4所示，从中可以看出计算值g小于查询值g0，但变化趋势一致.考虑到地球实际不是球形，结果需要修正，从图4猜想，如果将计算图线的起点与终点上移与查询值一致，两条图线或许会重合.

图4 g-α关系图

3 修正模型

因为式(1)右侧两项中都含有半径R，基于控制变量的思想，保持R不变.G0为万有引力常量不能改变，因此第一项中只能改变M，第二项只改变ω.根据查询数据可得以下结论.

当α=90°时，g极点=9.832 18 m/s2，代入式(1)有

(2)

当α=0时，g赤道=9.780 30 m/s2，代入式(1)有

(3)

联立式(2)、(3)可得

ω2R=0.051 88 m/s2

(4)

由式(1)、(2)、(4)得出g的一般表达式

g=(9.832 18-0.051 88 cos2α)m/s2

(5)

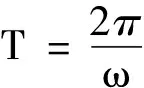
表2 不同纬度对应的修正后的重力加速度

图5 修正后的g-α关系图

4 评估模型

查询资料[4]，当把地球看成是一个球体近似有

g=9.780 3×(1+0.005 3sin2α)m/s2

(6)

根据式(5)、(6)获得的数据，同样画出g与α的关系图线，如图6所示，两者完全重合，说明修正的关系式(5)成立，所建构圆球地球模型成立.

图6 把地球看成一个球体g-α关系图

5 应用模型

按照资料[4]，当把地球看成是一个椭球时，有

g=9.780 3×(1+0.010 5sin2α)m/s2

(7)

由式(7)可知

α=0g赤道=9.780 3 m/s2

α=90°g极点=9.883 0 m/s2

按照式(1)及修正过程，可以得到

g=(9.883 0-0.102 7cos2α)m/s2

(8)

根据式(7)、(8)获得的数据，画出g与α的关系图线，如图7所示，两者完全重合，说明修正的关系式(8)成立.

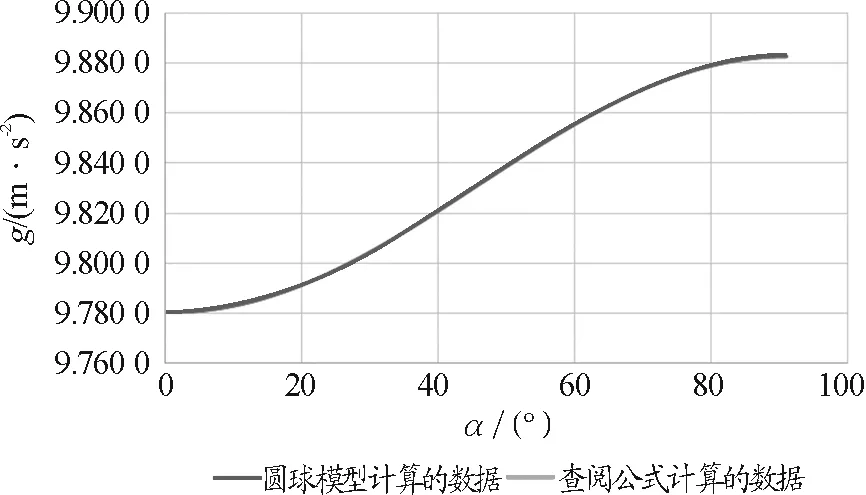
图7 把地球看成一个椭球体g-α关系图

也就是无论按哪种模型方法推导，只要按照上述建模及修正方法，都可以获得重力加速度g与纬度α对应的准确关系式.因此对于任意近似球状天体，只要精确测出两个不同维度上的重力加速度，则可以获得其重力加速度与纬度的关系式，而不需要其具体的质量、自转周期、半径等.如果使用赤道和极点的重力加速度，则重力加速度与纬度的关系可以表达为如下关系式

g=g极点-(g极点-g赤道)cos2α

6 反思模型：为何可以这样做？

圆是特殊的椭圆，圆球是特殊的椭球.从圆球推理出的重力加速度g的表达式，从椭球也应可以推出，但一定有不同，体现在修正前变化趋势类似而结果偏小，当然这种模型建构过程，更像是黑体辐射导致普朗克提出能量子，要充分借助实验数据，大胆想象，充分检验.