三阶带p-Laplacian算子边值问题正解的存在性

李永娜

（广东工业大学应用数学学院，广东广州510520）

本文研究了关于一维p-Laplacian算子边值问题

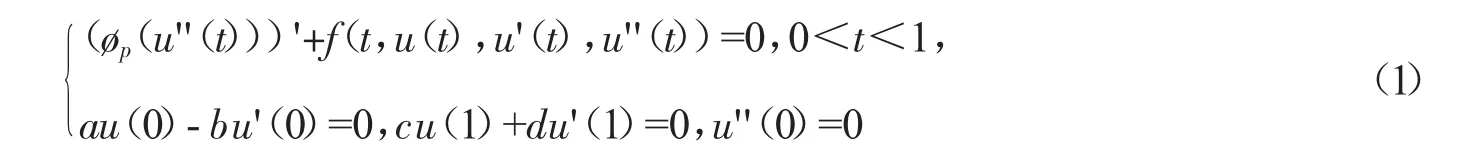
可以发现很多难题都可以转变成适当的微分方程来化解，比如人们一直所探讨的宇宙天体、量子力学、弹性理论、医学问题等。由于非线性问题更具有理论意义和应用背景，所以近些年，关于非线性边值问题越发引起学术界的关注。

2008年，文献［1］表明了三阶边值问题

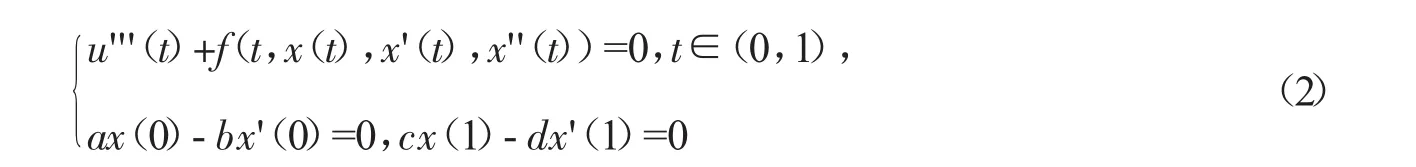
解的情况。借助于上下解和Schauder不动点定理，给出了至少存在一个解的充分条件。

在很多不同的领域，带p-Laplacian算子的微分方程使用非常广泛。到目前为止，关于带p-Laplacian算子的研究已不胜枚举［2-8］。虽然p-Laplacian算子边值问题解存在性的研究很多，但是大部分文献中的非线性项是含有一阶导数或二阶导数或不含导数项［9-11］。本文研究的新颖之处就在于：把边值问题（2）这种同时含有一阶导数和二阶导数的三阶微分方程推广到带p-Laplacian算子的三阶微分方程上来；不同于问题（2）中所用到的方法，本文采用Krasnosel’skill’s不动点定理给出了边值问题（1）至少含有一个正解和至少含有两个正解的充分条件。

1 预备知识

定义1［12］设E是Banach空间，K是E中的非空闭集，如果K满足：

（1）任给 x，y∈K，α≥0，β≥0，有 αx+βy∈K；

（2）若 x∈K，x≠θ，则-x∉K。则称K是E中的锥。

定义2 ω是一个凹函数，如果

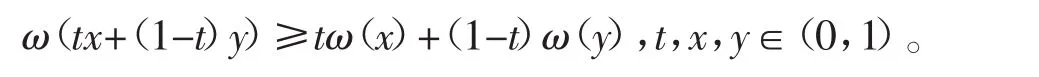
引理1［13］设E是一个实Banach空间，K∈E是E中的一个锥，假设Ω1，Ω2为E中的有界开集，并且是全连续算子，如果下列条件之一成立：

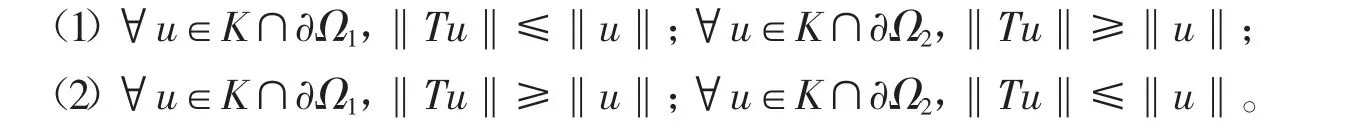
则T在K∩（Ω2Ω1）中有一个不动点。

下面需要用一些初步的结果去证明文中的主要结果，首先，给出关于二阶边值问题

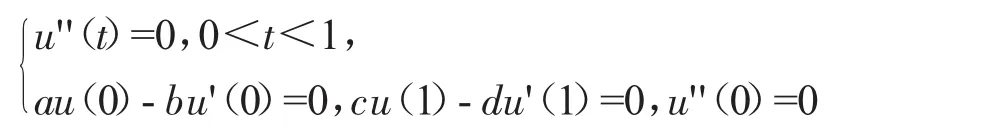
的格林函数，即

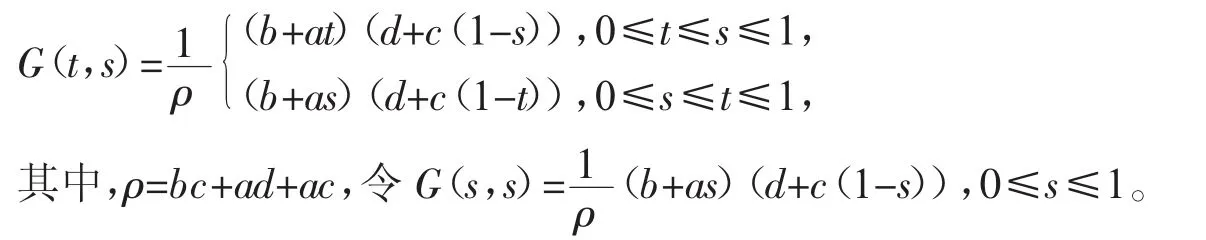
不难看出，格林函数G（t，s）具备如下性质：

（1）对于任意的 t，s∈（0，1）＜1，都有

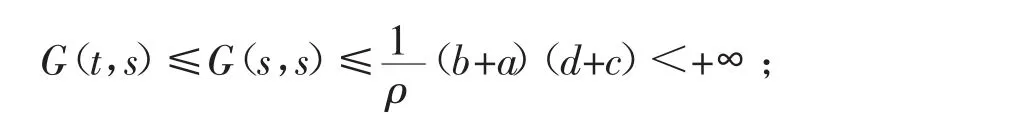
在本文中，假设下面前提是成立的：

（H）f∈C（［0，1］×［0，+∞）×R×（-∞，0］，［0，+∞））。

为了方便，引用以下记号

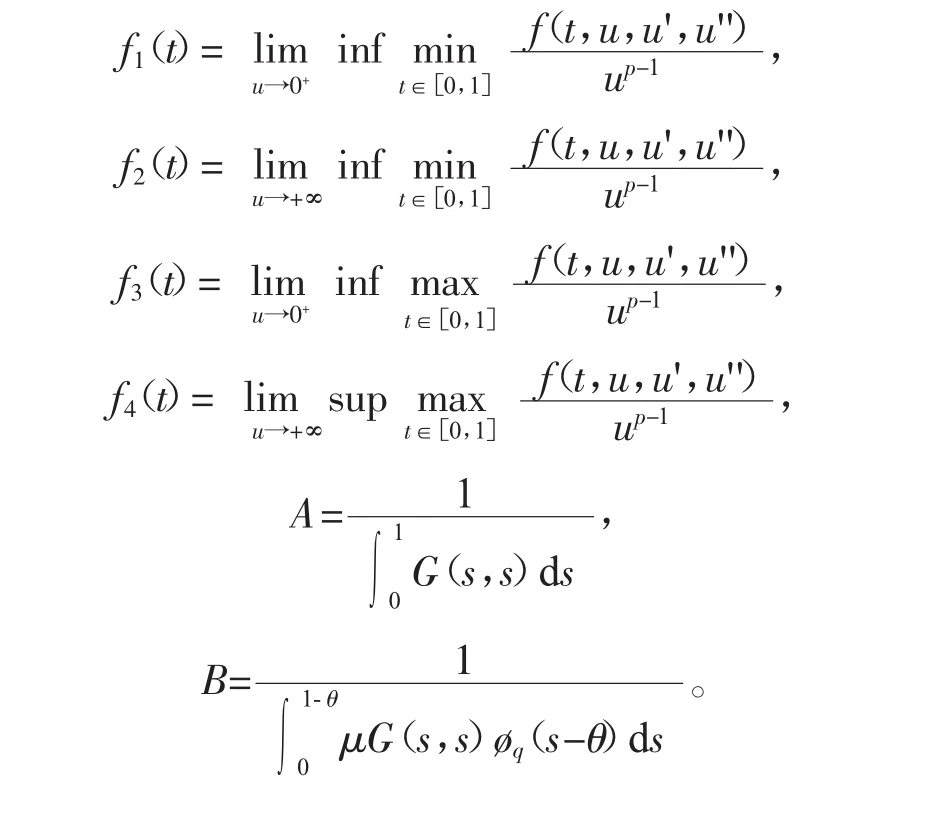
接下来，在Banach空间中，令E=C2［0，1］，E中范数定义为最大范数，即

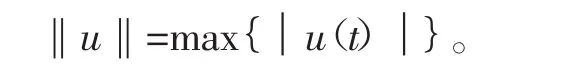
令锥K=｛u∈C+［0，1］│u是凹函数｝，其中C+［0，1］=｛u∈C+［0，1］│u（t）≥0，t∈［0，1］｝。

定义一个积分算子T：K→C+［0，1］，

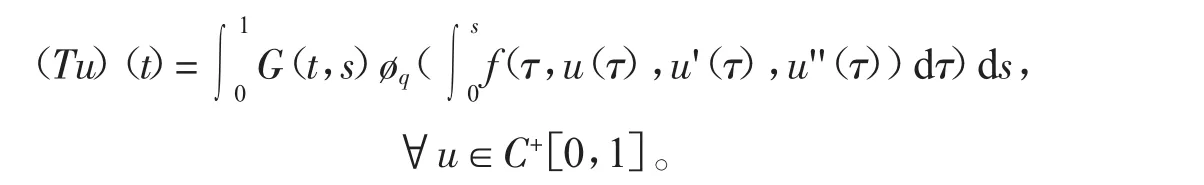
显然（Tu）（t）≥0，t∈［0，1］｝。

引理2 TK∈K，且T的不动点是边值问题（1）的解。

证明 如果存在u是算子方程Tu=u的解，得到

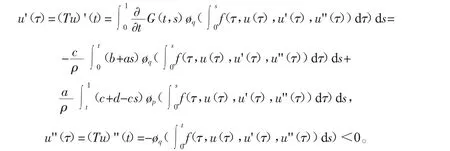
此外

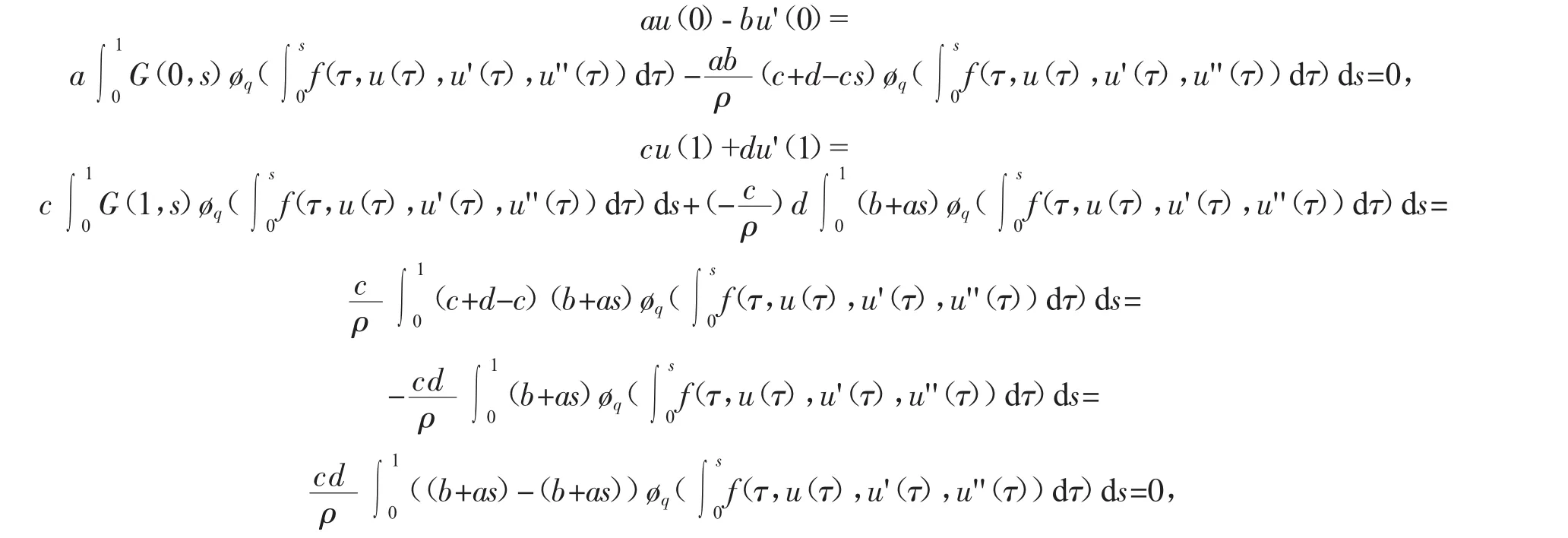
并且，u''（0）=0。所以，T的所有不动点都是边值问题（1）的解，证毕。

引理3 假设（H）成立，则T：K→K是全连续的。

证明 先证T是紧算子。首先，设T∈K是有界集，在D中有‖u‖=max｛│u（t）│｝，‖u'‖=max｛│u'（t）│｝，‖u''‖=max｛│u''（t）│｝，令‖│u│‖=max｛‖u‖，‖u'‖‖u''‖｝，则m=sup｛‖│u│‖：u∈D｝，从而‖u‖≤m，‖u'‖≤m，‖u''‖≤m。因为 f：［0，1］×［0，+∞）×R2→［0，+∞）是连续的，可知在有界闭集［0，1］×［0，m］×［-m，m］×［-m，0］上f（t，u（t），u'（t），u''（t））能取到最大值［14］。

因为D∈K是有界集，故存在M0＞0，使得‖u‖＜M0＜m。对任意的u∈D，有

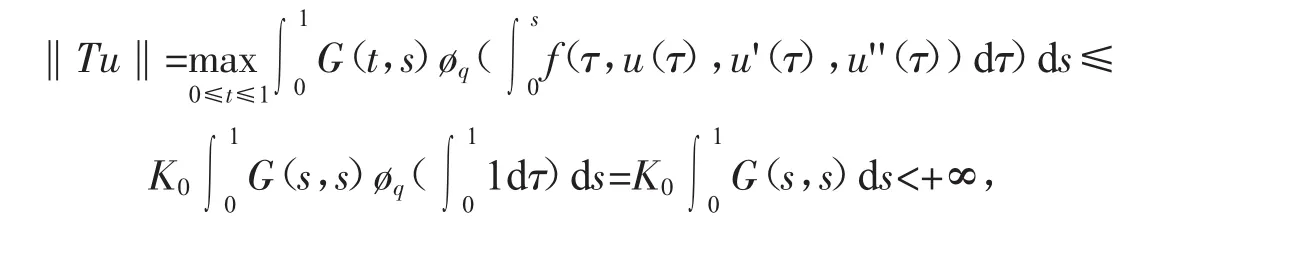
其次，对任意的 t∈（0，1），有

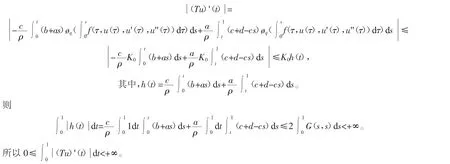
因此，T（D）是等度连续的。根据 Ascoli-Arzela’s定理［15］知 T（D）是相对紧集。

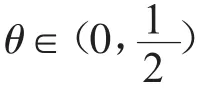
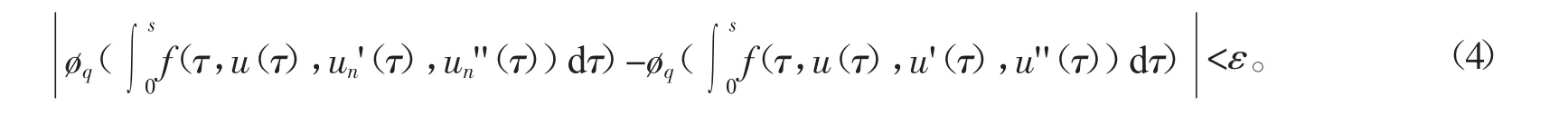
因此，对任意的 n＞n0，t∈（0，1），由式（3）和（4）可得

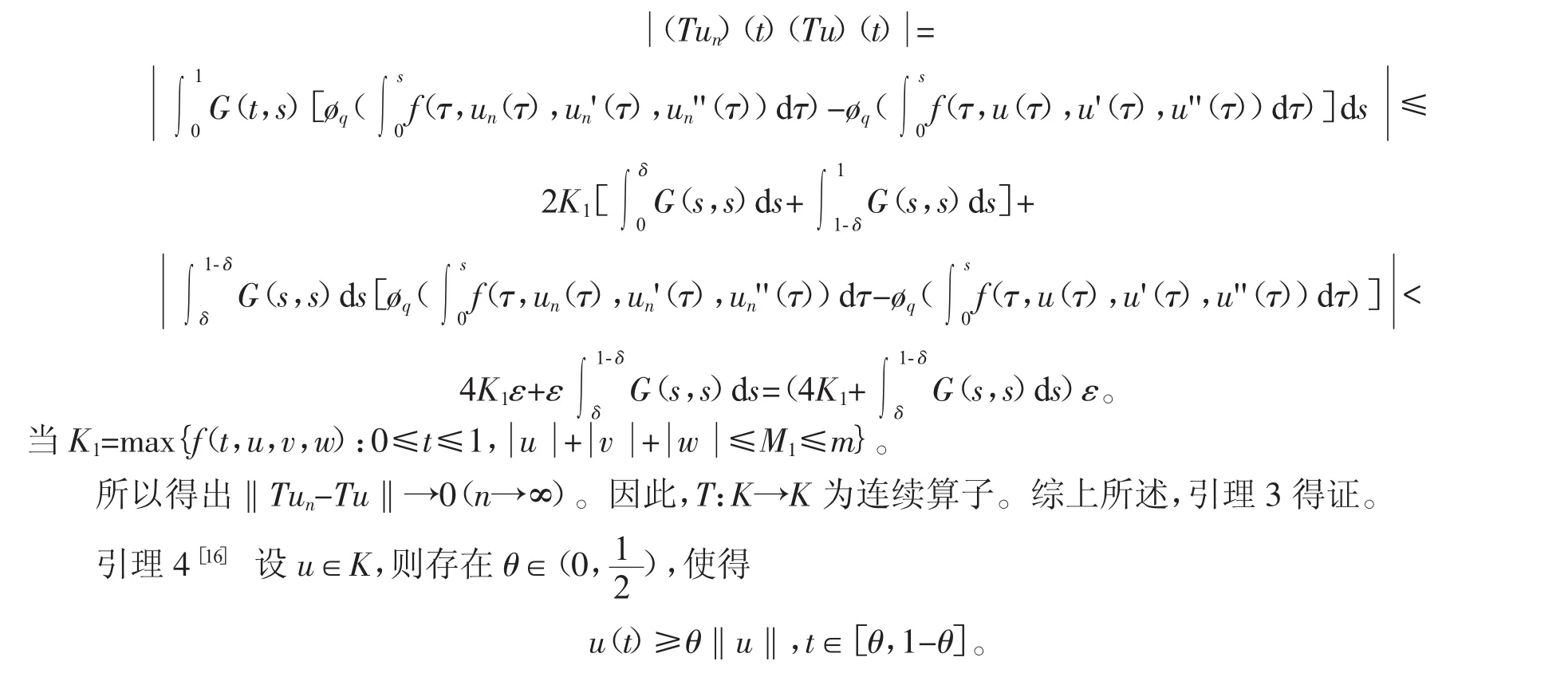
2 主要结果

定理1前提（H）假设成立，如果符合下面两种情况：

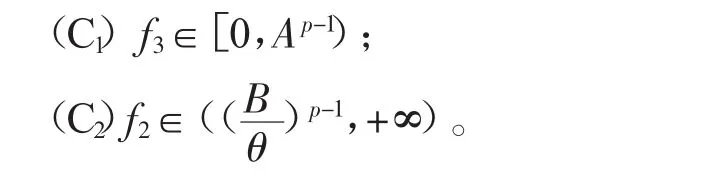
则边值问题（1）至少存在一个正解。

由式（5）、（6）和引理 1知，算子 T 有不动点 u∈K∩（Ω2Ω1），则边值问题（1）至少存在一个正解 u。

类似于定理1的方法，不难获得定理2的结果。

定理2前提（H）假设成立，如果符合下面两种情况：

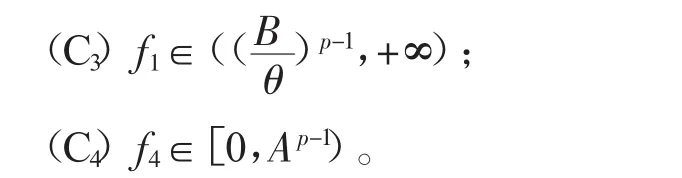
则边值问题（1）至少存在一个正解。

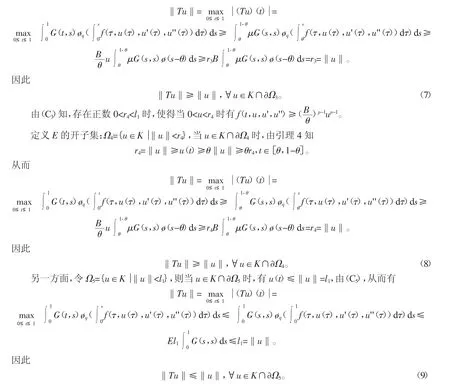
由式（7）～（9）知，算子 T 有不动点 u1∈K∩（Ω3Ω5），另一个不动点 u2∈K∩（Ω5Ω4），则边值问题（1）至少存在两个正解u1和u2。

类似于定理3的方法，不难获得定理4的结果。

定理 4 前提（H）和（C1），（C4）假设成立，如果还符合情况：

（C6）存在常数 F∈［B，+∞）和 l2＞0，使得

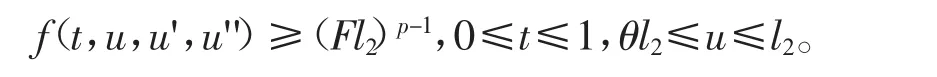
则边值问题（1）至少存在两个正解。