10折交叉验证用于预测模型泛化能力评价及其R软件实现
梁子超 李智炜 赖 铿 林卓琛 李铁钢 张晋昕
1 中山大学公共卫生学院医学统计学系,510080 广东 广州;2 广州市结核病防治所,510095 广东 广州
泛化能力是指模型在训练集上训练后,对新数据进行准确预测的能力。交叉验证(cross-validation,CV)则是一种评估模型泛化能力的方法,广泛应用于数据挖掘和机器学习领域[1]。在交叉验证中,通常将数据集分为两部分,一部分为训练集,用于建立预测模型;另一部分为测试集,用于测试该模型的泛化能力。
在应用交叉验证评估模型泛化能力的过程中,最关键的因素是选择划分训练集和测试集的比率,当训练集样本量过小时会引发过拟合。在如何划分2个集合的问题上,统计学界提出了多种方法:简单交叉验证(holdout cross-validation)、留一交叉验证(leave-one-out cross-validation,LOOCV)、k折交叉验证(k-fold cross-validation)、多重k折交叉验证、分层法(stratification-split cross-validation)、自助法(bootstraps)等。
简单交叉验证将原始数据随机分为2个集合,分别作为训练集和测试集,但其最终所得结果与集合划分比率密切相关,不同划分比率结果变异可能较大。该方法在总数据集并不是非常大的情形下很难达到准确评估模型的目的。留一交叉验证是指,假设在总集合中共有n个个体,每次选取1个个体作为测试集,其余个体作为训练集。总共进行n次训练,取平均值作为最终评价指标。留一交叉验证较为可靠,在每次模型训练中纳入几乎所有个体,当总集合中个体数目较多的情况下计算时间较长。k折交叉验证则是将原始数据随机平均分为k个子集,每个子集做测试集的同时,其余k-1个子集合并作为训练集,进行k次训练,取各评价指标(灵敏度、特异度、AUC等)的平均值。该方法可以使用数据集中的所有样本进行预测,通过平均的评价指标来降低奇异的训练集和测试集划分方式对预测结果的影响。k值的选取对最终结果也有一定影响,有研究表明k值越大则评估准确性越高,当k为5或10时在评估准确性和计算复杂性下综合性能最优[2]。
本文介绍10折交叉验证的基本原理,使用R语言在实例中展示10折交叉验证的实现方法。
1 10折交叉验证基本原理
10折交叉验证是指将原始数据集随机划分为样本数量近乎相等的10个子集,轮流将其中的9个合并作为训练集,其余1个作为测试集。在每次试验中计算正确率等评价指标,最终通过k次试验后取评价指标的平均值来评估该模型的泛化能力。
10折交叉验证被广泛应用于医学领域中的机器学习研究,作为一种测试集与训练集划分的方法。有研究者使用10折交叉验证方法评价支持向量机算法利用影像学资料对新型冠状病毒肺炎(COVID-19)的预测能力[3]。也有研究者利用支持向量机和稀疏贝叶斯极限学习机算法,在10折交叉验证下使用脑电图信号预测疼痛及疼痛出现的位置[4]。此外,也有研究者使用LASSO回归算法及10折交叉回归方法,通过长非编码RNA(lncRNA)表达情况预测宫颈癌患者复发的风险[5]。
10折交叉验证的基本步骤如下:
(1)原始数据集划分为10个样本量尽可能均衡的子集;
(2)使用第1个子集作为测试集,第2~9个子集合并作为训练集;
(3)使用训练集对模型进行训练,计算多种评价指标在测试集下的结果;
(4)重复2~3步骤,轮流将第2~10个子集作为测试集;
(5)计算各评价指标的平均值作为最终结果。
10折交叉验证的原理示意见图1。
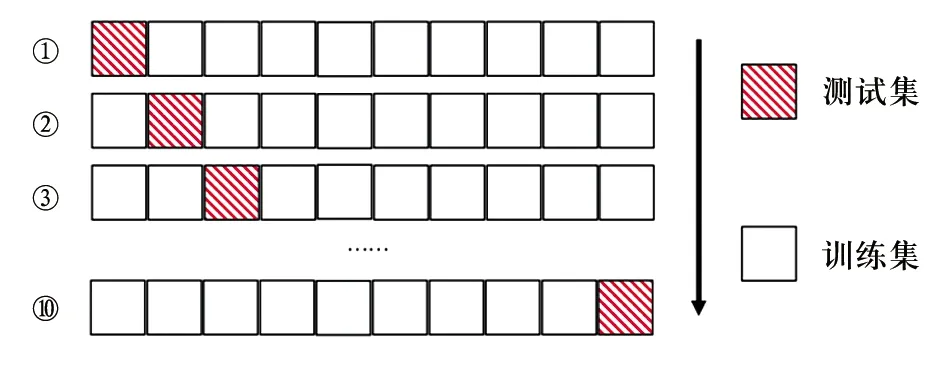
图1 10折交叉验证的原理示意图
2 实例分析
下面结合实例展示10折交叉验证的具体实现方法。所有统计分析均使用R软件(版本3.6.3)进行。其中k折交叉验证使用caret包,绘制ROC曲线使用pROC包。
实例数据来源于广州市胸科医院2014年1月至2017年12月中所有被诊断为利福平耐药结核病(rifampicin drug-resistant tuberculosis,RR-TB)、耐多药结核病(multidrug-resistant tuberculosis,MDR-TB)或广泛耐多药结核病(extensively drug-resistant tuberculosis,XDR-TB)的患者治疗前的基本人口学信息及部分临床检查结果,共387人次。
自变量包括年龄(<18岁、18~岁、30~岁、60~岁),性别,户籍类型(本地、市内流动、外来流动),患者登记分类(新患者、初治失败、复发、复治失败),4种药物耐药性[isoniazid(INH)、rifampicin(RFP)、ethambutol(EMB)、streptomycin(SM)],诊断结果(RR/MDR/XDR-TB),抗结核一、二线药物使用情况(无、仅使用一线药、使用过一线和二线药),是否在治,治疗模式(门诊、住院),使用药物类型[国产,绿灯委员会(Green Light Committee,GLC)],治疗时长(≤180 d、180 d~、360 d~、不详),痰涂片结果(全程为阴性、阴性和阳性均出现过、全程为阳性),痰培养结果(全程为阴性、阴性和阳性均出现过、全程为阳性);因变量为治疗结局(治愈、治疗失败)。
2.1 建立模型并计算评价指标
建立预测模型前对所有自变量进行单因素分析(使用χ2检验,当理论频数<1时,使用Fisher确切概率法,检验水准α=0.10),将单因素分析有意义(户籍类型,抗结核一、二线药物使用情况,使用药物类型,痰涂片结果,痰培养结果)和既往研究[6-8]提出的危险因素(年龄,登记类型,抗结核一、二线药物使用情况,治疗时长)作为自变量纳入模型中,自变量中所有多分类变量均作为哑变量纳入模型。使用逐步回归法进行自变量筛选(纳入水准为0.05,排除水准为0.10),筛选后最终仅纳入户籍类型和登记类型两自变量进入预测模型。
在预测中,截断值的确定是基于约登指数最大的法则。分别计算5折、10折、20折交叉验证下的平均正确率、灵敏度、特异度、AUC值和程序运行时间。分别使用10个种子计算5、10、20折交叉验证所得评价指标平均值的标准误。得出10折交叉验证下的10条ROC曲线及10次所有预测值与其对应的观测值合并所得出的融合ROC曲线,同时将10折交叉验证下10次所有预测值与其对应的观测值融合后与留一交叉验证方法得出的评价指标进行比较。这里的融合就是把k折交叉验证的k轮预测结果放在一起,进而可以联合起来计算出该验证方法的统一灵敏度、特异度等指标值。
10折交叉验证的关键代码见表1。

表1 10折交叉验证的关键代码
2.2 预测结果
10折交叉验证下平均正确率为0.750(95%CI:0.659~0.841)、灵敏度为0.732、特异度为0.771、AUC为0.707;ROC曲线及融合ROC曲线见图2。不同训练集和测试集的划分下各模型评价指标的波动较大。正确率的极差为0.455,四分位数间距为0.107;灵敏度的极差为0.471,四分位数间距为0.250;特异度的极差为0.600,四分位数间距为0.222;AUC的极差为0.448,四分位数间距为0.066。
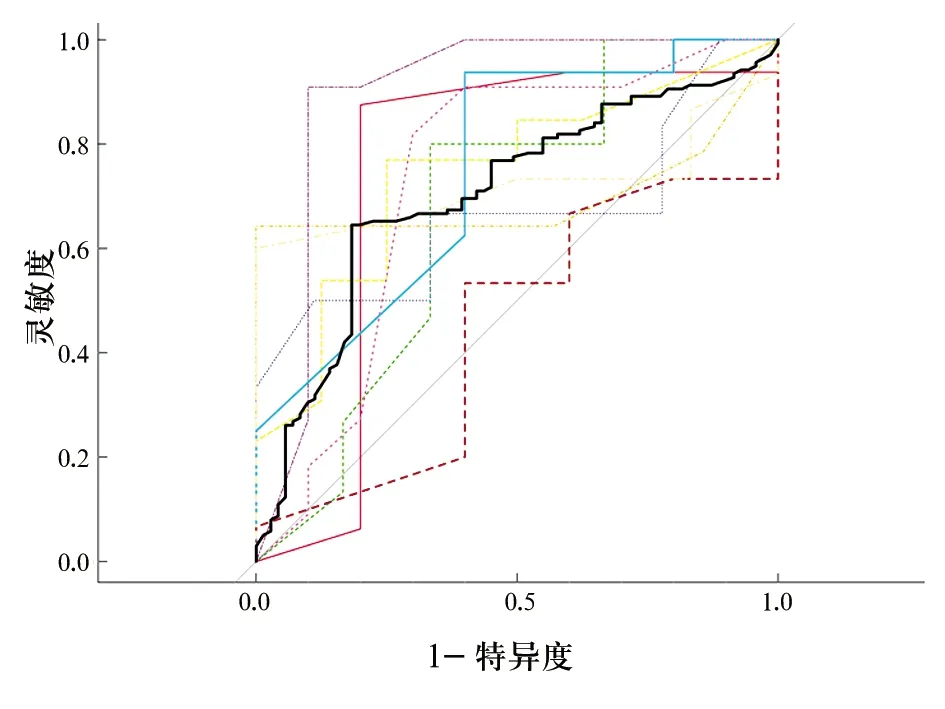
图2 10折交叉验证下的ROC曲线及融合ROC曲线
实例中10折交叉验证法在平均正确率和灵敏度中均高于5折与20折交叉验证法。20折相较于10折而言计算复杂度增加的同时对评价指标的变化并不明显,平均正确率降低0.037,平均AUC提高0.029。将10折交叉验证中10次预测值与其原始观测值融合后与留一验证法进行比较,正确率、灵敏度和特异度相同且AUC差别不大,但程序运行时间明显增加。从结果也可看出,随着折数的增加程序运行时间也明显增加。使用10个种子计算5、10、20折交叉验证所得评价指标平均值的标准误后可知,随着折数增加各评价指标的标准误也在增大。综合以上结果可知,10折交叉验证在提高各项评价指标的同时,稳定性与运行效率的损失相对较低。
实例中10折交叉验证中10次训练所得评价指标及平均值见表2;5、10、20折交叉验证所得评价指标的平均值见表3;分别使用10个种子计算5、10、20折交叉验证所得评价指标平均值的标准误见表4;10折交叉验证中10组数据融合及留一交叉验证法所得评价指标见表5。

表2 10折交叉验证中10次训练所得评价指标及其平均值

表3 5、10、20折交叉验证所得评价指标的平均值

表4 5、10、20折交叉验证评价指标的标准误(基于10个种子)
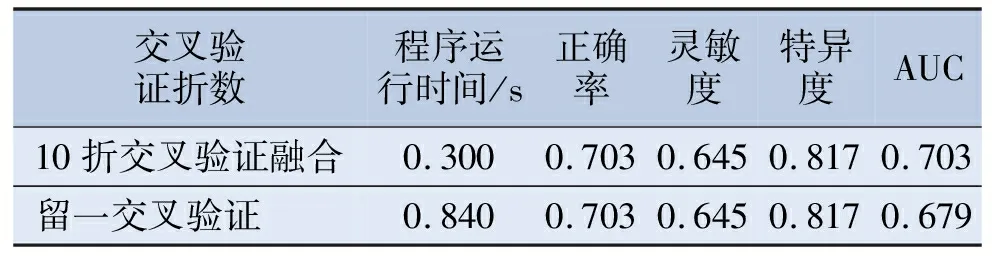
表5 10折交叉验证融合与留一交叉验证的对比
3 讨论
本文介绍了10折交叉验证的原理和在R语言环境下的实现方法,用实例说明不同的训练集和测试集划分对模型预测评价指标的影响。相较于其他交叉验证方法,10折交叉验证能准确刻画模型的泛化能力,稳定性与运行效率更佳。
10折交叉验证在实践中存在的局限性在于,当样本量较少时,将该样本随机分为10份会导致每次使用的训练集变化较大,导致最终10组评价指标的变异程度相对较大。当样本量较大时,使用10折交叉验证方法会导致模型计算复杂度增大且计算时间较长。当样本量非常大时,可直接采用简单交叉验证。当样本量较少或数据不平衡程度较强时,可能会出现其中某次训练集中只有单一预测结局的情况,此时应减小折数,重新随机划分子集,采用分层法进行交叉验证或使用自助法进行验证。同时,使用10折交叉验证时,应预设种子以便结果可重现。
10折交叉验证被广泛应用于多种机器学习模型中,除本文介绍的logistic模型外,在LASSO回归、支持向量机、决策树、朴素贝叶斯分类、随机森林等多种模型中也可应用。STATA、SAS及MATLAB中均可使用10折交叉验证方法。

