基于样本优化的神经网络方法在储层裂缝识别中的应用

蓝茜茜, 张逸伦, 康志宏*

(1.中国地质大学(北京)能源学院，北京 100083；2.北京大学地球与空间科学学院，北京 100871)

随着非常规油气资源勘探开发需求不断增长，储层评价显得尤为重要[1]。非常规储层一般由于储层埋深大、储集空间复杂多变、储层物性非均质性强等原因，导致储层评价难度大。现有的储层评价方法无法精确表征油气藏，给勘探开发带来了极大的困难。对于裂缝发育的非常规储层，准确识别和预测裂缝发育程度对储层评价和油气开发起着举足轻重的作用。

目前，常规测井解释方法是主流的裂缝识别方法，但对于非常规储层裂缝的识别存在着识别率低、误差较大的问题。测井曲线分辨率较低且测井响应易受其他条件如充填物、泥浆、溶蚀作用等因素的影响；且在资料解释过程中通常以线性方法为运算基础，而实际地下储层情况复杂多变，简单的线性模型无法精确识别和表征裂缝发育程度。成像测井方法识别裂缝效果明显优于常规测井方法，但成本过高，获得的资料有限[2]。因此，如何在保证识别率的同时降低成本成为储层裂缝识别的难点。

人工神经网络方法最早由Caianiello等[3]提出，是一种常用的非线性数据挖掘算法，有较强的抗干扰能力、较好的系统容错性，后人对其进行了大量的算法改进和应用[4]。关于人工神经网络方法应用于油气资源储层评价前人已开展大量的工作[5-13]。曹思远等[5]运用BP(back propagation)神经网络法分析七个地震属性特征，并预测单井油、气、干层情况；潘和平等[6]依次采用BP神经网络法、奇异值分解法和灰色聚类法对低阻油气层进行识别，综合分析含水饱和度和电阻率等参数，判别储集层特性，其中BP神经网络方法识别效果最好；杨志力等[7]运用BP神经网络法综合三条测井曲线对声波曲线进行重构，以此增加测井曲线的信息量，并提高了受井壁垮塌影响的声波测井曲线的质量；Xue等[8]结合遗传算法和BP神经网络法预测裂缝发育程度，克服了BP算法易陷入局部极小值的缺点。

为了克服线性运算的缺点，使裂缝识别结果更加接近实际储层，采用基于非线性运算的BP神经网络法，以塔河油田碳酸盐岩储层的一口探井为例，利用常规测井参数和成像测井结果建立神经网络模型，对储层裂缝发育情况精准预测。在建立神经网络模型时，学习算法、网络结构、样本选取等因素都会对最终模型结果产生影响，前人在算法和网络结构等方面进行了大量的改进，但关于样本选取问题研究较少。由于训练样本间参数的差异较大，如果笼统地将所有样本作为输入建立神经网络模型，则会导致模型不够准确。为此，引入聚类方法优化样本，采用K-means算法对原始样本聚类，并在每类中选取代表性样本分别建立神经网络模型，最后对碳酸盐岩储层裂缝密度进行精准预测。

1 测井曲线响应特征与相关性分析

储层评价通常采用多种测井解释方法，但各种测井资料对储层裂缝发育的敏感度不同，其对应的响应特征也不同[14]。以塔河油田碳酸盐岩储层A探井为例，选取5 450～5 700 m井段进行分析。采集的常规测井资料有；声波时差曲线(AC)、自然伽马曲线(GR)、自然电位曲线(SP)、补偿中子曲线(CAL)、井径曲线(CNL)、浅侧向电阻率曲线(RS)、深侧向电阻率曲线(RD)和密度曲线(DEN)，如图1所示。在进一步处理前，先对测井曲线进行平滑滤波预处理，消除部分由于非地层因素诱发的干扰信息。

碳酸盐岩导电性极差，为高阻地层，裂缝发育处钻井液侵入，导致深、浅侧向电阻率测井曲线值均变小且两者变化幅度相似，但并未出现明显的正差异或负差异。裂缝填充程度不高，自然伽马测井曲线起伏较小。裂缝发育导致井径扩大，进而引起泥浆入侵形成泥饼，井径测井曲线值变小。当裂缝出现时，声波时差测井值突然增大，出现周波跳跃现象。由于裂缝影响，密度测井仪器不能很好地贴合井壁，导致密度测井值降低。中子测井曲线在裂缝发育处略微减小。裂缝张开，地层水入侵，产生电动势，自然电位测井变大[15-17]。

相较于常规测井方法，成像测井能更直观地识别裂缝。致密碳酸盐岩为高阻岩性，在成像测井图像上整体高亮；裂缝发育处被泥质填充，成像测井图像上表现为一条暗色正弦波曲线(图1)，根据成像测井图像可以定量识别出裂缝数量[18-19]。利用成像测井得到的裂缝数量散点数据，对其进行深度插值，最终得到裂缝密度(单位深度的裂缝条数)随深度变化的展布情况。

通过定性的常规测井曲线响应分析并不能准确表征测井参数和裂缝发育程度之间的关系。不同测井参数对裂缝发育程度的敏感性存在差异，若个别参数由于本身对裂缝发育程度的低敏感性，或测井记录时出现异常导致数据无效等原因，会严重影响后续神经网络建模的准确性。因此，通过相关性定量分析，剔除与裂缝发育相关性较差的参数，保留相关性较好的参数用作后续训练样本输入参数。

如图2所示，采用线性回归法建立各测井参数值与裂缝密度之间的定量关系。从图2总体来看，单个测井参数与裂缝发育程度相关性均较差，说明仅通过单个测井曲线无法准确识别裂缝密度。其中声波时差和密度测井参数相关系数明显低于其他测井参数，将其剔除。最终选定自然伽马、自然电位、补偿中子、井径、深侧向电阻率及浅侧向电阻率这6个参数进行BP神经网络建模。

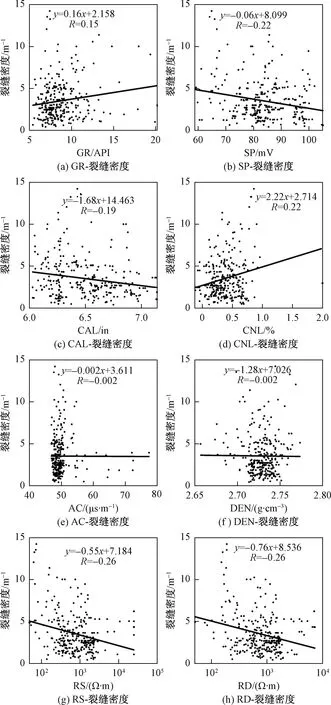
图2 测井参数与裂缝密度相关性分析

2 BP神经网络模型

BP神经网络法又称误差逆向传递算法，如图3所示，网络结构包括输入层、隐含层(一层或多层)和输出层，它模仿生物神经元，每一层传递的信号只作用于下一层，同层内节点无信号传输，具有良好的非线性运算能力。该方法包括信号正向传递和误差反向传递两个过程：①设置初始输入参数、初始传递权值和输出误差阈值，信号从输入层出发，经隐含层传向输出层，并计算输出结果与目标值的误差；②若误差大于设定阈值，则需要将误差由输出层反向传递到输入层，并根据梯度下降法传递误差调整权值，不断迭代上述过程，直到误差小于设定阈值，训练停止，输出神经网络模型参数。

图3 BP神经网络模型结构

2.1 样本优化——K-means聚类

前人在建立神经网络模型时将所有样本作为输入，这样做会导致最终模型过于“笼统”，无法准确表征各样本特征，模型预测结果较差。若将所有样本按照一定的相似度准则进行分类，并分别建立神经网络模型，此时模型更加细化”，分辨率提高，预测结果更加准确。因此，引入聚类算法进行样本优化。

聚类分析是一种无监督式学习策略，基于一定原则将样本进行聚类，其中K-means法是最常用的算法之一。该算法基于样本间距离进行聚类，样本间距离越近，相似度越高，越容易被划分为同一类，由于其具有易于实现，计算效率高的优点而被广泛使用[20]。

K-means算法也存在若干缺陷，如容易受奇异点干扰导致聚类结果变差，在聚类前需要提前根据实际样本指定类别个数等[21]。因此，聚类前需要先剔除部分奇异值样本；在确定类别个数时，应反复试验，保证类间距离大小在合适的范围内，通过测试最终将样本(均来自于塔河油田A探井)聚为三类。具体实现步骤为：①对所有神经网络训练样本(共计308 个)的测井参数进行归一化处理，部分数据如表1所示；②随机挑选3 个样本作为初始聚类中心(质心)；③分别计算各样本到各聚类中心的距离(欧式距离)，并将各样本划分到距离最近的类中；④每次聚类后重新计算各类的聚类中心，重新将样本聚类；⑤不断迭代，直到每类的聚类中心均不再发生改变时停止迭代。

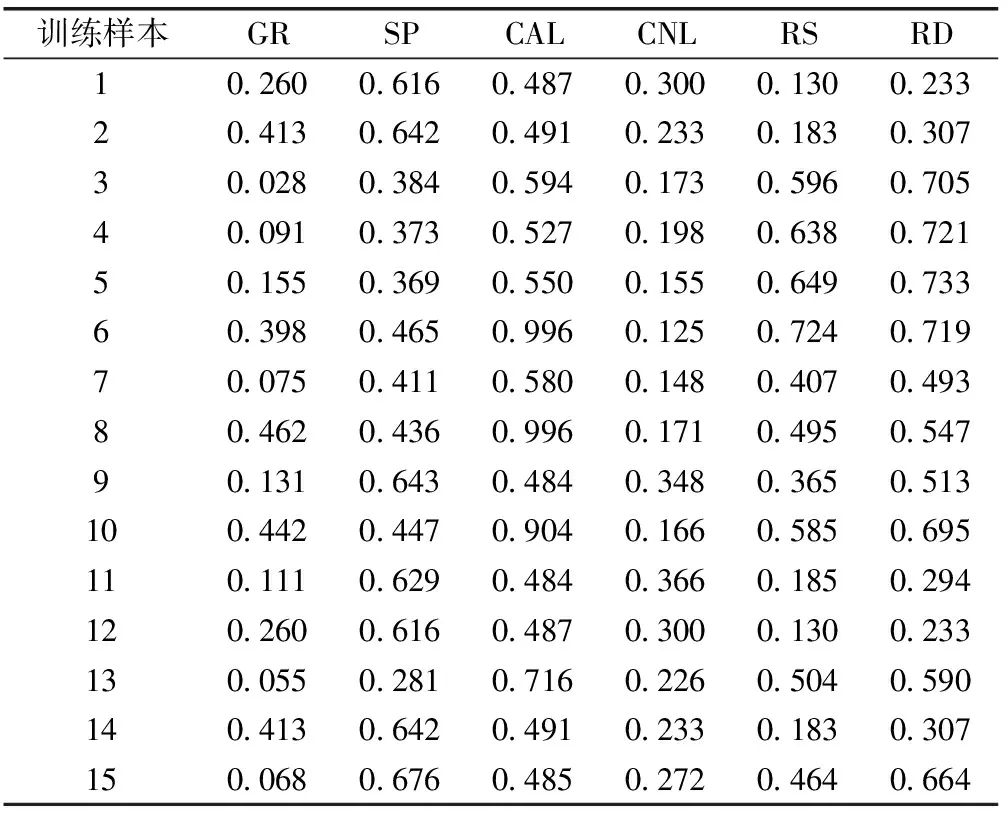
表1 归一化后的部分训练样本

最终聚类结果参数如表2所示，三类中样本个数分别为102、101和105。根据表中聚类中心参数计算得到类间距分别为0.504(第一、第二类间)、0.473(第一、第三类间)、0.509(第二、第三类间)，可以看出类间距离较大，聚类结果符合要求。

表2 K-means算法最终聚类中心

2.2 建立BP神经网络模型

如表2所示，将原始样本聚为三类，且由于类内样本相似度高，部分样本已经具备了该类的全部属性特征，因此分别从每类中按照一定比例抽取样本构建模型，在保留了所有样本特征的情况下提高了模型计算效率。

为了克服BP神经网络算法容易陷入局部最优值、收敛速度过慢等缺陷，采用附加动量法来修正其传递权值和误差阈值。该方法作用于误差反向传递过程，在权值和阈值发生改变前，加上一个动量项，该动量项正比于前次变化量的值，有效减小训练过程中权值和阈值的振荡趋势，加快收敛速度从而找到模型最优解[22]。

基于MATLAB编程，模型采用3 层结构，即1 个输入层、1 个隐含层和1 个输出层：输入层节点数为6 个，分别为归一化后6 个测井参数值；根据经验一般隐含层节点数为输入层的1.5 ～ 2.5 倍，经测试最终确定为12 个；输出层仅1 个节点，即归一化后的裂缝密度，三类模型的训练样本数分别为34、34和35，其他参数如表3所示。

表3 BP神经网络模型参数

图4为3个模型结果的线性回归图，横坐标为样本目标输出值，纵坐标为实际输出值，两者之间明显正相关，线性拟合曲线(实线)与理想曲线(虚线)偏差较小，且相关系数较大，分别为0.95、0.85、0.89，说明模型误差较小，可以用于后续裂缝发育程度识别。

图4 模型训练结果线性回归图

3 裂缝识别与模型验证

同样以塔河油田A探井测井数据作为测试样本进行裂缝发育程度识别。首先利用基于样本间相似度的最短距离算法，将归一化后的测试样本分别划分到某一类中，然后利用对应类的神经网络模型进行预测。设共有I个测试样本，每个样本含N个参数，则第i个样本点坐标为(i1,i2,…,iN)，聚类数为K，第k类的聚类中心坐标为(k1,k2,…,kN)，分别计算第i个样本到第k个聚类中心的距离为Lik[式(1)]，当取到最小值Li时[式(2)]，则代表样本与该类相似度最高，故将其划为该类。

(1)

Li=min(Li1,Li2,…,LiK)

(2)

利用式(1)、式(2)，将103 个测试样本划分到三类中，得到各类样本数分别为34、23、46。分别利用对应的神经网络模型进行预测，并将模型预测结果与目标值进行对比。如图5所示，将三个模型的预测结果作线性回归分析，预测结果与目标值呈明显正相关，回归直线方程斜率分别为0.82、0.76、0.46，相关系数R分别为0.84、0.89、0.76。虽然由于个别样本严重偏离导致R变小，但均达到了0.75以上。表4为部分测试样本预测结果。从表4可以看出，裂缝密度实际值与预测值差异不大，表明模型预测结果较准确。

表4 部分测试样本裂缝密度预测结果

图5 模型预测结果线性回归

为了进一步验证本文方法的有效性，将未考虑样本优化的神经网络模型法与本文方法进行对比，模型设置参数和初始样本保持一致。图6为未考虑样本优化的模型结果。两种方法的模型训练结果如图6(a)、图4所示。由图6(a)、图4可以看出,相关系数R均较大，表明建立的神经网络模型有效；图6(b)与图5为模型预测结果，对比发现本文方法的预测结果(R=0.84、0.89、0.76)明显优于未考虑样本优化结果(R=0.58)。

图6 未进行样本优化的神经网络模型线性回归图

将上述两种方法的预测结果反归一化后与实际裂缝密度值进行对比(图7)，从整体上看本文方法预测的裂缝密度曲线与实际情况更加吻合。在裂缝发育程度低的储层段(图7中Ⅰ段)，该段上部两种方法的预测结果均较好，但在下部本文方法更接近实际情况。在裂缝发育程度较高的储层段(图7中Ⅱ段)，两者的预测结果均显示该段为裂缝极发育段，但本文方法结果和曲线变化趋势与实际情况完全一致。综上，有效验证了本文方法在识别储层裂缝发育程度方面的优越性。

图7 预测裂缝密度曲线对比

4 结论

(1)碳酸盐岩储层埋深大、储集空间复杂多变，储层物性非均质性强，储层裂缝识别和预测十分困难。基于样本优化的BP神经网络方法有效地建立了储层测井参数和裂缝发育程度之间的非线性关系，可以很好地应用于碳酸盐岩储层裂缝发育程度预测。

(2)通过对声波时差AC、自然伽马GR、自然电位SP、补偿中子CAL、井径CNL、浅侧向电阻率(RS)、深侧向电阻率(RD)和密度(DEN)8种常规测井参数与储层裂缝密度参数进行线性回归分析，剔除了声波时差和密度测井这两个相关性较差的参数用于神经网络模型输入，有效提高了裂缝密度识别准确率。

(3)创新性地引入K-means聚类算法优化训练样本，按照相似度准则将308 个训练样本划分为三类，并根据聚类结果在各类中选取代表性样本，分别建立神经网络模型。模型由笼统变得精准、细致，且计算效率显著提高。在模型预测阶段，同样基于相似度的最短距离算法将103 个样本归类，并选择相应的模型进行裂缝密度预测。

(4)采用相同参数设置，验证了本文方法预测碳酸盐岩储层裂缝发育程度效果(R=0.84、0.89、0.76)明显好于未考虑样本优化的结果(R=0.58)。与前人未考虑样本优化的方法相比，本文方法在计算复杂度无明显增加的情况下，识别准确度明显提高，在裂缝发育程度高和裂缝发育程度低的储层段均取得了较好的应用效果，可以作为一种新的非常规碳酸盐岩储层裂缝识别方法，为储层评价和勘探开发提供理论依据。