型钢高性能纤维混凝土粘结滑移性能试验研究
明 铭,郑山锁,2,郑 淏,贺金川,董立国,宋明辰
(1. 西安建筑科技大学土木工程学院,陕西,西安 710055;2. 西安建筑科技大学结构工程与抗震教育部重点实验室,陕西,西安 710055;3. 西安建筑科技大学建筑设计研究院,陕西,西安 710055 )
型钢混凝土组合结构因承载力高、刚度大、抗震性能优异等优点已被广泛应用。良好的粘结性能是保证两种不同性质的材料协调工作的基础[1 − 4]。既有研究表明,因型钢表面较光滑,与混凝土的粘结力较小[5 − 6],在荷载作用下材料的界面间易发生相对滑移,制约了型钢高延性和混凝土高抗压强度能力的充分发挥,进而影响结构及构件的性能[7 − 8]。鉴于此,为保证型钢与混凝土间的协同工作,研发与型钢界面间粘结性能优异的高延性混凝土是充分发挥型钢混凝土组合结构性能优势的有效途径,对进一步推广型钢混凝土组合结构具有重要意义。
在混凝土中添加不连续的延性纤维能够显著提升混凝土的抗拉、抗剪强度和断裂韧性,改善其脆性特征。工程中常用的聚乙烯醇纤维[9 − 10]、聚丙烯纤维[11]或钢纤维[12 − 16]对混凝土的工作性能影响较大,且难以用于掺有较大粒径粗骨料的混凝土中。纤维素纤维是由高寒地区特殊植物制备的新一代高性能纤维,已有研究结果表明[17 − 20],纤维素纤维具有高强高弹性模量、良好的亲水性和体积分散性,将这种短切纤维添加到混凝土中,可以在不影响粗骨料使用的前提下,改善因混凝土强度增加而脆性明显等问题。
型钢与混凝土界面间的粘结性能与混凝土材料的密实性相关。已有研究表明[21],将硅灰等活性矿物掺合料添加到混凝土中,能显著提高混凝土材料的致密性,进而增强型钢与混凝土的粘结性能。但现阶段硅灰产量小、价格高的问题导致其难以满足工程的大量需求。国外学者首先对稻壳展开了较系统的研究,结果表明,稻壳在适当条件下经焚烧、研磨制成的稻壳灰中含有90%~96%的SiO2,化学组分跟硅灰极为接近,能够在一定程度上取代硅灰[22 − 23]。
在混凝土中掺加纤维素纤维和稻壳灰,可制备出具有高强度、高工作性及高韧性的高性能纤维混凝土。将高性能纤维混凝土用于型钢混凝土组合结构中,首先需要对型钢与高性能纤维混凝土间的粘结性能进行深入研究。课题组经过前期的研究对材料配合比进行优化设计,制备出高性能纤维混凝土[24]。本文以不同强度的高性能纤维混凝土、型钢保护层厚度以及型钢锚固长度为变化参数,设计并制作了10 个型钢高性能纤维混凝土试件,采用推出试验方法,对型钢与高性能纤维混凝土之间粘结滑移性能进行揭示。
1 试验概况
1.1 试件设计
试验共设计了10 个型钢高性能纤维混凝土推出试件,截面特征见图1。型钢采用普通热轧工字钢I10,纵筋采用直径14 mm 的HRB335 级钢,箍筋采用直径6 mm 的HPB300 级钢;高性能纤维混凝土设计强度分别为C40、C50、C60、C70,水泥采用秦岭P.O 42.5 普通硅酸盐水泥,细骨料采用中粗河沙,粗骨料采用粒径为5 mm~20 mm均匀级配碎石,聚羧酸系高效减水剂按1.0%~1.5%水泥质量比例掺入城市自来水,各材料组分见表1。本试验采用的稻壳灰系安徽省某保温材料厂生产,SiO2质量分数为91.2%,烧失量为3.90%,其化学组分与硅灰接近;纤维采用上海罗洋新材料科技有限公司从美国Buckeye 公司引进的UF500纤维素纤维,其物理力学性能见表2。各强度等级的高性能纤维混凝土试件均预留了6 个标准立方体试块,钢材及高性能纤维混凝土力学性能指标见表3。试件设计参数见表4。

图1 试件截面尺寸 /mm Fig.1 Section of specimens
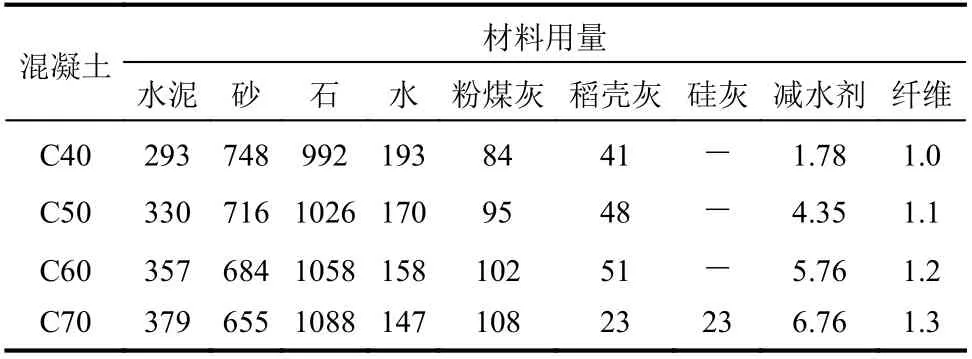
表1 高性能纤维混凝土配合比 /(kg/m3)Table1 High performance fiber reinforced concrete proportions

表2 纤维素纤维物理力学性能Table2 Mechanical properties of cellulose fiber

表3 钢材、高性能纤维混凝土材料性能Table3 Material properties of steel and high performance fiber reinforced concrete
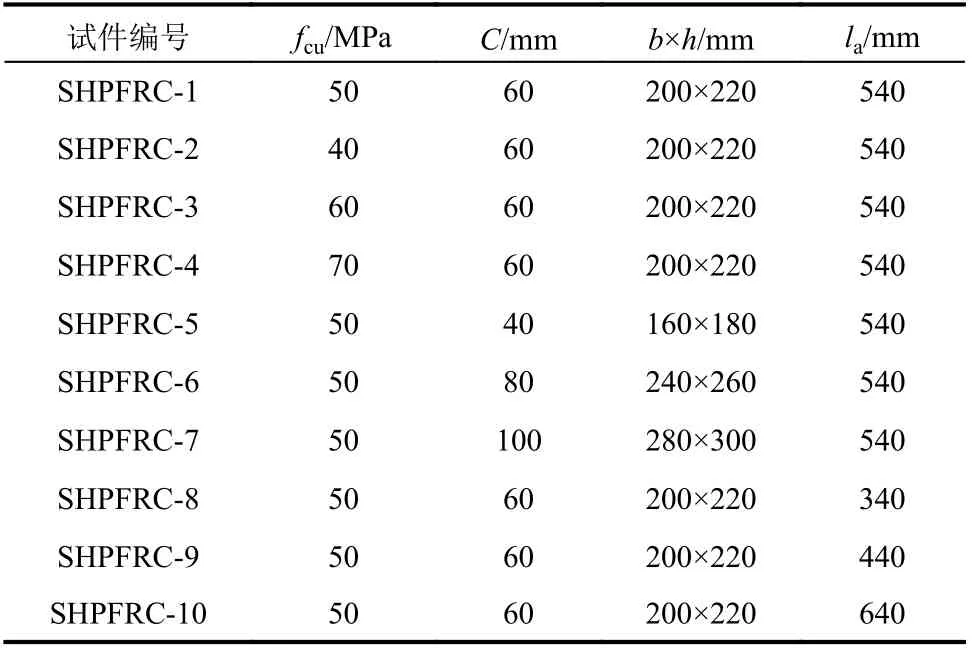
表4 试件设计参数Table4 Design parameters of specimens
1.2 量测方案
通过在加载端和自由端布置位移计量测型钢与高性能纤维混凝土之间的相对滑移量。加载端的相对滑移由布置在型钢与高性能纤维混凝土上位移计的差值得到。自由端的相对滑移借助于焊接在型钢自由端的钢棒实现,位移计底座固定在特制钢垫板上,钢垫板使得自由端混凝土固定不动,指针垂直打在粘贴在钢棒上的小木条上,型钢从钢垫板的“工”字形缝中推出,推出的距离即为自由端型钢与高性能纤维混凝土之间的相对滑移,详见图2(b)。
1.3 加载方案
试件推出试验的加载装置如图2 所示,加载速率为0.3 mm/min,加载端型钢和自由端混凝土在试验前打磨平整后,荷载直接作用在加载端型钢上,自由端混凝土通过30 mm 厚的特制钢垫板与试验台座相连。当自由端的相对滑移量达到6 mm,或试件表面裂缝不再发展,荷载下降速率基本不变时,停止加载。

图2 试验加载装置Fig.2 Test loading devices
2 试验结果与分析
2.1 试件破坏形态
加载初期,加载端和自由端均无滑移产生。荷载增至极限荷载的30%~50%时,加载端开始滑移,试件表面未出现裂缝。荷载增至极限荷载的80%左右时,加载端滑移逐渐发展,且附近混凝土表面出现裂缝,部分试件自由端滑移,但滑移量较小,发展较慢。荷载增至极限荷载时,伴随着一阵劈裂声,裂缝由加载端附近向上迅速发展,并形成许多细小分支裂缝,同时加载端面裂缝由型钢翼缘肢尖和中部向外延伸至混凝土侧表面。
由于试件设计参数的变化,试件的裂缝形态表现出一定差异:保护层厚度(SHPFRC-5)、锚固长度(SHPFRC-8)较小试件的荷载出现了陡降,裂缝在浇筑面产生并迅速贯通试件全截面,表现出较大的脆性;保护层厚度较大(SHPFRC-6、SHPFRC-7)的试件四个侧面均有裂缝产生,由加载端角部向上发展,裂缝发展到约1/3 型钢锚固长度时停止发展,宽度自加载端向上逐渐减小,试件呈瓜梨形破坏。部分试件破坏形态见图3,可见随着保护层厚度和锚固长度的增加,各试件裂缝的宽度增加,长度有所减小。随着荷载下降速率平缓,裂缝停止发展,型钢与混凝土之间的相对滑移趋于稳定。自由端面基本无裂缝产生,推出的型钢表面较光滑,并伴随混凝土磨削。
2.2 荷载-滑移曲线

图3 部分试件破坏形态图Fig.3 Failure modes of specimens
各试件的荷载-滑移曲线(P-S 曲线)如图4 所示。可以看出,各试件的P-S 曲线呈现出一定的规律性,归纳出的典型曲线如图5(a)和图5(b)所示。加载端P-S 曲线呈现直线上升段(OA)、荷载上升段(AB)、荷载下降段(BC)和水平残余段(CD)四个阶段,直线上升段A 点对应荷载为初始滑移荷载P0,P-S 曲线峰值B 点荷载为极限荷载Pu,荷载下降段C 点对应的荷载为残余荷载Pr,各试件特征荷载值见表5;试件自由端P-S 曲线与加载端的下降段曲线基本一致,荷载达到残余荷载后曲线出现重合,并维持在极限荷载的约50%~70%。
3 特征粘结强度
3.1 特征粘结强度定义及影响因素分析
采用平均粘结应力描述型钢高性能纤维混凝土界面粘结应力在加载过程的分布规律,假定粘结应力沿型钢锚固长度均匀分布,计算公式如下:

图4 荷载-滑移曲线Fig.4 Load-slip curves

图5 典型荷载-滑移分布曲线Fig.5 Classic load-slip curves

表5 试件特征值Table5 Characteristic values of specimens

式中:P/kN 为试验时施加的外荷载;Ca为型钢截面周长,取458.69 mm; la/mm 为型钢与高性能纤维混凝土的锚固长度。采用平均粘结应力分析各设计参数对型钢高性能纤维混凝土界面滑移的影响规律,各试件粘结强度特征值计算结果见表5,其中,初始粘结强度τ0、极限粘结强度τu、残余粘结强度τr分别为对应于P0、Pu、Pr的粘结应力。
1)高性能纤维混凝土强度
图6 给出了特征粘结强度与高性能纤维混凝土劈裂抗拉强度的相关关系。可以看出,随着混凝土强度的提高,特征粘结强度均呈增加趋势,其中极限粘结强度增长速率最为显著。这是因为:在型钢与高性能纤维混凝土的粘结力组成中,化学胶结力是主要的组成成分,化学胶结力的大小取决于混凝土材料组分和抗拉强度的大小,因而可通过提高混凝土的抗拉强度和抗裂韧性来提高型钢与混凝土界面过渡层的强度,进而提高型钢与高性能纤维混凝土之间的粘结强度;纤维素纤维具有良好的阻裂增韧性能,能够改善由于混凝土强度提高而脆性更加显著的问题,使得极限粘结强度和残余粘结强度不仅没有因为混凝土强度的提高而降低,反而有所提升。
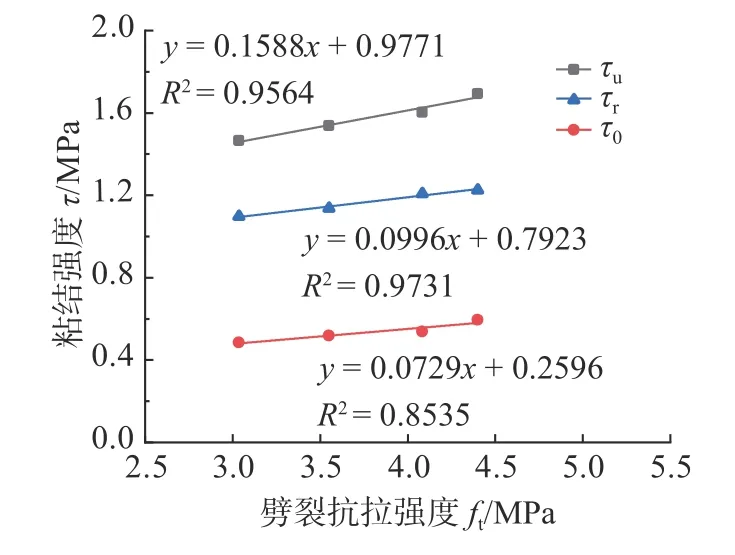
图6 粘结强度与劈裂抗拉强度的相关关系Fig.6 Relationship between bond strength and splitting tensile strength
2)保护层厚度
图7 为各特征粘结强度与相对保护层厚度(保护层厚度Ca与型钢截面高度ha之比)之间的相关关系。可以看出,粘结强度特征值均随型钢相对保护层厚度的增大呈增大趋势,其中在保护层厚度较大时初始粘结强度的增长速率略高于其他特征粘结强度。这是因为,在一定范围内,混凝土对型钢的约束能力随保护层厚度的增大而增大,进而粘结界面上的正应力及相应的摩擦阻力越大;初始粘结强度主要以化学胶结力的形式存在,而极限粘结强度和残余粘结强度则主要以摩擦阻力和机械咬合力的形式存在,在滑移阶段,保护层厚度的增加对机械咬合力和摩擦阻力的提高作用会逐渐减弱。

图7 粘结强度与相对保护层厚度的相关关系Fig.7 Relationship between bond strength and relative thickness of concrete cover
3)锚固长度
各特征粘结强度与相对锚固长度(锚固长度la与型钢截面高度ha之比)之间的相关关系如图8所示。可以发现,特征粘结强度均随锚固长度的增加呈下降趋势。其中,极限粘结强度的下降速率最为显著,这是由于随着锚固长度的增加,粘结应力扩散长度上高应力区相对分布长度逐渐变小;初始粘结强度由于型钢与高性能纤维混凝土界面主要以化学胶结力的形式存在,而化学胶结力在试件产生滑移前,只在加载端附近存在,随着锚固长度的增加,远离加载端无粘结力部分的长度增加,则按沿型钢全锚固长度上计算的初始粘结强度降低;残余粘结力是在型钢高性能纤维混凝土全截面产生滑移后,主要以摩擦阻力和机械咬合力的形式存在,受锚固长度的影响较小。
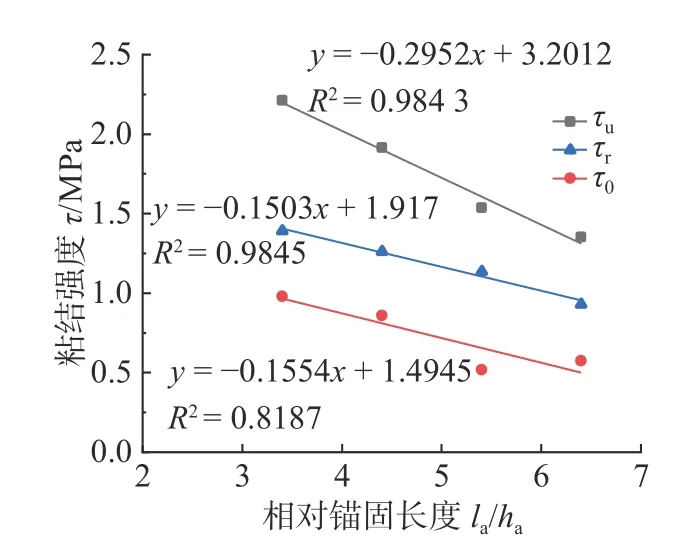
图8 粘结强度与相对锚固长度的相关关系Fig.8 Relationship between bond strength and relative embedded length
3.2 特征粘结强度计算公式和验证
图6~图8 为各特征粘结强度与高性能纤维混凝土强度、型钢相对保护层厚度和相对锚固长度的散点图及拟合结果。可以看出,各特征粘结强度受不同影响因素的变化规律不尽相同,但均呈线性变化趋势。结合试验结果,对各特征粘结强度与高性能纤维混凝土劈裂抗拉强度、型钢相对保护层厚度以及相对锚固长度进行多元线性回归,在进行多元线性回归时,不同影响因素的试验结果均预留一个试件,对回归结果进行验证,建立各特征粘结强度的计算公式如下:
初始粘结强度:

极限粘结强度:
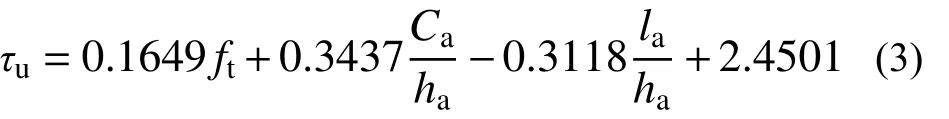
残余粘结强度:

式中:ft/MPa 为高性能纤维混凝土的抗拉强度;Ca/mm 为型钢的保护层厚度;ha/mm 为型钢的截面高度;la/mm 为型钢的锚固长度。
表6 为预留试件特征粘结强度计算值与试验值的对比结果,可以看出,初始粘结应力、极限粘结应力和残余粘结应力的试验值与计算值比值的平均值分别为0.893、0.982、1.027,相应的变异系数分别为0.070、0.007、0.008。因此,基于混凝土强度、保护层厚度以及锚固长度这四种因素统计回归出的公式,能够满足型钢与高性能纤维混凝土之间特征粘结强度的计算要求。
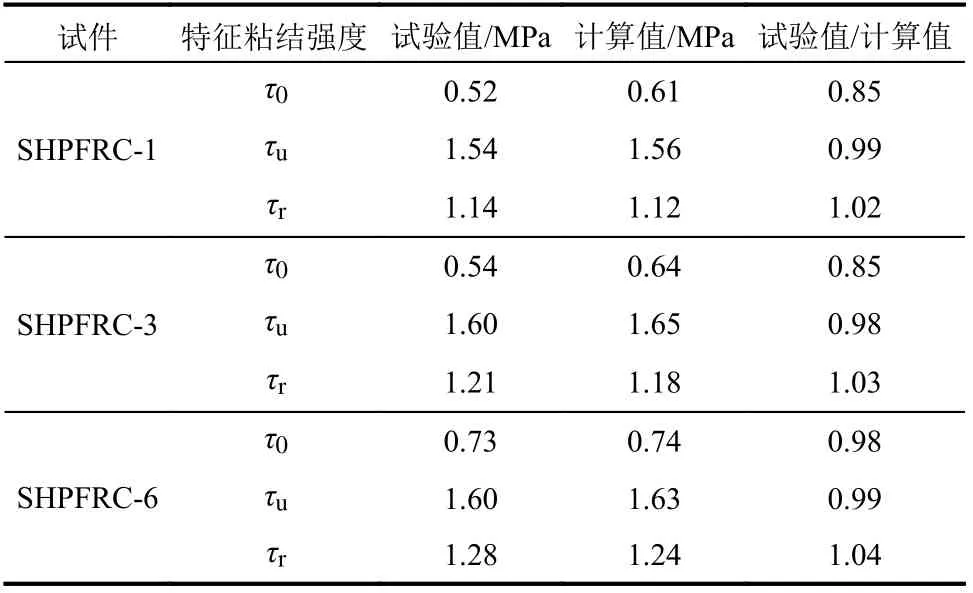
表6 特征粘结强度的试验值与计算值对比Table6 Comparison measured characteristic bond strength with calculated strength
4 有效粘结应力推导与分析
4.1 有效粘结应力的定义与推导
在外荷载加载过程中,粘结应力并不始终存在于型钢与高性能纤维混凝土界面。粘结应力产生于试件加载端,随着外荷载的增加逐渐向自由端扩散,并最终贯穿于型钢全锚固长度,而不同加载时期,化学胶结力、机械咬合力和摩擦阻力在粘结应力中所占比重不同。平均粘结应力是沿型钢全锚固长度上粘结应力的平均值,不能表达粘结应力各组成部分的发展变化过程。为精确反应粘结应力的发展变化过程,在荷载发展阶段,型钢与高性能纤维混凝土界面上粘结力作用段的长度用有效锚固长度ln表示,ln范围内界面层的粘结应力的平均值称为有效粘结应力 τ′,如式(5)所示。

式中:Ca为型钢的截面周长,取458 mm;P/kN 为外荷载;ln/mm 为有效锚固长度,由固定粘结扩散长度l0和滑移段长度lx组成,固定粘结扩散长度是有效锚固长度上存在化学胶结力的范围,位于滑移段和无粘结应力段间,文献[7]取固定粘结扩散长度近似为型钢的横截面高度。
对图5(a)试件加载端典型荷载-滑移曲线荷载上升段(AB 段)的有效粘结应力进行推导。当加载端型钢与高性能纤维混凝土产生相对滑移,化学胶结力将丧失,此时对应的初始滑移荷载为P0,滑移段上相应地产生摩擦阻力和机械咬合力,同时,在与滑移段相邻的未滑移段上产生了量值为P0的化学胶结力,存在化学胶结力的长度为固定粘结扩散长度l0。荷载增至Pu的过程中,固定粘结扩散长度由加载端转移至自由端,且化学胶结力始终存在于固定粘结扩散长度范围内。故假定固定粘结扩散长度l0和滑移段长度lx上的粘结应力为均匀分布,分别取 τ0和 τx。
图9(a)~图9(c)分别为试件加载端典型荷载-滑移曲线上初始滑移点A、极限荷载点B、A 与B 点间任一点E 的粘结应力分布图。在初始滑移点A,加载端形成固定粘结扩散长度,化学胶结力达到最大值,并承担全部外荷载,此时粘结应力平衡方程可表示为式(6);在极限荷载点B,固定粘结扩散长度发展到试件的自由端,外荷载由未发生滑移段上的化学胶结力以及滑移段上的摩擦阻力和机械咬合力共同承担,有效粘结长度等于型钢锚固长度,该点粘结应力平衡方程如式(7)所示;在E 点处有效锚固长度介于固定粘结扩散长度和型钢锚固长度之间,粘结应力平衡方程见式(8)。
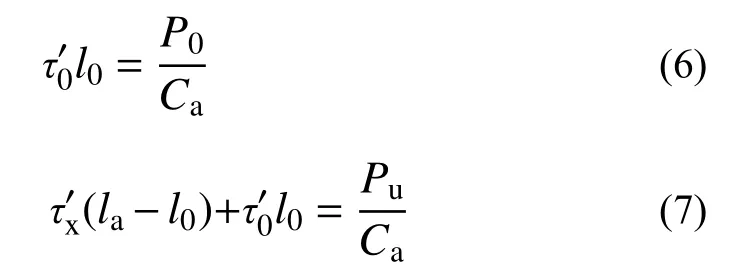
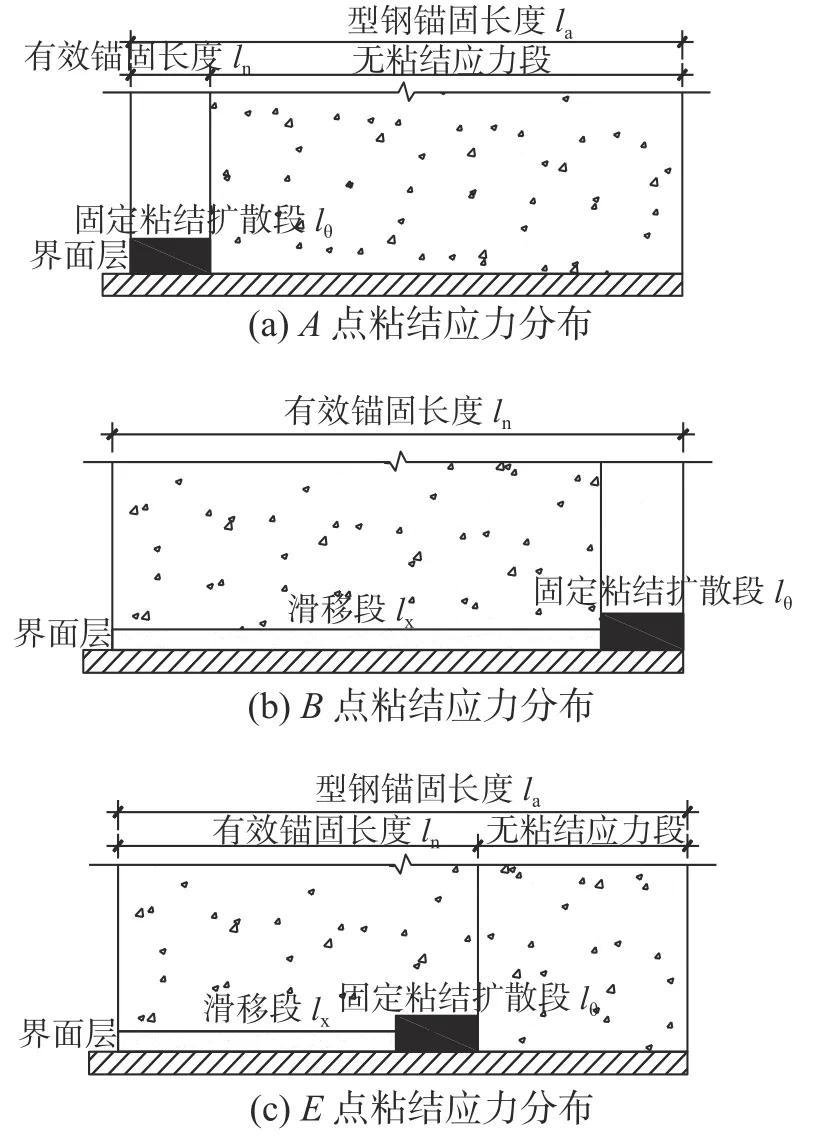
图9 粘结应力分布图Fig.9 Schematic plot of bond force distribution

结合式(6)~式(8)可得:
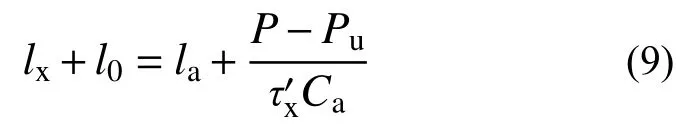
则有效锚固长度为:
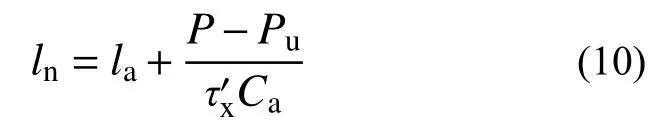

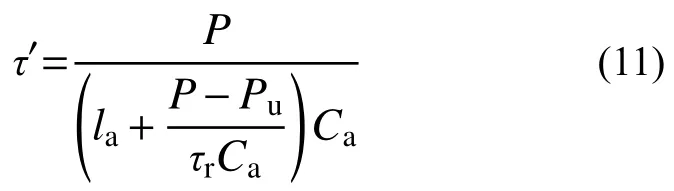
式中, τu为有效粘结应力。在荷载上升段,荷载由P0增至Pu的过程中,有效粘结应力随残余粘结应力和极限荷载的增大而增大,与型钢锚固长度成负相关,故提高混凝土对型钢的约束作用可有效提高型钢与混凝土间的粘结应力。而高性能纤维混凝土由于加入纤维素纤维,其阻裂与增韧性能得到的较大改善,对型钢的整体约束能力增强,能显著提高粘结力。当荷载大于极限荷载Pu时,型钢的有效锚固长度为la,此时的有效粘结应力按式(1)计算。
4.2 有效粘结应力-滑移曲线全过程分析
各试件有效粘结应力-滑移曲线见图10,根据各试件τ′−S曲线呈现出的规律性,归纳得到典型曲线见图11。可以看出,典型曲线可分为无粘结滑移段(OA 段)、曲线下降段(AB 段)、陡降段(BC段)、水平残余段(CD 段),各阶段发展过程如下:


图10 有效粘结应力-滑移曲线Fig.10 Effective bond strength-slip curves

图11 典型的有效粘结应力-滑移曲线Fig.11 Classic effective bond strength-slip curve
曲线下降段(AB 段):试件加载端产生滑移后,滑移段中的化学胶结力随即消失,并逐渐向自由端扩展;同时滑移段界面上微小厚度的混凝土被剪断或压碎使得体积增大,在箍筋的横向约束下产生了正应力,进而产生摩擦阻力和机械咬合力。在与滑移段相邻的固定粘结扩散长度l0上产生了量值为P0的化学胶结力,此阶段外荷载由固定粘结扩散长度l0的化学胶结力和滑移段lx的摩擦阻力及机械咬合力共同提供。随着滑移段的扩展,摩擦阻力和机械咬合力的总和增大,有效锚固长度增加,而有效粘结强度不断降低,这说明化学胶结力的值远远大于摩擦组合和机械咬合力的总和。当l0发展到自由端时,有效锚固长度等于型钢锚固长度la,此时的有效粘结应力与极限粘结应力τu相等,对应于τ′−S曲线上的B 点。
陡降段(BC 段):固定粘结扩散长度扩散到试件的自由端时,有效锚固长度等于型钢锚固长度。滑移段继续向自由端扩展,化学胶结力逐渐在自由端丧失,摩擦阻力和机械咬合力的增量远小于化学胶结力的降低量,有效粘结应力-滑移曲线出现了陡降。当滑移段贯穿型钢锚固长度,化学胶结力全部消失,此时对应的有效粘结应力仅由摩擦阻力和机械咬合力组成。
水平残余段(CD 段):滑移扩展至全锚固长度后,界面层微小混凝土被全面压碎,当破损混凝土颗粒累积到一定程度,界面间压应力使得混凝土内产生拉应力而开裂。相对滑移继续发展,混凝土内裂缝达到稳定,其界面上破损混凝土颗粒被整合,机械咬合力逐渐减小,当有效粘结应力τ′稳定不变时,可认为破损混凝土颗粒整合完成同时机械咬合力消失,此时有效粘结应力即为摩擦阻力,大小为水平残余段终点D 点对应的粘结应力 τr2。
通过对有效粘结应力-滑移曲线全过程分析可知,当加载端产生滑移时,型钢与高性能纤维混凝土之间的化学胶结力达到最大值,故化学胶结力可用加载端开始产生滑移时的初始粘结应力τ0表示;水平残余段起点处粘结应力由摩擦阻力和机械咬合力提供,当有效粘结应力趋于稳定时,可认为界面层破损混凝土颗粒已被整合,进而机械咬合力丧失,故摩擦阻力可由水平残余段终点对应的粘结应力 τr2代替;机械咬合力由水平残余段起始点粘结应力 τr1和终点粘结应力 τr2的差值表示。
通过对各试件的分析,得到试件HPFRC-1~HPFRC-10 的有效粘结应力各特征点的实测结果如表7 所示,由表可知,化学胶结力、摩擦阻力和机械咬合力三者比值的平均值为1∶0.234∶0.073,摩擦阻力和机械咬合力相对于化学胶结力的变异系数分别为0.089、0.047,离散性较小。由此可见,在粘结应力的各组成组分中,化学胶结力最大,摩擦阻力次之,机械咬合力最小;并且摩擦阻力和机械咬合力之和约占化学胶结力的1/3,机械咬合力约占摩擦阻力的1/3。

表7 粘结应力组份Table7 Proportion of bond strength components
5 结论
本文通过10 个推出试件的试验与理论分析,对型钢高性能纤维混凝土粘结滑移性能的主要问题进行了研究。得到以下主要结论:
(1) 通过型钢高性能纤维混凝土粘结性能推出试验得到各试件荷载-滑移曲线,试件加载端荷载-滑移曲线呈直线上升段、荷载上升段、荷载下降段和水平残余段四个部分,荷载上升段、荷载下降段、水平残余段起点分别对应初始荷载、极限荷载及残余荷载;试件自由端荷载-滑移曲线规律与加载端曲线的下降段基本一致,荷载达到残余荷载后二者出现重合,并维持在极限荷载的50%~70%。
(2) 特征粘结强度受不同设计参数影响的变化规律不尽相同,但基本呈线性变化趋势。增加混凝土强度和型钢保护层厚度,能有效提高型钢与高性能纤维混凝土间的粘结强度;而随着锚固长度增加,特征粘结强度均呈下降趋势。根据试验结果,建立特征粘结强度计算公式,初始粘结强度、极限粘结强度与残余粘结强度试验值与计算值比值的均值分别为0.893、0.987、1.030,表明计算值与试验值吻合较好。
(3) 分析试件加载端荷载-滑移曲线各点粘结应力分布,引入有效粘结应力,其计算公式能够反应粘结应力的发展变化过程;有效粘结应力与型钢的锚固长度、极限荷载值和残余粘结强度有关,残余粘结强度和极限荷载成正比,与型钢的锚固长度成反比。
(4) 对有效粘结应力-滑移曲线全过程进行分析,得到粘结应力各组成部分的计算方法,化学胶结力、摩擦阻力和机械咬合力三者比值的平均值为1∶0.234∶0.073。

