基于改进BPR模型的封闭小区开放对城市道路通行能力影响研究

田 飞，王锦升

(1.海南经贸职业技术学院 科研处，海南 海口 571127；2.海口经济学院 科学计算与应用数学实验室，海南 海口 571127)

2016年2月21日，国务院发布《关于进一步加强城市规划建设管理工作的若干意见》[1]，其中第十六条关于推广街区制，原则上不再建设封闭住宅小区，已建成的住宅小区和单位大院要逐步开放等意见，引起了广泛地关注和讨论.除了开放小区可能引发的安保等问题外[2]，议论的焦点之一是：开放小区能否达到优化路网结构、提高道路通行能力、改善交通状况的目的[3]，以及改善效果如何.

1 封闭小区开放对周边道路通行能力影响的评价指标体系

影响封闭小区开放对道路通行能力的4个大指标[4]为城市结构与交通结构、道路基础设施、道路规范管理和道路服务能力[5]，15个初选小指标为：非直线系数、路径数量、道路宽度、道路面积、路口数量、小区出口数量、出行时间、人流量、基础设施面积、非机动车数量、绿化面积、交通事故数量、停车位面积、交通信号系统覆盖率、交叉路口阻塞率和通行车辆等.

通过海南省交通运输厅网站获取以上15个初选指标2016～2019年的数据，代入到BP神经网络模型，运用SPSS软件做KMO检验，得到KMO的值为0.850，根据Kaiser给出了常用的KMO度量标准[6],KMO的值大于0.8，表示各变量之间不独立，适合做因子分析.

将数据代入SPSS软件,根据提取特征值的条件——特征值大于1，结合国际《道路通行能力手册》[7]服务水平划分和《城市交通管理评价指标体系》中交通拥挤程度评价表，筛选出影响小区开放对周边道路通行的指标为路径数量、道路基础设施的面积、非直线系数和交叉路口阻塞率等4个指标，如图1所示.

图1 指标贡献折线对比图

2 基于改进BPR模型的封闭小区开放前后对道路通行的影响

建立改进BPR模型[8]以达到最优化.优化函数为：

F:x→R+,x∈S,

(1)

它表示优化问题的一个可行解，R+={y|y∈R,y>0}，S表示函数的定义域.N(x)⊆S表示x的一个邻域集合.首先给定一个初始T0和该优化问题的一个初始解X0，并由X0成下一个解x′∈N(x(0))，是否接受x′作为一个新解x(1)依赖于下面概率：

(2)

如果生成的解x′的函数值比前一个解的函数值更小，x(l)=x′作为一个新解.否则以概率p(x(0)→x′)接受作为x′一个新解.

当自行车交通量没有超过通行能力时干扰系数取0.8，超过通行能力时干扰系数为：

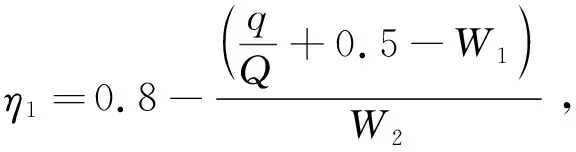
(3)

其中：η1为自行车对机动车干扰系数；Q为非机动车道路每米自行车设计通行能力；q为道路上实测到的自行车交通量；W1为单向非机动车宽度；W2为单项机动车宽度.

综上得到改进后的BPR综合阻抗函数为：

(4)

(5)

其中：TD为路段ij上行走的时间；tij为在第i个路段上的自由流时行走的时间；x为车道饱和度；N为从i到j所经过的红绿灯个数；T为红绿灯周期长度；Vij为当时的交通流量；T′为路段上行走的时间；tq为绿灯时间长.

由上面公式可知，当车辆的数量一定时.开放小区后，周边道路通行主要发生变化[9]的是：主干道车流量减少，主干道上的延误时间减少，自由行驶的时间变长，从而可以大大提高主干道的通车能力，缓解主干道的通车压力.另外，一部分车从小区通行，可能会由于小区构造不同，路段不同，在主干道车辆较少时，会造成经过小区到达B地的车辆比从主干道直接到B地的车辆花费更多的时间.但是，当主干道的通车数量达到一定时，会大大提高通车效率.

3 实证仿真与分析

以海口市某6个小区为例[10]，其中2、3、6小区周围交通流量较大，2、3、4小区结构影响较大，3、5，6小区非直线系数较大.其中有1、3这两个小区，属于周边车流量差别较大型，2、4这两个小区属于小区结构差别较大型.还有5、6这两个小区属于非直线系数差别较大型.

2019年9月至12月份，通过与交通管理部门协作和6个小区实地试验，获取研究所需各种数据，分别计算出小区开放前后经主干道到达时间及经过小区到达的时间[11]，见表1.

表1 小区开放前后到达时间表

通过上表中的行车时间，根据BPR改进的模型计算出[12]一天24 h内，不同小区构造，不同周围的道路结构，不同车流量的相对车辆通车数.这些小区的相对通车数量如图2所示.

图2 6小区开放前后车辆对比图

不难发现，无论是哪种结构的小区，只要小区开放，单位时间内主干道上通过的相对车辆的数量相比以前没开放时都多.表明开放小区后的车辆行驶压力更小了，缓解了道路交通压力.开放前与开放后车辆的相对通车数量相差越大，就说明开放小区后产生的效果越明显.

对比小区1与小区3，差别最大的是周围道路流量，小区1周围的通车流量较小，小区3周围的车流量较大，其它因素相差不大.小区开放后，通过图3可知，两个小区周围主干道相对通车数量增加了，说明主干道更流畅了，进一步说明小区开放缓解了周围道路的行车压力.但是主干道相对通车数量增加幅度都不大，所以周围的主干道车流量在小区开放后对缓解主干道交通压力的效果不是很明显.

图3 小区1、3开放前后车辆对比图

对比小区2与小区4.这两个小区的结构差别最大，即小区路的道路宽度、人流量和非机动车辆、十字路口数差别很大，而周围的车流量，两地的非直线系数相差不大.通过柱形图4的对比，当住宅区的结构较好时，小区开放后会有更多的车辆选择小区这条路行驶，相反大部分车辆宁愿从拥挤的主干道过，也不愿意走小区这条路.因此在这小区开放后，小区2比小区4产生的效果更大.总体来说，小区的结构会对小区开放效果产生较大的影响.

图4 小区2、4开放前后车辆对比图

如图5所示，小区5与小区6的主要差别是小区6开放后，主干道的通车相对数量大幅增加，影响效果显著.两个小区其他条件大致一样，但就因为非直线系数的差别，从而导致了小区开放后产生的效果巨大.因此可以得出，非直线系数对于小区开放的效果影响巨大.

图5 小区5、6开放前后车辆对比图

4 结 论

建立了改进的BPR模型，运用Spss和Matlab软件进行了定量分析，研究了城市住宅区的开放对周边道路通行的影响.通过对6个不同小区开放前后比较分析，同一个小区从封闭状态到开放状态后，单位时间内主干道上通过的相对车辆的数量相比没开放时增多，表明了开放小区后的主干道上车辆行驶压力更小，缓解了主干道路上的交通压力.