交通基础设施对全要素生产率的影响研究——基于省际空间面板模型的实证分析

唐松林,商潇婉

(山东工商学院 经济学院,山东 烟台 264025)

一、引言

中国自改革开放以来,国内铁路营运总里程从2000年的6.87万公里提升至2008年的7.97万公里,2017年的12.7万公里。2017年,我国高速铁路营业里程已达2.5万公里,位居世界第一,“四纵四横”高铁网经基本形成。国内公路营运总里程从2000年的167.98万公里提升至2008年的373.02万公里,2017年的477.35万公里。铁路和公路基础设施建设取得了举世瞩目的成就。同时,中国经济也维持了超过30年的高速增长。然而2012年之后,中国GDP年度增长率开始降到8%以下,2015年已经降到7%以下,中国经济能否持续增长,近年来成为经济学者研究的热点问题。学者们普遍认为交通基础设施投资是经济发展的基础,交通基础设施投资与全要素生产率增长之间的关系也一直是经济研究者们重点关注的问题。

对基础设施与经济增长关系的实证研究最早由Aschauer完成[1],后续一些学者Munnell、Merriman、Wylie等基于时间序列数据测算交通基础设施的产出弹性[2-4]。由于多重共线性等问题的存在,估计结果在精度和有效性方面都受到了限制。时间序列样本数据的估计的基础设设施产出弹性较大,许多学者对此提出了质疑。面板数据能够较好的克服时间序列数据你就中存在的多重共线性问题并可以控制不可观测变量对结果的影响。因此部分学者Munne、Nourzad和Vrieze、Kamps等采用面板数据进行研究,改善了时间序列数据分析方面的不足[5-7]。

在国内,关于交通基础设施方面的研究起步比较晚,在理论的创新上也比较少。但是关于实证方法的创新和应用比较多。并取得了不少的研究成果。空间计量是近几年新兴的研究方法,比如,刘秉镰等使用空间面板计量模型对交通基础设施与中国的全要素生产率增长之间的关系,以及交通基础设施的空间溢出效应进行研究[8]。其结果表明交通基础设施水平对全要素生产率增长存在显著的正向影响,且主要是外溢效应引发的增长,来自空间外溢效应的部分则高达74.3%。余泳泽和刘大勇通过空间面板计量方法研究发现企业创新对科技创新的空间外溢效应明显[9]。边志强研究发现外地网络基础设施的完善会造成本地生产要素外流,进而对本地产生负的溢出效应[10]。胡煜、李红昌通过划分交通枢纽等级并分析空间分布情况,研究发现不同地区交通枢纽的空间溢出效应存在明显差异,东部和中部地区各类交通枢纽的空间溢出效应显著为正,中部地区不同交通枢纽间的差异不明显,西部地区只有区域性交通枢纽有显著正的空间溢出效应[11]。边啸通过研究发现铁路基础设施主要通过溢出效应影响全要素生产率的提高,公路基础设施主要通过直接效应提高本地的全要素生产率[12]。汪晓文等利用“一带一路”沿线15个省市区2001-2015年的面板数据研究发现,基础设施投资不会直接促进全要素生产率的提高,不同类型的基础设施存在不同的间接溢出效应,信息、城市基础设施促进全要素生产率的提高,但交通、能源基础设施的促进作用并不显著[13]。谢剑利用地级市面板数据,构建了空间动态杜宾模型分析经济性基础设施和社会性基础设施对中国各地级市全要素生产率变动的影响[14]。总体上,各地级市的全要素生产率呈下降趋势,交通基础设施会对当地的全要素生产率产生正向影响,但会对邻近区域的全要素生产率产生负向空间溢出效应。施震凯等以首次开通的动车组列车停靠站点作为分组依据,采用倍差分析法研究发现,铁路提速显著提高了途经地区企业的技术进步,对效率改进的影响为正但不显著[15]。梁喜、李思遥认为实现交通基础设施的绿色转型是缓解交通与自然之间矛盾的必然选择[16]。所以选取绿色全要素生产率作为被解释变量,采用空间杜宾模型研究交通基础设施的空间溢出效应。

以上研究成果都是把不同的交通基础设施作为相互独立的整体来分别考察其对经济增长水平的数量或者质量的影响。虽然在一定程度上很好的解释了交通基础设施对经济增长的内在影响机制,但是并没有考虑到不同交通基础设施之间的联合影响效应。因此,本文在考虑不同交通基础设施独立影响的同时,也会考虑不同交通基础设施之间的联合影响机制。

二、交通基础设施对全要素生产率的影响机理分析

交通运输是资源和人才流动的重要载体,是经济发展的重要依托。其对经济的影响可分为直接和间接两部分。直接影响是对经济的直接拉动作用,是指交通基础设施的建设、运营等不仅能够创造大量就业,同时投资也能够通过乘数效应促进经济的发展。间接影响是指对经济的间接拉动作用。交通运输对区域经济的影响主要体现在交通基础设施建成运营以后对区域经济发展的影响,铁路公路基础设施建成以后,运输速度、运输量都有了极大的改善。对要素流动、资源优化配置、和人们的生活方式都产生了深刻影响。

刘秉镰等认为交通基础设施可在三个方面带动全要素生产率的提高[8]。一是其发展会促进和增加劳动力和商品在区域间的流动,这样产生于空间某一点的新知识和新技术就可以更广泛的传播。区域通达性的提高会降低运输成本,这有利于使落后地区引进先进技术和人才。二是其发展可优化资源配置,实现帕累托改进,使配置状态向最优配置靠近。三是其发展有利于经济集聚和市场扩张,从而为规模效率的提高提供空间。

交通基础设施的网络性,使得分散的各区域连成一个整体,但并不是所有区域都能够因此获益。可达性的改变,使得经济发达的地区既可能通过扩散效应促进邻近区域的发展,产生正向空间溢出效应。也可能会由于其强大的吸引力产生“虹吸效应”,从而使落后地区的生产要素、劳动力等资源流向这些发达地区,反而抑制这些落后地区的生产率,从而产生负的溢出效应。

三、交通基础设施对全要素生产率的实证分析

本文使用stata15对2000-2017年我国交通基础设施和全要素生产率之间的关系进行估计。

(一)空间权重矩阵的定义及设定

常见的空间权重矩阵主要有0-1邻接矩阵、距离矩阵和经济距离矩阵。为了同时考察各区域间的空间因素与经济发展因素,本文选用经济距离矩阵作为构建空间计量模型的权重矩阵。设W为n阶经济距离矩阵,其定义如式(1)所示:

(1)

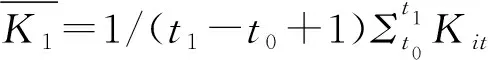
(二)空间相关性检验

空间子相关性分析用于判定被解释变量和主要解释变量的空间特征,这是设定计量模型的前提。一般使用空间自相关指数MoranI来描述空间自相关性。MoranI的取值范围为(-1,1)。MoranI的绝对值越大,所检验的经济变量的空间相关性越强。当其值属于(0,1)时存在空间正相关,即空间集聚;当其值属于(-1,0)时存在空间负相关,即空间排斥;当其等于0时,表明不存在空间相关性。2000-2017年中国各省级地区全要素生产率和铁路密度的全局莫兰指数I检验结果如表1所示,它考察的是整个空间序列的空间集聚情况。2000-2017年各个年份中的Moran I 值均为正值且通过了 1% 水平下的显著性检验,说明该时段我国省级地区的全要素生产率和铁路密度在空间上的确存在着明显的正自相关关系。

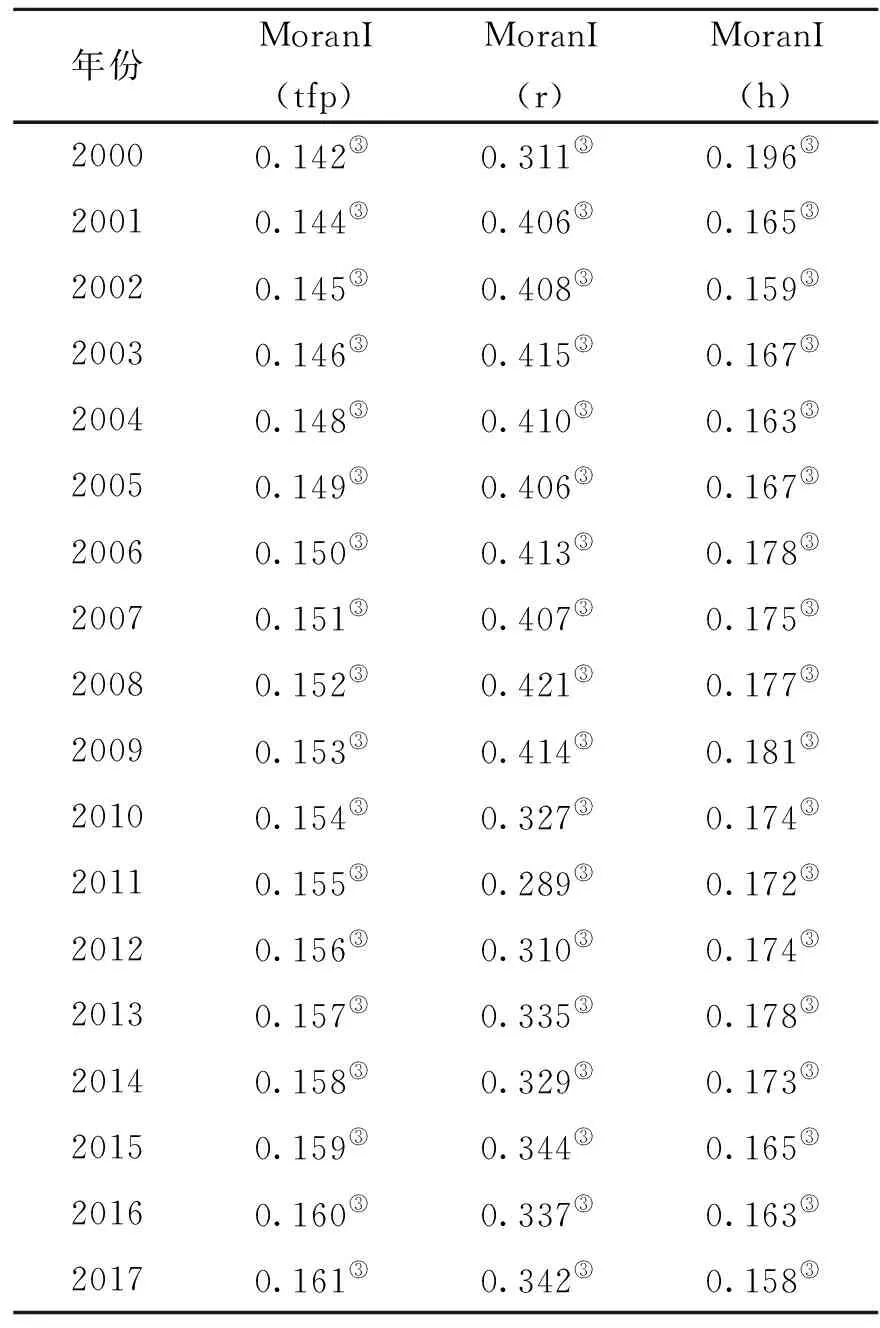
表1 2000-2017年重要变量全局空间自相关性检验

使用Moran I进行全局空间自相关性检验,可能会忽视在局部区域出现的反常状况或者局部的不稳定,如果需要确定某区域i附近的空间集聚情况,则需耍进行局部莫兰指数I检验。图1和图2分别为2000年和2017年被观测区域全要素生产率的局部莫兰I散点图。图中各样本分布基本保持一致,这与上文全局空间自相关性检验的结论相符。

图1 2000年我国各省全要素生产率局部Moran I散点图

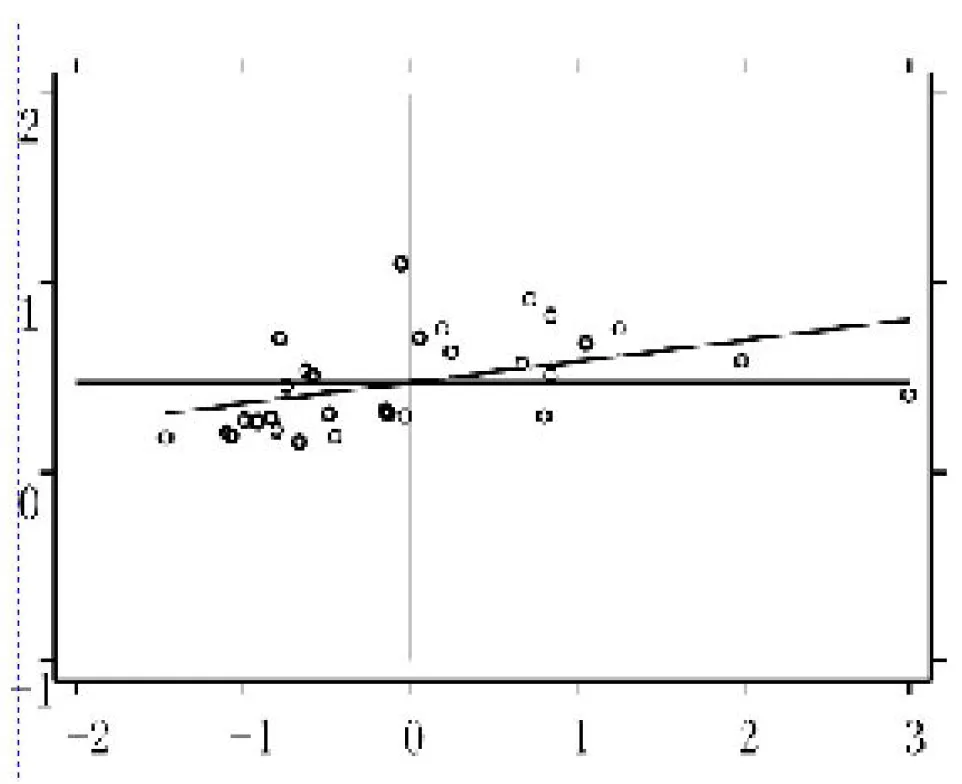
图2 2017年我国各省全要素生产率局部Moran I散点图

(三)空间计量模型的介绍及选择

空间计量模型的选择是实证分析的关键步骤,国内外常用的空间计量方法主要有三种。一种是将误差项的空间自回归过程加入传统的面板模型中,即空间误差模型(SEM);一种是在传统面板模型中加入因变量的空间滞后项,即空间滞后模型(SLM);还有一种是将因变量的空间滞后项和自变量的空间滞后项都加入到模型中,即空间杜宾模型(SDM)。

SDM模型可表示为式(2):

Y=ρWY+Xβ+WXδ+ε.
ε～N(0,σ2I)

(2)

其中,Y为被解释变量;X为一系列解释变量,包括核心解释变量和控制变量;参数β、δ为系数向量;W为空间权重矩阵,参数ρ为自回归系数,衡量样本区域间空间依赖性;空间滞后项WY是通过影响其他地区的生产率反过来影响本地区的生产率;空间滞后项WX表示本地被解释变量会受其临近区域的解释变量的影响,ε为随机误差项向量。由于空间自相关的存在,用传统的OLS方法来估计结果将不再准确。为解决这一问题,Elhorst发展了针对空间面板模型的极大似然估计方法[17],下面的分析将基于该方法。

对于如何选择模型,Elhorst[18]建议在模型中优先考虑因变量和自变量的空间相关性,而排除误差项的空间相关性,即先将模型设定为空间杜宾模型,再通过Wald检验是否可以简化为空间误差模型或空间自回归模型[18]。在此基础上,还要根据Hausman检验来确定固定效应和随机效应的选取。

表2为基于经济距离空间权重矩阵的空间杜宾模型的Wald检验以及LR检验结果。从表中可以看出空间自回归项(滞后项)的Wald检验在1%的水平上拒绝原假设(H0∶θ=0),说明空间杜宾模型(SDM)不能被简化为空间滞后模型(SLM),空间误差项的Wald检验在1%的水平上拒绝原假设(H0∶θ=-βλ),说明空间杜宾模型(SDM)也不可以被简化为空间误差模型(SEM)。另外,空间滞后和空间误差的LR检验都在1%的水平上拒绝原假设,说明空间杜宾模型不可以被简化为SLM或者SEM。针对固定效应模型与随机效应模型的选择,Hausman检验也在1%的水平上拒绝模型为随机效用模型的原假设。因此,最终选择固定效应空间杜宾模型。

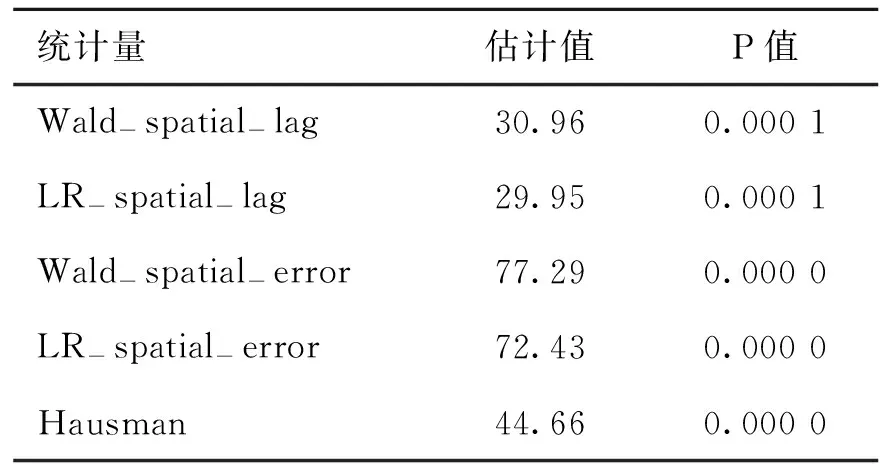
表2 Wald统计量和LR统计量

(四) 数据说明

本文选取我国除港、澳、台地区和西藏自治区外的30个省级行政区域为研究样本,研究期间为2000-2017年。所有原始数据均来自于《中国统计年鉴》(2001-2018)、《新中国60年统计资料汇编》及各省市《统计年鉴》(2001-2018)、《中国国内生产总值核算历史资料(1992-1995)》以及《中国国内生产总值核算历史资料(1952-2004)》。

对于被解释变量全要素生产率,本文选用常见的柯布—道格拉斯生产函数形式的随机前沿面板模型,并利用软件Frontier4.1计算得出。

产出变量采用国内生产总值(GDP)作为衡量经济增长的基本指标。以2000年不变价为基期,对2000-2017年的数据进行平减。投入变量包括资本存量和劳动力。物质资本存量用永续盘存法对2000-2017年我国各省级地区物质资本存量进行估计。永续盘存法具体形式如式(3)所示:

Kit=Kit×(1-δ)+Iit.

(3)

其中,Kit和Ki(t-1)分别表示第i个地区在第t和t-1年的不变价物质资本存量;Iit为第i个地区在第t年的不变价的物质资本投资额;δ为折旧率。模型中各指标选取与计算参考张军采用的方法[19];物质资本投资额Iit使用固定资本形成额时间序列数据;基期资本存量选定为2000年资本存量,具体利用2000年资本形成总额除以10%得出2000年的资本存量数据;折旧率根据已有相关研究文献设定为9.6%,投资价格指数采用各省的固定资产投资价格指数,劳动投入采用各省统计年鉴中的年末就业人数。

通过构建随机前沿生产函数,计算整理各样本区域技术效率值,可得到我国各省在样本期间的全要素生产率平均值如表3所示(表中数据由作者根据计量结果整理获得)。全要素生产率均值的前十名城市为上海、天津、北京、辽宁、江苏、福建、广东、浙江、黑龙江和内蒙古,基本都是交通比较发达的东部沿海省份。全要素生产率均值的后十名城市为云南、甘肃、宁夏、贵州、广西、陕西、青海、四川、安徽和河南。基本都是交通比较落后的中西部地区。

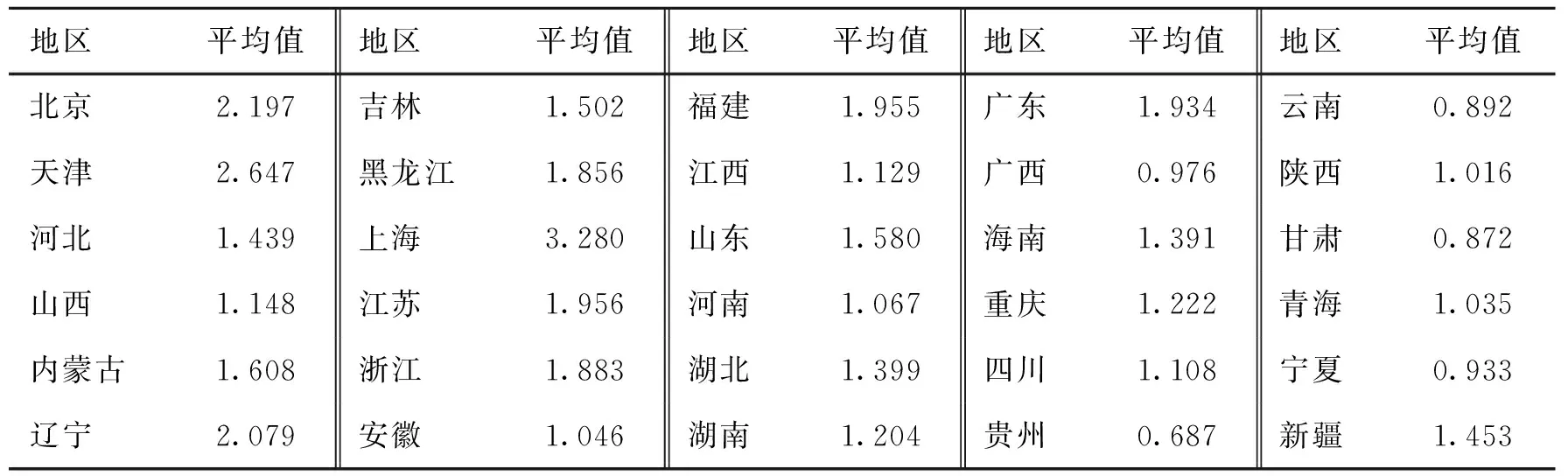
表3 各省市2000-2017年全要素生产率平均值

对于核心解释变量的选择,本文研究的重点是交通基础设施对全要素生产率的影响。我们倾向于用实物形态的变量来对交通基础设施予以代理。本文的实证分析以公路和铁路这两者为代表来研究交通基础设施对中国全要素生产率的影响。结合数据的可获得性,在自变量数据中,本文所考察的交通基础设施包括铁路密度和公路密度两项。其中,铁路密度(railway)采用“每平方公里的营运铁路里程”指标,这主要是考虑到营运里程这一统计口径反映了实际投入经济活动的铁路设施资源量,较之“铁路线路长度”的统计口径剔除了铁路设施的闲置部分,更适于服务本文的研究目的;公路密度(highway)为“每平方公里的公路通行里程”。为了考察交通基础是设施的联合影响,我们构建公路和铁路的交叉项RH来考察交通基础设施对全要素生产率的联合影响机制如下:

ln(tran)=α1ln(railway)+
α2ln(highway)+α3ln(RH),

(4)

ln(RH)=ln(railway)+ln(highway).

(5)

为了探究交通基础设施对全要素生产率的联合影响机制,我们通过式(2)分别对公路基础设施和铁路基础设施求偏导数:

(6)

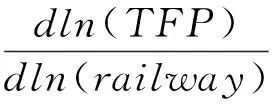
(7)

可以发现,交通基础设施对全要素生产率的影响已经不再相互独立,而是取决于两者的共同影响。只有α3为正时,才能发挥交通基础设施之间优势互补的协同效应,从而更有力促进全要素生产率的发展。

对于控制变量的选择,本文采用人均受教育年限表示我国的人力资本(hum)。人均受教育年限参考彭国华[20]把劳动力平均受教育程度分为文盲半文盲、小学、初中、高中、大专及以上,其平均受教育年数分别设定为1.5年、6年、3年、3年、3.5年。根据教育年限法的计算公式,劳动力平均接受教育年数=文盲、半文盲的就业人口比重*1.5+接受小学教育的就业人口比重*7.5+接受初中教育的人口比重*10.5+接受高中教育的人口比重*13.5+接受大专及以上的就业人口比重*17。本文用外资依存度变量(FDI)来衡量一个城市的资本开放程度。外资依存度变量是各区域直接利用外商投资额与当年该地区生产总值之化,其中进出口贸易总额和FDI均用当年年均汇率转换成人民币进行计算。城市化在区域经济增长中发挥着重要作用,把城镇人口在总人口中所占的比重作为城市化率(urban)的指标。

(五) 模型估计

本文实证模型的具体形式如式(8)所示:

ln(TFPit)c+λWln(TFPit)+αTln(tranit)+βTln(CVit)+φTWln(tranit)+γTWln(CVit)+εit.

(8)

其中,TFPit为样本省份i在第t年的全要素生产率,W为空间权重矩阵,tranit为样本省份i在第t年的交通基础设施存量,CVit为样本省份i在第t年的控制变量,εit为误差项且εit～N(0,σ2I)。虑到边际递减规律在现实经济活动中普遍存在,模型中的变量一律采用对数形式。

估计结果如表4所示,表中分别列出了采用时间固定模型、空间固定模型以及时间—空间双固定模型对交通基础设施与全要素生产率相关关系进行实证检验的估计结果,括号中为t统计量。三种模型的对数似然值分别为-115.435、507.395、564.452。在目前己有的研究中,在模型的选择方面我们主要通过对数似然值来判断。对数似然值Log-Likelihood越大,模型的解释性越好。可见双固定效应模型的对数似然值是最大的,这与上文的检验结果得出了一致的结论。因此本文将选择地区时间双固定的空间杜宾面板模型对我国交通基础设施全要素生产率之间的关系进行实证分析。

根据表4中双固定模型估计结果,空间滞后项W*lnTFP的系数为正值且通过了5%的显著性水平检验。铁路基础设施变量lnrailway与公路基础设施变量lnhighway的系数均为正值并分别在1%和10%的显著性水平下通过了显著性检验。交通基础设施的联合影响因素lnRH也显著为正,说明铁路和公路基础设施与本地的全要素生产率之间存在明显的正向相关关系,交通基础设施的完善促进了本地全要素生产率的增长。

表4 基于经济距离空间权重矩阵的空间杜宾模型估计结果

铁路基础设施的空间滞后项W*lnrailway的系数为正且在1%的显著性水平下通过了检验,说明在考察期间内我国各省级区域铁路交通基础设施与其周边邻接区域的全要素生产率之间存在明显的正相关关系。公路基础设施的空间滞后项W*lnhighway系数为负值且不显著,说明周边地区公路基础设施对本地区的影响不明确。滞后项W*lnRH的溢出效应为负且显著,说明铁路公路基础设施都发达的地方其虹吸效应比较大,反而不利于周边地区的发展。

本文选取的控制变量中,人力资本(hum)、外资依存度(FDI)对当地的影响和人力资本(hum)滞后项对邻近地区的影响都通过了显著性检验,并且系数都为正。表明人力资本和外资依存度不仅对本地区的全要素成产率有正向促进作用,邻近地区的人力资本对本地区全要素生产率水平也有显著促进作用。

直接效应是指解释变量的变化对本地全要素生产率影响的平均值,间接效应是指解释变量的变化对非本地区域全要素生产率这一间接影响的平均值,二者之和为总效应。总效应是指解释变量的变化对所有被观测区域全要素生产率影响的平均值。

表5中的结果显示,铁路基础设施的增长对区域全要素生产率的直接效用、间接效用和总效应均在在1%的水平上显著且为正值,说明在实证考察期间铁路基础设施的增长不仅会促进当地的全要素生产率增长,也显著促进了邻近地区全要素生产率的增长。公路基础设施的直接效用在10%的水平上显著为正值,间接效用和总效用为负值且不显著,说明在实证考察期间公路基础设施的增长对本地全要素生产率的具有显著的促进作用。铁路和公路基础设施的交叉项RH表示铁路和公路的共同作用,其对全要素生产率的直接效应为正且显著,间接效应和总效应为负且显著,说明本地公路和铁路的联合发展对邻近区域的发展是起一定的阻碍作用的,邻近地区要想更好的发展,也需要具备良好的交通基础设施。各控制变量中只有人力资本的各个效应显著为正,说明人力资本对全要素生产率的增长起到了毋庸置疑的促进作用。

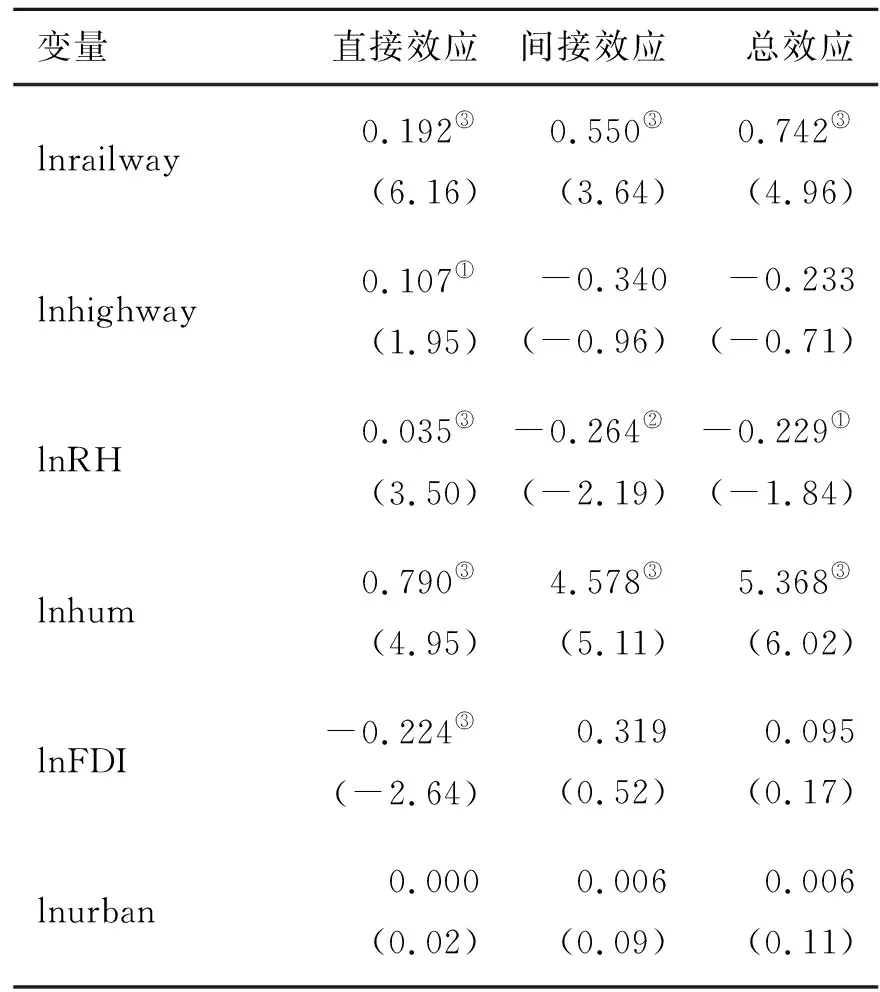
表5 双向固定效应SDM模型的直接效应、间接效应和总效应

四、结论及政策建议

本文以2000-2017年中国30个省市为研究对象,利用近期发展的空间杜宾模型分析并检验基础设施与区域全要素生产率的关系。通过研究发现公路和铁路的发展完善都可以在一定的水平上促进区域经济体全要素生产率的增长,尤其是铁路里程的不断增加,不仅可以促进当地的效率水平而且还可以带动其他沿线地区的经济增长。其空间上的溢出效应十分明显,充分发挥了公共物品正外部性的有利特征,同时也验证了国家近年来大力发展高速铁路的远见卓识。

虽然,我们应该大力发展铁路基础设施,但是公路的发展也不可忽视,而且公路和铁路的相互补充,可以发挥出整体的协同效应。公路的空间溢出效应并不明显,说明在我国各内陆省份之间,公路的连通性并没有发挥出带动作用,其会显著带动当地的发展,但是没有一定的溢出效应。从公路和铁路的交互影响指标RH可以看出,公路和铁路的同时发展,会更好的促进全要素生产率的增长,其中任一个发展滞后都可能对经济产生负面的影响。为了发挥交通基础设施之间的整体协同效应,公路发达铁路不发达的省份,更需要促进铁路的发展,因为铁路的带动作用更强。

本文结果对于政府公共支出政策选择具有一定的参考价值:其一,由于基础设施具有空间外溢特征,政府在进行公共资源配置时,应充分考虑省市间交通基础设施的合理布局,进一步加快中西部地区交通基础设施的建设,有效促进落后地区物质资本和人力资本的持续改善;其二,考虑到交通基础设施作为公共物品,在有限的资源条件下,政府应合理安排各项公共支出,提高投资效率,在加强交通基础设施建设的同时,进一步提高落后地区的教育、科研和医疗条件,全面促进落后地区的发展,若只发展交通基础设施可能只会阻碍这些落后地区的发展。

总之,政府应该大力推动区域间的协调、全面和可持续发展。