新型冠状病毒肺炎在职业院校人群动力传播规律分析

谭 平

(陕西铁路工程职业技术学院铁道工程系，714000，陕西，渭南)

0 引言

新型冠状病毒肺炎(简称COVID-19)是一种动物传染人、人传染人及相互传播的疾病，自从2019年12月26日至今，传染速度之快，给中国乃至世界，造成巨大恐慌，严重影响我国人民生命和财产安全，为此，我国成立疫情防控小组，利用各种手段控制疫情蔓延[1]。因此，全面认识COVID-19的发病机理、了解病毒的传播规律，提出有效防控策略，关系国计民生, 这也是当前世界乃至后期一段时间所面临且迫切需要解决的热点问题[2]。对于不同种群间传播规律的研究具有理论和社会意义。对于高职院校学生(特定种群)而言，与普通种群，他的聚集性高、交叉大，与本科院校相对，学生理论基础较差，好动程度强[3]，且在校大部分时间是在校内外实训(实习)[4]，被感染和交叉感染风险大。对于传染病传播动力模型规律认识，最早是200年前，科学家Bernoulli 建立了天花传播模型[5]，随后Kermack建立了“阈值理论”[6]；据此，胡志兴[7]建立了SIRS分布时滞和非线性接触率。郭宝珠[8]利用Bernoulli阈值建立了一个年龄结构分布控制传染病模型。胡杰[9]等根据投放染病害虫、天敌和喷洒化学农药的传染病模型研究发现，传染病传播过程中符合脉冲微分方程小振动理论。目前对于传染病，大部分针对的是病原个体、禽人间、人人间传播，没有考虑人与人、人与禽间的混合型，混合型中还包括类聚性[9]。本文传统的阈值动力学模型理论为基础，依据陕西铁路职业技术学院COVID-19上报数据，考虑高职院校不同年级学生活动轨迹及聚合性、关联度等因素，建立传染病在高职院校间传播的模型，通过再生系数的矩阵方程，判定模型稳定性，分析COVID-19在职业院校中不同年级间的传播规律。

1 职业院校COVID-19关联函数建立

高职院校管理相关规定，学生大体分为3类，大一、大二、大三，特点是大一集体活动多，大二专业实践课程多，大三大部分学生在自己所签订单位顶岗实习，中途回来4～5次，在学校停留时间在1—3周，大一、大二、大三间交流主要是通过学生工作办公室、辅导员及相关班委。根据Kermack舱室理论，不考虑开除、留级及意外死亡等因素影响，群体间不进行任何交流联系，可建立职业院校传染病网格示意图1。

图1 高职院校传染病网格示意图

假设群体以班级为单位，每一个班级为一个独立的舱室，每一个年级种群关联度不同可设种群列j，每一个班级中群体包括正常者Fs，感染者FI及治愈者FV，可设置为行i，每一班级在一个节点上，班级中感染数量关系见公式(1)：

(1)

感染速率λ及治愈速率γ，感染后移除舱室，假设治愈后不再感染，传染经过时间[t,t+△t]，感染与治愈者按照公式(2)：

λ·△t，γ·△t

(2)

相应的正常种群减小量及增加量见公式(3)：

λ[Fs·FI]△t|γFI△t

(3)

大三顶岗实习归来学生进入舱室，设定为新进种群，网格数量增加bN(t)△t,以入网络的节点 k 的易感、恢复者可表示为公式(4)：

(1-p)bN(t)π△t;pbN(t)π△t

(4)

新增加节点进入原有网格后，度会增加1，经过时间t后，由此增加n个后可设置为公式(5)[2]：

(5)

建立传播动力微分方程见公式(6)：

(6)

加入一个人被感染，网格中原来是S-S将变成I-S，则I-S边可以增加率为[2](1-p)φ′(1)[FI]，则边界方程满足公式(7)：

(7)

2 基本再生指数

动力模型中，处于无感染极限时，则有FM=0，FI=0，令式(6)、式(7)右边等于0，可得雅克比矩阵(8)：

展开后

(8)

解非其次线性方程组，矩阵下部化简，特征方程见公式(9)：

(9)

其中，显然x=b=-2b=0都是方程组一个根。

当公式(10)

(10)

特征方程具有负实根，J区域稳定。

由此得到种群再生系数，

无病平衡点E0趋于稳定。

模型中，当新进成员为零时，也就是新引进成员为零时，即p、b都趋于0时，模型就变成了Lindquist静止模型，根据Lindquist设定系数，φ′(1)=5.7，φ″(1)=68.432，α=4.669，γ=0.1-1，λ=10-50。

静态动力模型中，基本再生系数与感染系数和治愈系数关系如图2所示，据图2分析可知，再生系数随感染系数增大而增大，但再生系数小于并无线接近于1，随着治愈系数增加，再生系数逐渐减小，接近于0 ，对于再生系数小于1，模型处于不稳定状态，说明，Lindquist静止模型有一定局限性。对于网格动力模型中，再生系数与感染系数和治愈系数关系如图3所示，与静止模型规律基本相似，感染系数在30～50之间，再生系数稳定且大于1，说明，本文建立模型适合于传染病动力再生规律分析。

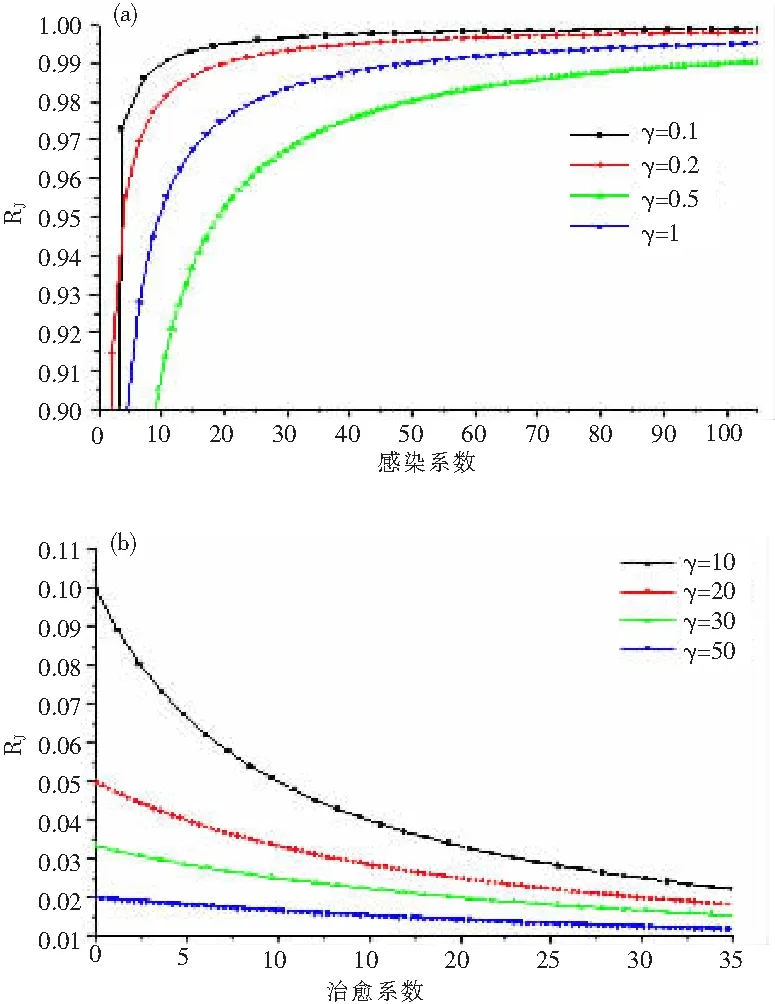
图2 Lindquist静态模拟结果

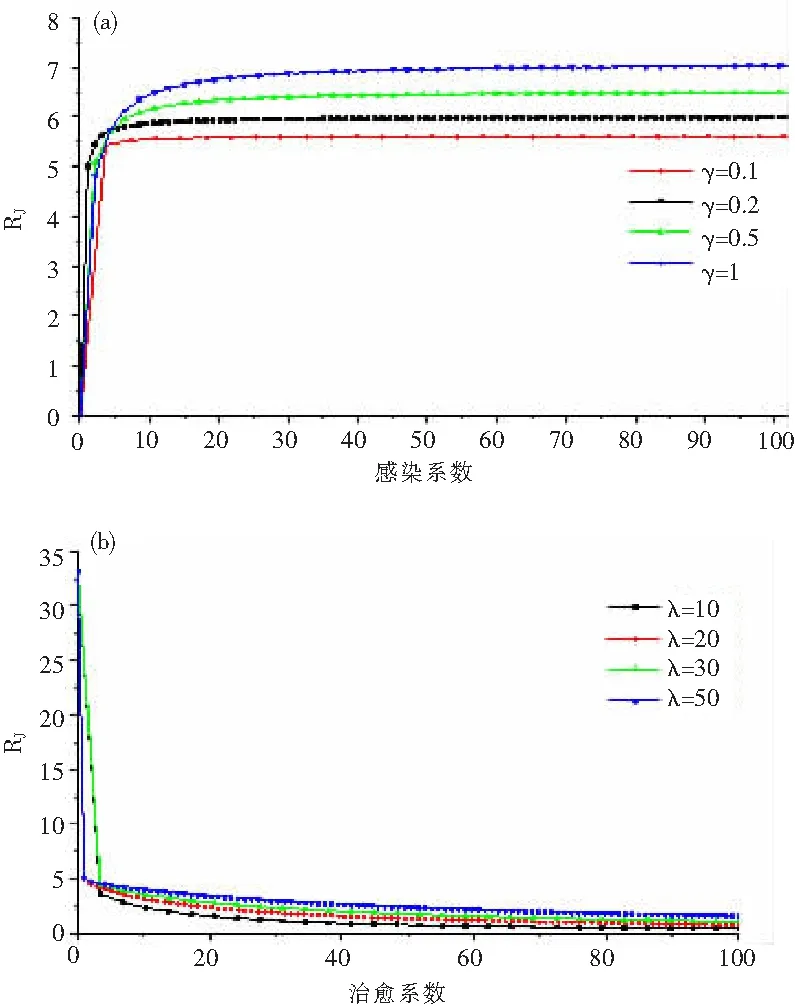
图3 网格模拟结果

3 职业院校疫情防控措施评估

疫情源于武汉(可能源于华南海鲜市场)，截止2020年2月20日，我国COVID-19感染人数如图4所示。通过感染云图分析，目前总计62 254人，其中，湖北60 000人，从数据看属于疫情高发区，陕西省232人，属于蓝色疫情防控区，属于人与人间的被传播(与湖北密切接触者)，其中，渭南市15例，在陕西属于中度防控区，截止2月20日，统计新增种群如图5所示，因为大一、大二在校期间，与渭南市疫情种群增加类似，采用指数增长模型。

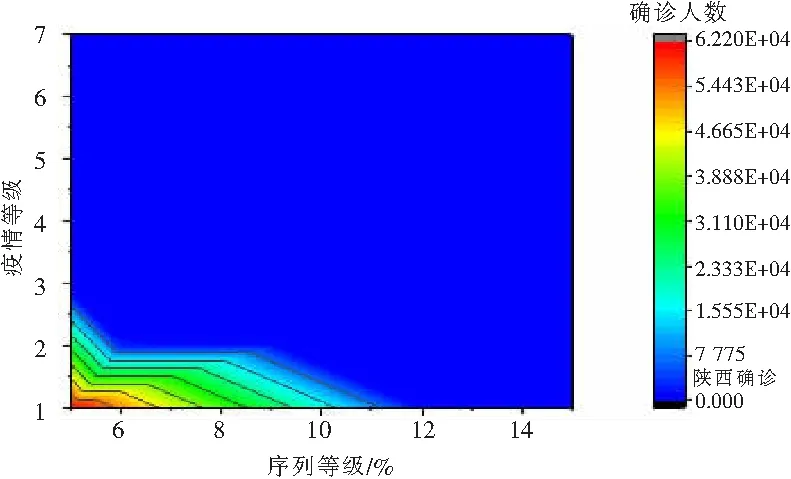
图4 2020年2月20日全国确诊分布

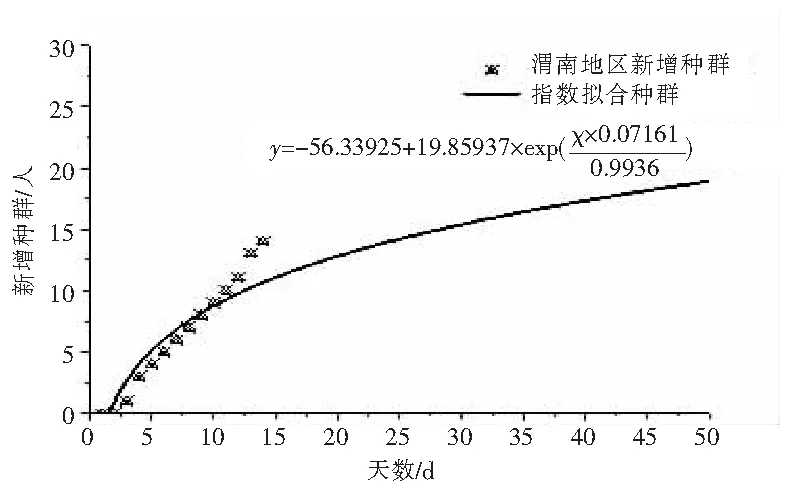
图5 大一、大二疫情种群预测图

根据目前学校统计报告及我国防控中心数据，将动力模型系数确定如下。

1)大三情况统计如图6所示，大三因为80%以上学生都去参加顶岗实习，与外省人员接触密切，假设大三在校生只要进入武汉的学生或者与湖北密切接触学生就认为是被感染者，目前陕西铁路工程职业技术学院共计有34人，其中在武汉参加医疗工程建设任务的3人，17人回家，23人有返校经历，大一按舱室值确定，大二按照渭南指数增长模型推算，感染累计疫点数n= 1.637×107，感染系数可以定义为γ=0.8，1，1.2，治愈系数为λ=30.2，37.2，40.4。

图6 职业院校大三进仓风险增加原因

2) 从学生返仓原因可以预测出他们返仓轨迹。假设返校、违约学生与离校生在同一时间发生，可得到φ″(x)≈κφ′(x) ，据此估算出p=10%。

3) 因为后期除了舱室隔离，还有有疫苗作用，因为COVID-19病毒没有疫苗，参照H5N1 禽流感灭活疫苗资料显示，免疫保护为 1 a，因此设失效率φ= 1。其他参数假设为q=0.2，α=0.03，β=0.6。

图7 为病情一个周期段内、高职院校不同年级下以班级为舱室下累计感染模型，从种群进入网格数量分析不同，随着年级增长，感染系数增大，感染人数也在增加，随着舱室隔离、疫苗等作用，感染人数最终下降，最终趋势值基本相同。

图7 预测职业院校传染病传播规律

4 结论

为了深入研究COVID-19在职业院校学生间传播，做好学生返校后疫情防控，保障学校正常教学、生产复工，建立网格传染病防控模型，可得到以下规律。

1)通过舱室理论建立以班级为单位的舱室；通过辅导员、学生间联系及高职院校各年级特点，设定职业院校传染网、学生感染系数及治愈系数；通过网格高斯理论，建立了COVID-19微分动力方程。

2)通过雅克比矩阵解线性方程组，通过简化判定，雅克比矩阵J为负，说明基本再生系数大于1，动力微分方程稳定，比Lindquist静止方程更加适用。

3)通过对全国COVID-19疫情判定，陕西省处于被感染区，陕西铁路工程职业技术学院所处的渭南市在陕西省属于中度防疫区，由于职业院校大一、大二学生特性，采用渭南地区指数增长模型，大三采用倍数增长模型，通过不同种群模型参数，建立一个周期内，防疫模型，通过模型分析，大三学生在外实习感染风险较高，但随着隔离、疫苗等手段控制后，疫情发展终值基本相同。