面向深度神经网络的安全计算协议设计方法

毕仁万，陈前昕，熊金波，刘西蒙

面向深度神经网络的安全计算协议设计方法

毕仁万1，陈前昕1，熊金波1，刘西蒙2

(1. 福建师范大学数学与信息学院，福建 福州 350117；2. 福州大学数学与计算机科学学院，福建 福州 350108)

针对深度神经网络模型计算过程中存在的信息泄露问题，结合加性秘密共享方案，在两台非共谋的边缘服务器间设计安全高效的交互计算协议。考虑到非线性函数不能直接拆分，首先提出一组基本转换协议，实现加性副本和乘性副本的安全转换，经过少量调用，可以安全计算幂函数、比较、指数、对数、除法等底层函数。由于数据传递和计算特点，协议可以扩展至数组计算。理论分析证明了协议的正确性、高效性和安全性，实验结果表明，协议具有较小的误差，其计算和通信开销均优于现有设计方案。

深度神经网络；加性秘密共享；安全计算协议；加法−乘法转换；数组单元

1 引言

随着人工智能和物联网时代的全面到来，智能终端设备被赋予自主采集各种类型数据的能力，如高清摄像机捕捉图像数据、声学设备采录语音数据、LiDAR设备探测点云数据[1]等。为了进一步挖掘、分析出有意义的信息，相比传统的机器学习算法，采用深度神经网络模型处理数据可以获得更高的预测精度。例如，Ren等[2]利用卷积神经网络提取图像目标的特征信息，Zhou等[1]采用稀疏卷积神经网络提取云目标的特征信息等。然而，深度神经网络由于模型深度、参数数量等特征会耗费高额的计算开销，资源受限的智能终端选择将数据和任务需求提交给边缘服务器进行处理。随着数据控制权的迁移，包含在数据内的隐私信息存在极高的泄露风险，如何在不泄露隐私信息的前提下快速准确地将原始数据分析转化为有价值的内容，是当前应用研究的热点。

实际上，隐私信息是否安全可以归结于网络函数计算的安全性，目前，主要结合同态加密[3]和加性秘密共享[4]方案构思解决方法。同态加密概念自提出以来被广泛应用于密文处理，Hesamifard等[5]通过构造非线性函数的低阶近似多项式，采用线性同态加密可以实现线性修正单元（ReLU）、双曲正切（Tanh）、Sigmoid等网络激活函数的密态计算，但烦琐的加密计算开销难以满足智能终端低延迟性需求。针对这一问题，Mohassel等[6]最早将加性秘密共享概念引入线性回归、逻辑回归和神经网络等模型训练任务中，基于安全两方计算[7]提出了一系列隐私保护协议，相比同态加密算法提高了计算效率。随后，唐春明等[8]针对两台非共谋服务器训练线性回归模型过程中的信息泄露问题，结合加性秘密共享设计了安全加法、乘法交互计算协议，并将Sigmoid激活函数中的指数函数展开为泰勒多项式形式，利用加法和乘法计算协议可以获得其近似值。然而，这些协议采用不经意传输机制[9]传递数据，并且需要多轮近似迭代计算，计算效率较低，并且没有分析协议的误差范围。显然，神经网络模型的正确性和效率依赖于底层计算函数，刘新等[10]探索基本初等函数的安全高效计算方法，终端将模糊化的数据传递给云服务器，由两者共同计算目标函数的结果，计算复杂度降低为常数阶，并且设计的计算协议可以扩展至数组计算，但计算过程需要终端同步参与数据传递。

近年来，研究学者结合加性秘密共享在隐私保护神经网络方面取得较大进展，Huang等[11]提出了一种隐私保护图像特征提取方案，设计的安全比较函数可以正确实现ReLU激活函数功能。Ma等[12]提出了一种隐私保护语音识别方案，利用长短期记忆网络提取关联语音特征信息，设计的安全Sigmoid函数和Tanh函数可以实现门控的迭代计算。Liu等[13]提出了一种隐私保护图像目标检测方案，设计的安全指数、对数和倒数计算协议可以正确实现检测网络的底层函数功能。这些安全计算协议可以为网络模型提供足够的安全性，遗憾的是，需要多轮迭代[14]降低误差以达到计算精度需求，计算开销依赖于迭代次数。

为了克服上述安全计算协议的缺陷，本文面向深度神经网络底层函数探索安全高效的计算协议设计方法，主要贡献总结如下。

1) 考虑到非线性函数拆分困难的特性，设计了安全乘法-加法转换（STMA，secure transforming multiply-add）和安全加法-乘法转换（STAM，secure transforming add-multiply）协议，实现加性副本与乘性副本的安全等值转换。

2) 在安全转换协议的基础上，结合基本运算性质可以实现对非线性函数的计算拆分，设计的安全幂函数、比较、指数、对数、除法等计算协议不需要引入复杂迭代操作，并且可以扩展至数组计算。协议的输入和输出仅需要加法计算完成拆分与合并，构建安全的深度神经网络模型可以自由选择和替换固有的函数模块。

3)详细的理论分析证明了所提协议的正确性和安全性，并且计算和通信复杂度可以控制在常数阶。实际性能测试结果表明，协议的误差在可接受范围内，计算和通信效率均优于最新的研究工作。

2 系统模型与安全模型

2.1 系统模型

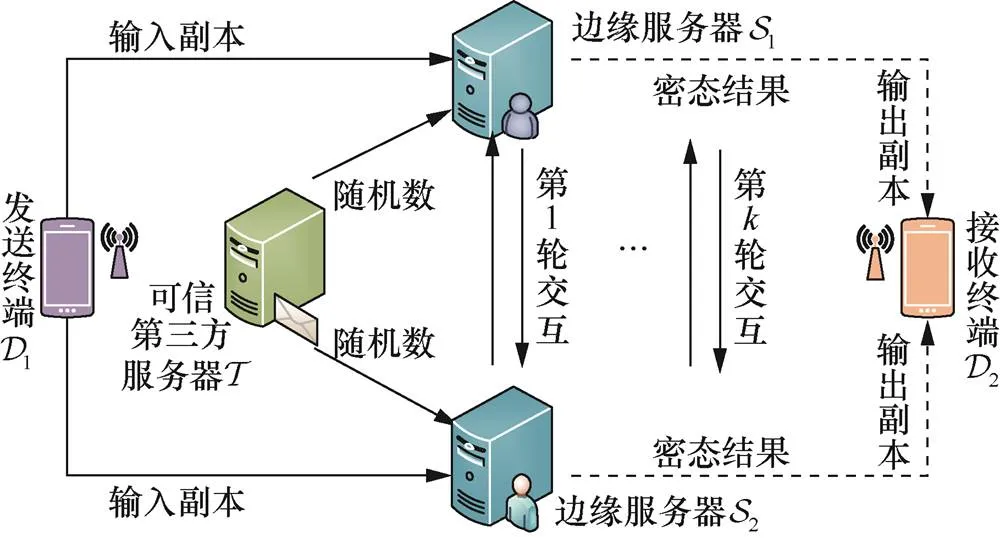
图1 系统模型

Figure 1 System model

2.2 安全模型

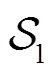
3 基本安全转换协议

3.1 安全乘法-加法转换协议

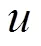
协议1 安全乘法-加法转换

3.2 安全加法-乘法转换协议

协议2 安全加法-乘法转换

4 安全协议设计方法

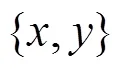
4.1 安全幂计算协议

4.2 安全比较计算协议

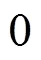
4.3 安全指数与对数计算协议

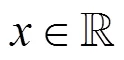
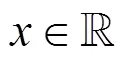
4.4 安全除法计算协议

5 理论分析

5.1 正确性分析

第3和第4节的诸多协议是针对深度神经网络模型需求而设计的，正确性是计算协议可行性的一部分，接下来，本节提供详细的推导过程证明协议的正确性。

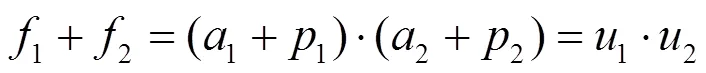
5.2 复杂度分析

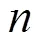
表1 协议的计算复杂度比较

注：表示输入数组长度；表示二进制位长度；表示子协议迭代次数

表2 协议的通信复杂度比较

注：表示二进制位长度；表示子协议迭代次数

5.3 安全性分析

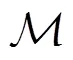
引理1 若协议调用的所有子协议在多项式时间内是可模拟的，那么该协议是可模拟的。

定理1 在半可信模型中，STMA和STAM协议是安全的。

证毕。

定理2 在半可信模型中，SPow、SRec和SMul协议是安全的。

证毕。

定理3 在半可信模型中，SComp、SExp、SLog和SDiv协议是安全的。

证毕。

6 协议性能分析

6.1 误差分析

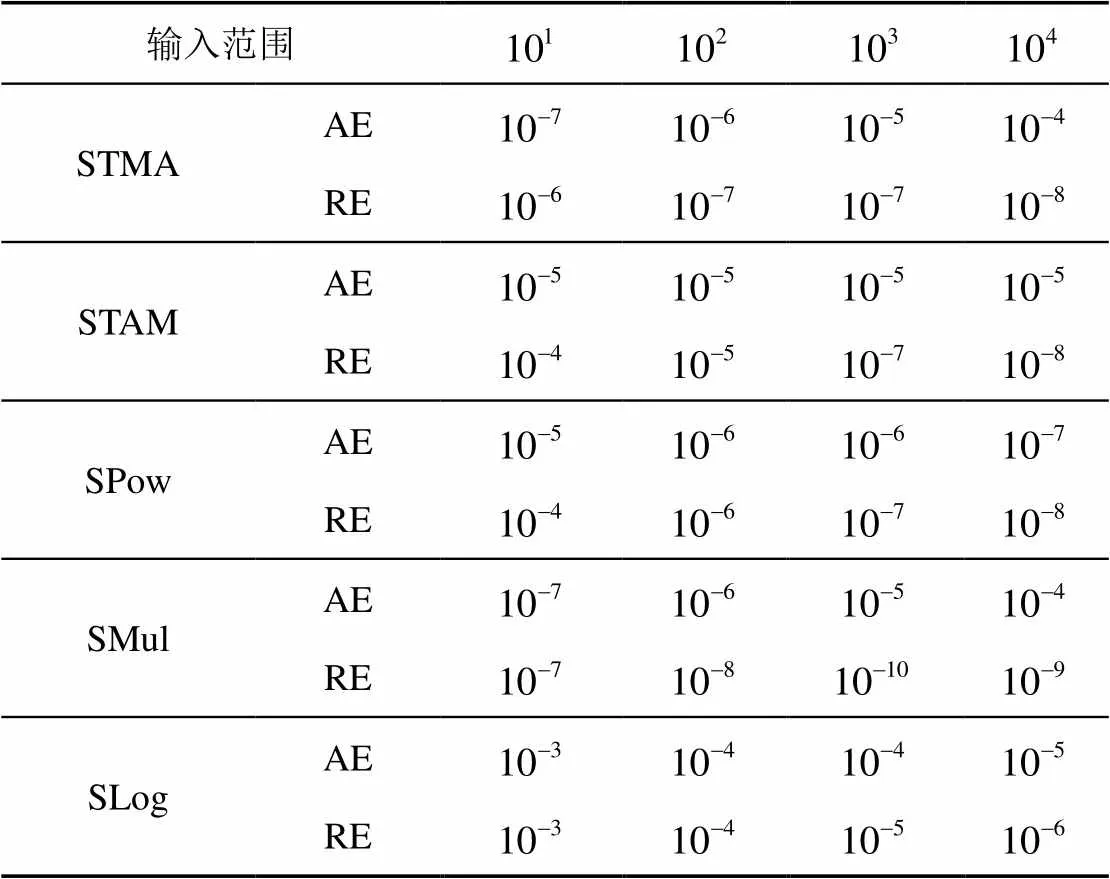
表3 协议的绝对误差和相对误差

6.2 实际开销分析

6.2.1 计算开销

6.2.2 通信开销

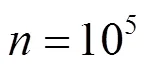
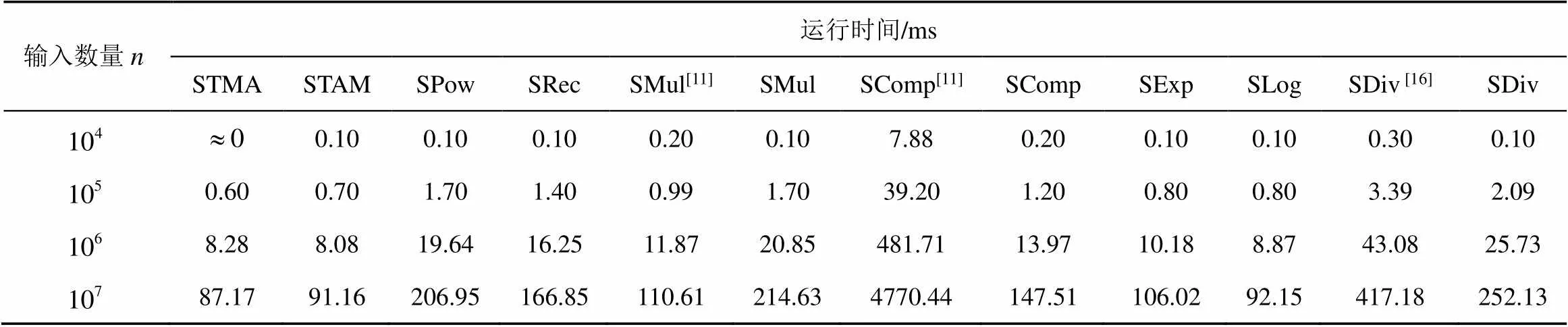
表4 协议的计算开销

表5 协议的通信开销

7 结束语

智能终端由于自身资源受限，选择将复杂的深度神经网络模型计算任务卸载至边缘节点。考虑到计算过程的安全性，本文为网络底层函数量身设计了一系列安全计算协议，可以扩展至数组计算，不需要迭代操作即可实现函数的线性分割，两台非共谋边缘服务器及潜在敌手均不能获得完整的输入和输出。经过实际性能评估，协议的计算误差可以忽略不计，并且计算和通信开销均优于现有工作，十分适合深度神经网络函数的安全替换。在未来工作中，将继续寻找进一步提升协议计算和通信效率的方法，同时设计更多通用函数对应的安全计算协议。

[1] ZHOU Y, TUZEL O. Voxelnet: end-to-end learning for point cloud based 3d object detection[C]//The IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2018: 4490-4499.

[2] REN S Q, HE K, GIRSHICK R, et al. Faster R-CNN: towards real-time object detection with region proposal networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 39(6): 91-99.

[3] YANN L, BERNHARD B, JOHN S D, et al. Backpropagation applied to handwritten zip code recognition[J]. Neural Computation, 1989, 1(4): 541-551.

[4] XIONG J B, BI R W, SZHAO M F, et al. Edge-assisted privacy-preserving raw data sharing framework for connected autonomous vehicles[J]. IEEE Wireless Communications, 2020, 27(3): 24-30.

[5] HESAMIFARD E, TAKABI H, GHASEMI M. CryptoDL: deep neural networks over encrypted data[J]. arXiv preprint arXiv:1711.05189, 2017.

[6] MOHASSEL P, ZHANG Y P. SecureML: a system for scalable privacy-preserving machine learning[C]//IEEE Symposium on Security and Privacy (S&P). 2017: 19-38.

[7] YAO A C. Protocols for secure computations[C]//The 23rd Annual Symposium on Foundations of Computer Science (SFCS). 1982: 160-164.

[8] 唐春明, 魏伟明. 基于安全两方计算的具有隐私性的回归算法[J].信息网络安全, 2018(10): 10-16.

TANG C M, WEI W M. Regression algorithm with based on secure two-party computation[J]. Information Network Security, 2018(10): 10-16.

[9] RABIN M O. How to exchange secrets with oblivious transfer[J]. IACR Cryptology ePrint Archive, 2005:187.

[10] 刘新, 李顺东, 陈振华. 基本初等函数的保密云计算服务协议[J]. 计算机科学, 2015, 42(10):159-163.

LIU X, LI S D, CHEN Z H. Secure cloud computing service protocols of elementary functions[J]. Computer Science, 2015, 42(10): 159-163.

[11] HUANG K, LIU X M, FU S J, et al. A lightweight privacy-preserving CNN feature extraction framework for mobile sensing[J]. IEEE Transactions on Dependable and Secure Computing, 2019: 1.

[12] MA Z, LIU Y, LIU X M, et al. Privacy-preserving outsourced speech recognition for smart IoT devices[J]. IEEE Internet of Things Journal, 2019, 6(5): 8406-8420.

[13] LIU Y, MA Z, LIU X M, et al. Privacy-preserving object detection for medical images with Faster R-CNN[J]. IEEE Transactions on Information Forensics and Security, 2019: 1.

[14] VOLDER J E. The cordic trigonometric computing technique[J]. IRE Transactions on Electronic Computers, 1959, 8(3): 330-334.

[15] ZHU Y W, HUANG L S, YANG W, et al. Three new approaches to privacy-preserving add to multiply protocol and its application[C]//The 2nd International Workshop on Knowledge Discovery and Data Mining. 2009: 554-558.

[16] 李禾, 王述洋. 关于除法的安全双方计算协议[J]. 计算机工程与应用, 2010, 46(6): 86-88.

LI H, WANG S Y. Several secure two-party protocols of division[J]. Computer Engineering and Applications, 2010, 46(6): 86-88.

[17] BOGDANOV D, LAUR S, WILLEMSON J. Sharemind: a framework for fast privacy-preserving computations[C]//European Symposium on Research in Computer Security. 2008: 192-206.

[18] BOGDANOV D, NIITSOO M, TOFT T, et al. High-performance secure multi-party computation for data mining applications[J]. International Journal of Information Security, 2012, 11(6): 403-418.

Design method of secure computing protocol for deep neural network

BI Renwan1，CHEN Qianxin1，XIONG Jinbo1，LIU Ximeng2

1. College of Mathematics and Informatics, Fujian Normal University, Fuzhou 350117, China2. College of Mathematics and computer science, Fuzhou University, Fuzhou 350108, China

Aiming at the information leakage problem in the process of deep neural network model calculation, a series of secure and efficient interactive computing protocols were designed between two non-collusive edge servers in combination with the additive secret sharing scheme. Since the nonlinear function cannot be split directly, a set of basic conversion protocols were proposed to realize the secure conversion of additive and multiplicative shares. After a few invokes, the power, comparison, exponential, logarithm, division and other low-level functions can be calculated securely. Due to the characteristics of data transfer and computation, the proposed protocols can be extended to array computation. Theoretical analysis ensures the correctness, efficiency and security of these protocols. The experimental results show that the error of these protocols is negligible, and the computational costs and communication overhead are better than the existing schemes.

deep neural network, additive secret sharing, secure computing protocol, add-multiply transformation, array unit

TP393

A

10.11959/j.issn.2096−109x.2020050

毕仁万（1996-），男，湖南常德人，福建师范大学硕士生，主要研究方向为安全深度学习、安全多方计算。

陈前昕（1996-），男，福建泉州人，福建师范大学硕士生，主要研究方向为安全深度学习、隐私保护技术。

熊金波（1981-），男，湖南益阳人，博士，福建师范大学教授，主要研究方向为安全深度学习、移动群智感知、隐私保护技术。

刘西蒙（1988-），男，陕西西安人，博士，福州大学教授，主要研究方向为云安全、应用密码学、大数据安全。

：2020−04−17；

2020−07−03

熊金波，jinbo810@163.com

：国家自然科学基金（61872088, U1804263, 61702105, 61872090）；福建省自然科学基金资助项目（2019J01276）；贵州省公共大数据重点实验室开放课题（2019BDKFJJ004）

The National Natural Science Foundation of China (61872088, U1804263, 61702105, 61872090), The NaturalScience Foundation of Fujian Province, China (2019J01276), The Guizhou Provincial Key Laboratory of Public Big DataResearch Fund (2019BDKFJJ004)

论文引用格式：毕仁万, 陈前昕, 熊金波, 等. 面向深度神经网络的安全计算协议设计方法[J]. 网络与信息安全学报,2020, 6(4): 130-139.

BI R W, CHEN Q X, XIONG J B, et al. Design method of secure computing protocol for deep neural network[J]. Chinese Journal of Network and Information Security, 2020, 6(4): 130-139.