测量误差分析及数据处理若干要点系列论文（四）——统计学习理论及支持向量机方法统用于形位误差评定

林洪桦

测量误差分析及数据处理若干要点系列论文（四）——统计学习理论及支持向量机方法统用于形位误差评定

林洪桦

（北京理工大学，北京 100081）

阐述统计学习理论（SLT）及支持向量机（SVM）方法统用于形位误差评定。首先，简要复述SLT-SVM方法及特点；然后，详细描述多测点形位误差评定要点与难点、统用SVM方法基本依据及评定算法等；最后，验证现代数据处理对策四要诀：实、佳、智、验。

数据处理；数学模型；误差；统示法

系列论文[1-3]已述，在利用计算机分析处理现实问题时，在小样本下处理三非（非线性、非高斯、非平稳）问题应为常态，并多次推荐直接采用特殊到特殊的转导型推理方法，即按现有样本数据及所掌握有关先验信息直接估计和预测所求现实问题的某一待求结果。如，目标只是估计误差范围就无需估计其理论概率分布，应尽量降低求解要求，以获得更为准确、更合乎实际的待求结果。具体而言，可采用机器学习技术统计学习理论（statistiacal learning theory, SLT）及支持向量机（support vector machine, SVM）方法[4-5]。

误差评估方法和其他科技领域一样，传统上多基于特殊到一般再到特殊的归纳演绎推理方法，习惯于先求出误差的理论概率分布，再推论现实问题的某一待求结果。然而，实质上这是个不适定逆问题。在有限数据或小样本下，对概率分布统计推断的结果常与实际不符或相去甚远。应用基于转导推理的SLT- SVM方法所得到现实问题的某个估计、预测结果，可能更直接、更客观，而现实也就更准确。

1 SLT-SVM方法及特点

SLT是研究利用有限经验数据进行机器学习的一般理论；SVM是在SLT指导下解决实际问题的一般方法。当前对SLT-SVM的核心内容并不陌生，在文献[4]~文献[6]中已有论述。SLT-SVM是依据有限数据或小样本，基于VC（Vapnik-Chervonnenkis）理论按结构风险最小化（structural risk minimization, SRM）原则进行函数（二值或多值函数、回归函数、概率密度等）估计方法。在此，仅简要列出SLT-SVM方法基本特点。

1）适用于有限数据或小样本下函数估计。设样本为

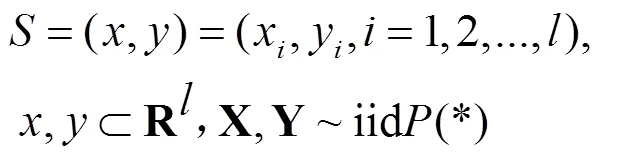
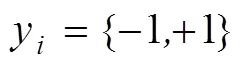
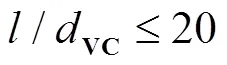
2）基于SRM原则。在有限样本下，真实风险与经验风险emp关系为

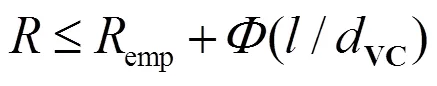
其后项与所估计函数的VC维有关，称为VC置信范围。若待估计函数类= {1,2,…,f}按其VC维递增排序，即VC(f-1) f)，则emp随之递减；反而随之递增。SRM原则就是所估计函数应使式(2)右端两项之和最小，以避免在单纯经验风险最小化下出现过拟合问题。SVM策略为在选定最小经验风险的某类函数结构中选出VC置信范围最小函数，其VC维也即支持向量的维数。

3） SVM方法具有全局优化性。SVM方法核心技术在于将现实问题转化成二次凸优化问题。同时，通过对偶优化处理使最优解只取决于少数构成支持向量的数据点，而与其他样本点无关，即具有稀疏性、稳健性。

4） SVM方法要点在于应用核函数技术。SVM源于最大间隔线性分类，即求解最大化两类样本间隔的分类最优超平面(−) += 0（平面内积表达式，其中= (1,2,…,w)T为法向向量；为法向偏置），仅为线性操作。将所要解决现实问题的数据样本通过核映射（不同现实问题选定的核函数各异），即非线性映射到高维特征空间，在该空间构造线性分类的最优超平面，使之简化为对应的线性操作，即为SVM核技术方法，支持向量分类（support vector classify-cation, SVC）通用式为[6]

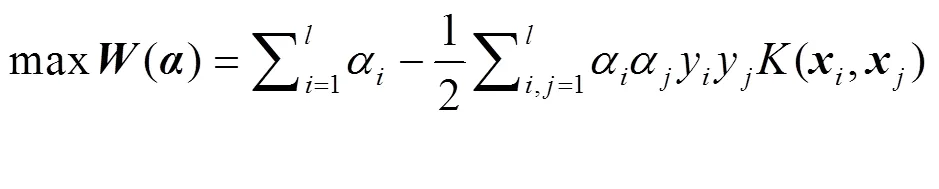
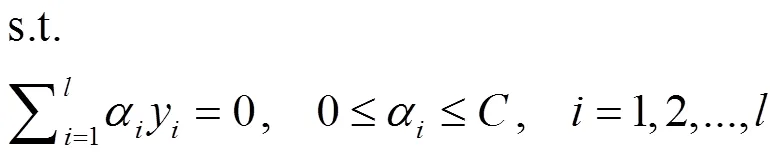
式中，为Lagrange乘子，即的对偶变量；(x,x) =(x)*(x)（*为内积）为的非线性核映射。

SVM通过引入不敏感损失函数，可推广应用于实函数估计的回归问题，支持向量回归（support vector regression, SVR）通用式为[6]

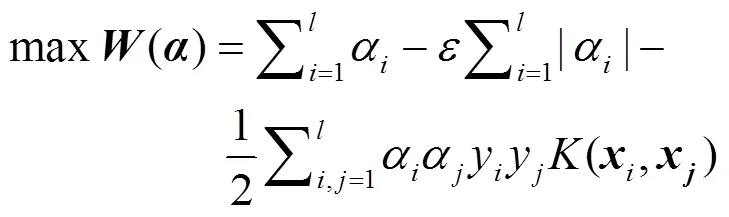
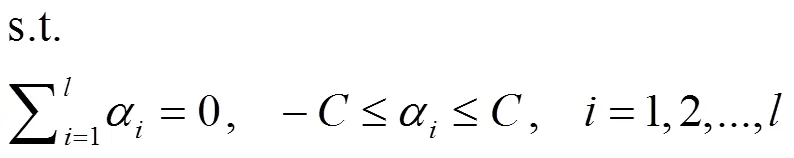
总之，SLT-SVM具有严格理论基础，在解决小样本、非线性、高维数等现实问题以及全局优化中具有特殊优势，尤其SVM仅以小支持向量集即可代表不同学习机器的整个训练集，并能推广应用到函数拟合等各种机器学习问题，且已具有LibSVM，LSSVM等应用软件。然而，SVM方法仍嫌复杂，近年来经不断改进、完善，包括简化、变形等，使之在许多专业领域渐多应用。

2　统用SVM方法评定多测点形位误差

一般形状与位置误差测量及评定方法多而杂，却难以适用于极值点较多的多测点情况。多测点形位误差的评定恰为现实难题之一，可统用SVM方法来解决。笔者于2011年已有统用SVM评定形位误差的设想，应华南理工大学刘桂雄教授之邀，协同指导其博士生基本上实现该设想[7]，验证统用SVM评定形位误差可行性。

2.1　多测点形位误差评定的要点及难点

在大尺寸或精细测量等情况下，常要求评定数据点> 50~100以上的多测点形位误差，其特点就在于“多”。

首先，形位公差国家标准规定形位误差评定按最小包容区域（minimum zone, MZ）原则。在MZ评定原则下形位误差仅取决于几个极值点，与其余数据点无关。在多测点下，形位误差极值点较多，尤其由于许多次极值点与极值点很接近，难以评定。

再者，按MZ原则评定形位误差本身就是难点。大多数形状误差并无明确的MZ评定准则，仅直线度、平面度、圆度等少数有MZ评定准则可依，空间形状误差则更难评定。位置误差对其基面而言，应先评定基面形状误差。可见，应以形状误差评定为基点，此亦为难点。

显然，对于多测点形位误差评定，未必力求合乎MZ评定准则，且多无准则可依。要点在于形位误差评定结果及其准确度应予验证。

2.2　多测点形位误差评定统用SVM方法基本依据

统用SVM评定多测点形位误差基本依据如下：

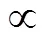
2）巧用核技术拓展应用SVM评定非线性形状误差。适当而灵活选定核函数可扩展应用SVM-R非线性回归方法评定各种形状误差。如，适当选定二次型核可用于圆度、抛物面等二次型形状误差评定[7]，可见巧用核技术有利于解决多测点空间形状误差评定的难题。还需指出，对于复杂形状求得核函数本身就是个难题。

4）充分利用SVM方法自身特色[6-7]。基于有限数据下VC理论及按SRM原则进行实值函数估计方法。强调直接采用从特殊到特殊的转导型推理方法，采用对偶化二次凸规划，其解具有全局最优性，且最优解只取决于在边界上少数点构成的支持向量与形位误差MS原则的极值点一致，而与其他样本点无关，又具有稀疏性、鲁棒性等。

5）验证形位误差评定结果准确度。统用SVM评定多测点形位误差的结果应予验证，尤其验证其准确度历来就是难点。推荐利用基于MonteCarlo方法给定误差（尤应含系统误差）数据仿真验证方法。

可见，统用SVM评定形位误差既合乎MZ原则，又可发挥SVM方法全局优化等优异性，关键在于需拟定简捷算法与合适的核函数。

2.3　多测点形位误差统用SVM评定的算法

显然，核心算法为平面度的线性二分类SVM评定：平面度MZ评定要求包容实际平面的正和负2包容面间的法向距离最小，理想平面则居中位，如图1所示。

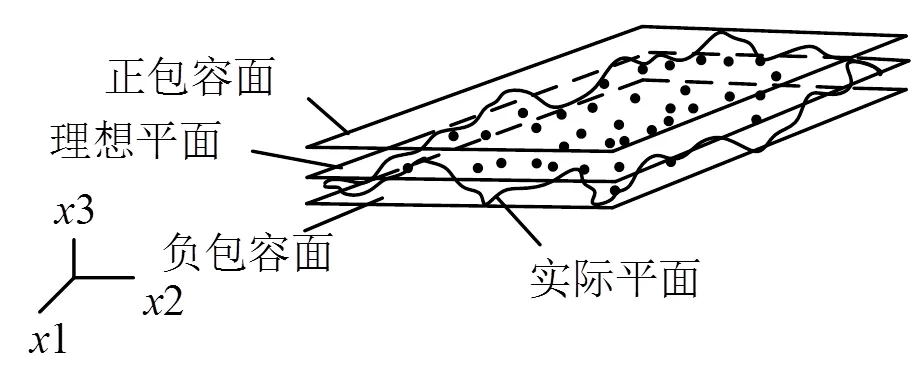
图1　平面度的线性二分类SVM评定

虽直接采用SVM-R即可评定，但为简捷起见，在文献[7]中用图2等价的正、负2包容面间最大间隔为最小线性二分类SVM-C分离式方法分离式支持向量分类（separating support vector classification,SSVC）来实现。该算法步骤：

1）减省数据点：SVM仅取决于支持向量数据点，即平面度多测点中的正和负MZ包容面上的数据点，而与其他数据点无关。为减省SVM算法数据点，先简捷地拟合与MZ平面接近的最小二乘（least squares, LS）平面，并移除约60%~70%小残差数据点。

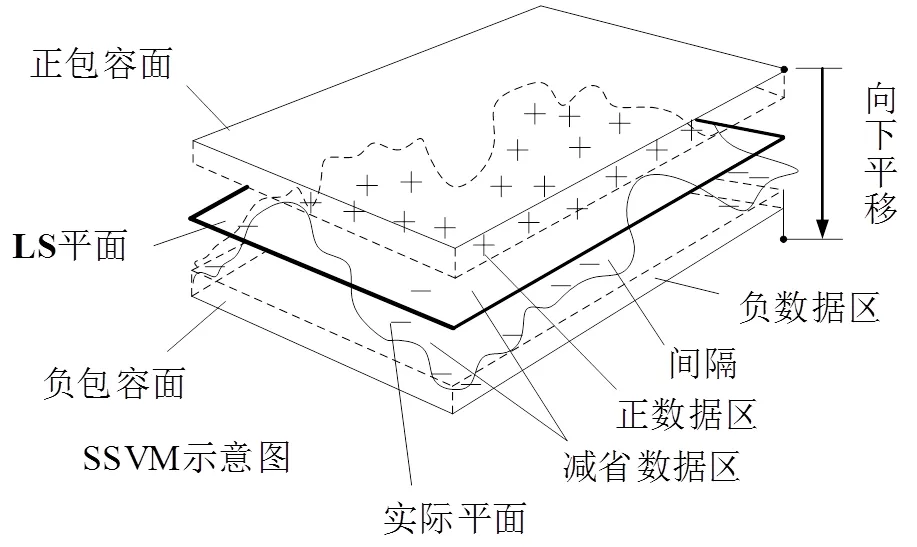
图2　最小线性二分类SVM-C分离式方法SSVC

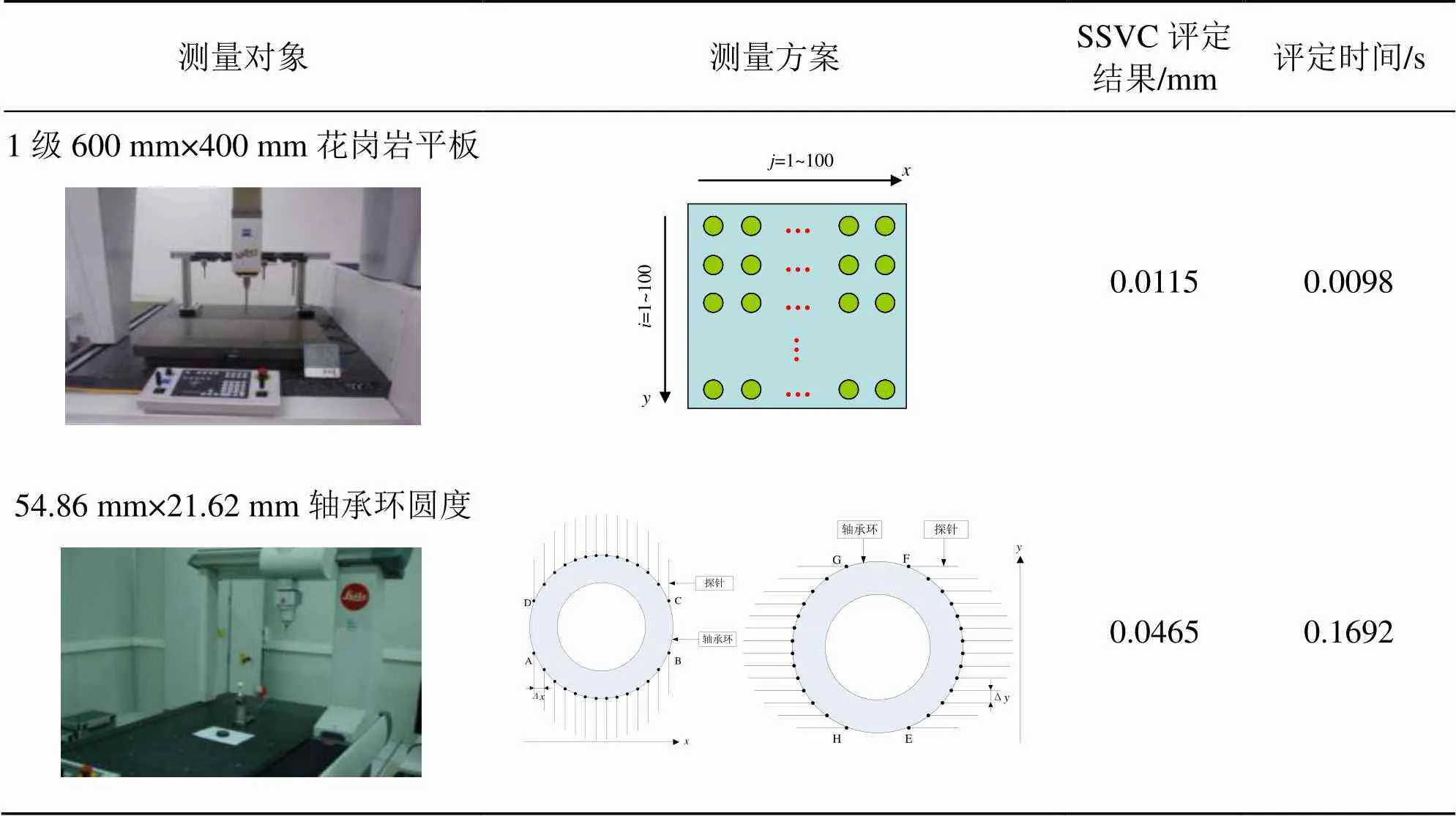
表1　测量示例

3　总结

在文献[1]述及，值得关注的总观念为：从特殊到特殊的转导推理该论文已具体化成SLT-SVM方法。现代数据处理对策四要诀：实、佳、智、验，在多测点形位误差评定的数据处理中也一一得以验证。

佳即应遵从最佳性原则。国内与国际标准均规定评定形位误差按MZ原则。SVM在数据处理的最佳性原则上恰为minmax准则，与MZ原则完全一致。

智即处理方法智能化。尽管使用LibSVM软件的SVM-R方法可直接用于评定多测点形位误差，这里力求创新更加简捷的智能化数据处理方法——SSVS算法。

验即处理结果准确性应予验证。对于以上所研究的具有创新性的结果更有验证之必要。在文献[1]所列举的恰为平面度测量验证性示例，只不过所述的是一般情况（免予重复）。实用中就需细致分析现实被测平面实际测量状况，拟定出合适的给定误差的数据仿真验证模型。

注意事项：拟定的验证模型项数、幂次等未必整、全，需经分析按实况而定；拟定的尺寸范围应与现实对象（即被测平面）的实物一致；拟定的误差大小与样本数据或数据图的变动波度相符合；系统误差设置宜有据：经验资料、专家意见等先验信息；随机误差分布设定应基于非高斯性为常态，即分布统示法。在文献[7]中有关平面度测量的给定误差数据仿真验证模型分析示例值得参考。最后，对仿真结果可做出仿真图形与原数据图对比以判别其适合性。总之，力求实而简。

[1] 林洪桦.测量误差分析及数据处理若干要点系列论文（一）——现代数据处理基本观念与四字要诀[J].自动化与信息工程,2020,41(1):1-4,9.

[2] 林洪桦.测量误差分析及数据处理若干要点系列论文（二）——随机性分布统示法综论[J].自动化与信息工程,2020, 41(2):1-7.

[3] 林洪桦.测量误差分析及数据处理若干要点系列论文（三）——随机性分布统示法推荐应用[J].自动化与信息工程,2020,41(3):1-7.

[4] Vladimir N.Vapnik.统计学习理论的本质[M].张学工,译.北京:清华大学出版社,2000.

[5] 邓乃扬,田英杰.支持向量机:理论算法与拓展[M].北京:科学出版社,2009.

[6] 林洪桦.测量误差与不确定度评估[M].北京:机械工业出版社,2010.

[7] 姜焰鸣.多测点平面度误差智能评定与不确定度分析方法研究[D].广州:华南理工大学,2012.

[8] 杨晓伟,郝志峰.支持向量机的算法设计与分析[M].北京:科学出版社, 2013.

Some Key Points of Measurement Error Analysis and Data Processing Series Papers (4)——Statistical Learning Theory and Support Vector Machine Method Used for the Evaluation of the Shape and Position Errors

Lin Honghua

(Beijing Institute of Technology, Beijing 100081, China)

This paper expounds the statistical learning theory and the support vector machine method used for the evaluation of the shape and position errors. First of all, the SLT-SVM method and its characteristics are sketched; then, the key points and difficulties of the shape and position errors evaluation for multiple measurement points are detailed described, as well as the basis and the evaluation algorithms of the unified SVM method; finally, the four key points of modern data processing countermeasures are verified: real, good, intelligent and empirical.

data processing; mathematical model; error; uniform expression method

林洪桦，男，1932年生，教授，主要研究方向：测试误差分析及数据处理。

TP274

A

1674-2605(2020)04-0001-05

10.3969/j.issn.1674-2605.2020.04.001