微织构摩擦副对微颗粒的输送特性研究

王传礼，薛朝文，何 涛，陈国瑜，李 成

(1.安徽理工大学机械工程学院，安徽 淮南 232001；2.中国矿业大学江苏省矿山机电装备重点实验室，江苏 徐州 221116；3.安徽理工大学矿山智能装备与技术安徽省重点实验室，安徽 淮南 232001)

研究人员从自然界非光滑表面得到启发，发现仿生织构对摩擦副的减磨特性有着重要的影响。微织构是指在摩擦副表面加工出规则分布的凸峰和凹谷形貌。表面微织构因其独特的纹理结构减小了摩擦副表面间的实际接触面积，使其具有存储润滑剂及磨粒,减小磨粒磨损、降低摩擦的重要功能[1-4]。煤矿井下微颗粒不仅影响采煤运煤机械性能，而且会损害设备安全。研究微织构阵列摩擦副对颗粒的自清理输送特性有利于提高设备的安全性能和使用寿命，但运动参数(频率、振幅)和颗粒大小对颗粒清理输送能力影响规律不明确[5-8]，使得煤矿水液压元件上微织构的应用仍处于试验阶段，加之织构尺寸较小直接研究难度较大，因此，目前针对织构自清理输送能力的研究也相对较少。为此需要通过相似理论放大模型参数，然后再基于EDEM对颗粒输送过程进行可视化仿真计算，在此基础上借助概率统计，对输送机理的影响因素进行对比分析与方差分析[9-12]，为煤矿机械设备关键摩擦副的微织构减磨机理研究奠定研究基础。

1 相似理论

1.1 力学模型

颗粒应力应变与相互作用力如图1所示，相互作用力F可表示为

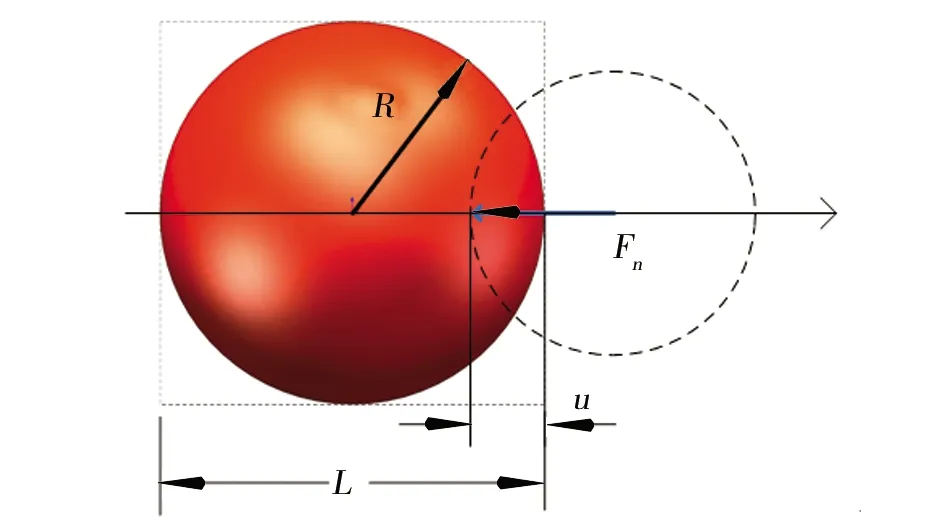
图1 颗粒接触几何特征图

F=F(u,R)

(1)

式中：u是两者的重叠/分离/滑动距离，R代表粒子(磨粒)的长度尺度，假设F为法向接触力，颗粒是球形的(结论也适用于其他形状)颗粒半径为R，则特征长度L，特征面积A，特征体积V分别是

L=2R,A=L2,V=A·L=L3

(2)

颗粒法向应力σ与应变ε

(3)

用粒子应力-应变形式等效地表达相互作用规律

σ=σ(ε,R)

(4)

则系统的能量E可表示为

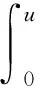
(5)

颗粒应变能密度函数可以定义为

(6)

1.2 几何相似

比例模型必须在几何上精确地表示物理问题，即严格遵守经典的几何相似性原则[13-14]。这两个模型的物理条件是按比例缩放的，应该具有相似的结构，并且只有一个恒定的比例因子，两个模型中的颗粒大小和域是不同的。设尺度因子为h,Rp和Rm分别为物理模型和放大模型中任意粒子的半径，Dp和Dm分别表示两种模型中域的特征长度。那么几何相似原理要求

(7)

1.3 牛顿力学相似

考虑物理模型中半径为Rp的任意颗粒，根据牛顿第二定律，任一自由面方向(法向、切向、径向)上运动方程可表示为

(8)

(9)

Fp(up,Rp)=Qp,Fp(up,Rp)δup=Qp(t)δup

(10)

根据(2)式，与颗粒相关的代表长度、面积和体积分别为

(11)

则颗粒应变、应力和应变能密度分别定义为

(12)

up=εpLp,Fp(up,Rp)=σpAp

(13)

式(10)可以分别用粒子应变、应力和应变能密度表示为

σp(up,Rp)=qp,δep(εp,Rp)=δwp(εp)

(14)

(15)

相似地，半径为Rm的相应粒子比例模型的控制方程可以表示为

σm(um,Rm)=qm,δem(εm,Rm)=δwm(εm)

(16)

式中：σm，um，em，εm分别为比例模型中颗粒应力，位移，能量密度，应变。力学相似要求颗粒应力、应变、应变能函数在两个模型中都有相同的，即

εp=εm,σp(εp,Rp)=σm(εm,Rm)

(17)

且wp=wm,qp=qm，能量密度相等在处理复杂的接触情况时是有益的。即

(18)

通过结合几何相似条件，可以得出

(19)

1.4 动力相似

当不能忽略粒子的惯性力时，必须满足附加条件，以确保可以按比例缩小在放大模型中获得的结果，从而获得物理模型的结果。以下将根据动态相似性原则建立所有必要条件，遵循流体力学的传统处理方法[15-16]，动力相似性的定义是作用在物理模型和比例模型中的所有力(惯性，内部和外部)都应具有相同的比率。因此，关于颗粒的动力学方程式(8)，动力学相似性原理要求

(20)

由准静态情况下得到的力学相似条件

(21)

则可得到

(22)

可推出

(23)

因此，在一般动态情况下，确保物理模型和比例模型精确等效的条件可以总结为

(24)

2 仿真模型

2.1 结构模型

建立的结构模型如图2所示，为模拟实际颗粒进入微织构摩擦副，在左上方设置颗粒工厂，且颗粒生成的位置、尺寸及速度均在设定范围内随机生成，并由输送机构把颗粒输送到右边的微织构摩擦副，右上方为摩擦副壁面，设置输送带以一定的速度使颗粒进入微织构摩擦副，在出口处设置Grid Bin Group虚拟几何体实时检测虚拟集合体中颗粒输送数目，及通过几何体出口颗粒总数。竖直方向为重力方向，垂直于输送方向的微织构两侧设置为周期性边界，消除边界效应。并通过量纲分析推导原型与模型参数如表1所示。

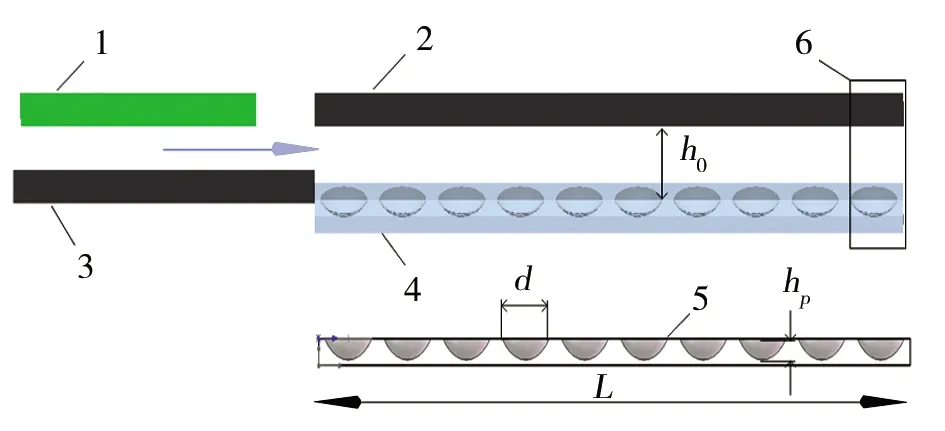
1.颗粒工厂 2.摩擦副壁面 3.输送机构 4.微织构摩擦副 5.微织构摩擦副剖面图 6.虚拟几何体图2 微织构摩擦副颗粒输送模型

表1 原型与模型参数

2.2 参数设置

EDEM仿真时间设置为120s， 颗粒总数为6 000个，生成速率为100个/s，R为2.5×10-3mm。Rayleigh Time Step取10%～20%，保存间隔0.01s。选择Hertz-Mindlin基础接触模型，颗粒及摩擦副材料参数和接触系数设置如表2和表3所示。

表2 颗粒与微织构摩擦副物理参数

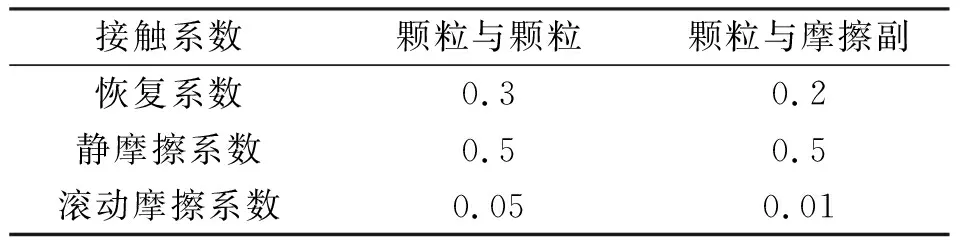
表3 碰撞特性参数

2.3 模拟过程

微织构摩擦副的微颗粒输送过程如图3所示，开始时(图3(a))。设置颗粒总数为6 000个，颗粒生成速率为100个/s，输送带速度为0.1m/s，设置微织构摩擦副为简谐振动，并对出口处虚拟几何体内的颗粒数进行统计分析，得到不同的频率、振幅、颗粒半径参数以及交互作用下的颗粒数目曲线。

图3 颗粒输送模拟过程图

3 仿真结果与分析

3.1 频率对微织构摩擦副颗粒输送的影响

为研究频率对微织构摩擦副颗粒输送的影响，分别设置微织构摩擦副的振动频率f=2Hz、3Hz、5Hz、10Hz、20Hz，设置振幅A=20mm，颗粒半径R=6mm。得到虚拟几何体中实时记录的颗粒数目如图4和图5所示。由图4可知，在开始阶段颗粒输送的曲线相似，颗粒进入微织构摩擦副快速达到稳定输送的最高值；t=20～80s的稳定阶段f=2Hz、f=3Hz、f=5Hz时Grid Bin Group中约120个颗粒，而f=10Hz时是76个，f=20Hz时颗粒数目为45，说明稳定输送时较低的频率具有较高的输送效率。图5斜率稳定说明微织构摩擦副具有稳定的输送能力；当t=80～120s时颗粒微织构颗粒数变少，低频曲线比高频曲线下降的更快，f=10Hz、f=20Hz时颗粒输送具有更高的稳定性。

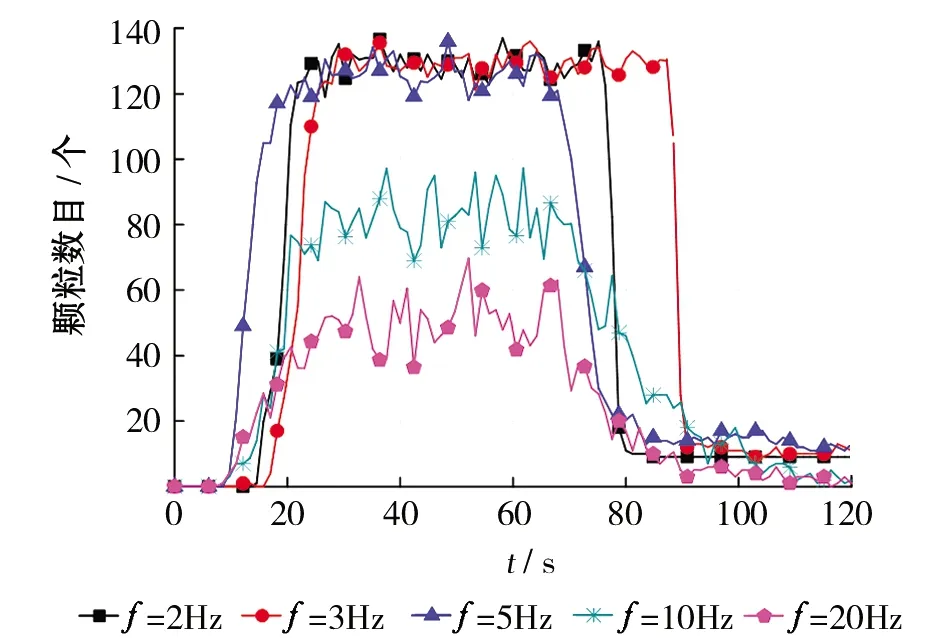
图4 频率对微织构摩擦副颗粒输送的影响

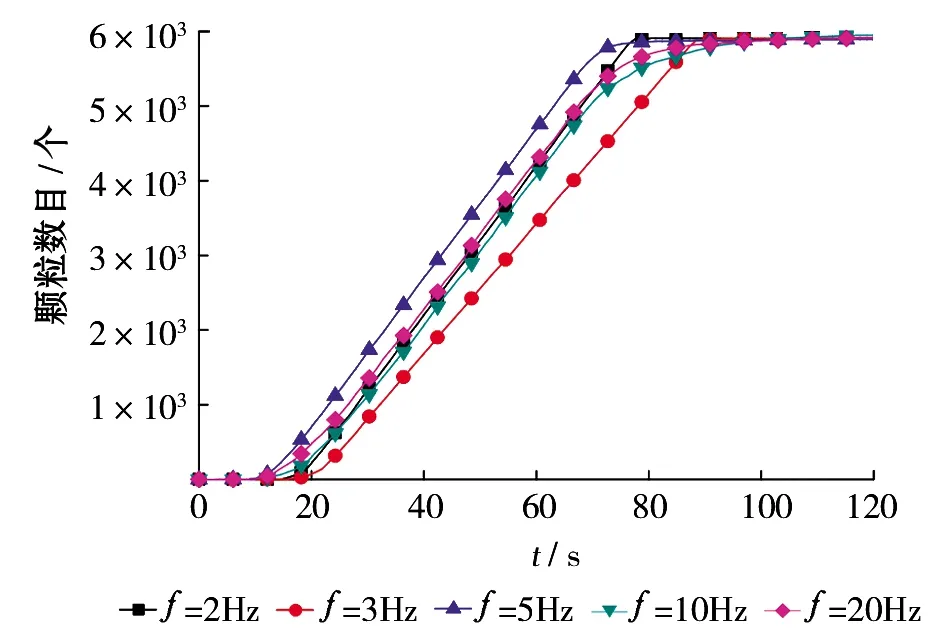
图5 频率对微织构摩擦副颗粒输送总数的影响

3.2 振幅对微织构摩擦副颗粒输送的影响

设置频率f=2Hz，颗粒半径R=6mm，研究简谐运动的振幅A=1mm、5mm、10mm、15mm、20mm时的输送特性如图6所示。当t=20s时颗粒进入微织构摩擦副达到输出的最高值，t=20～80s时可以发现不同的振幅曲线与输送均值几乎一致，t=80～120s时输送颗粒数目均值下降到10左右，进入缓慢输送阶段，这部分颗粒是微织构内储存一定量的微颗粒，微织构可以容纳微颗粒增加二次润滑减小微织构与壁面的直接摩擦。从图6得出在频率与颗粒大小相同条件下不同的振幅对微织构摩擦副颗粒输送几乎无影响。

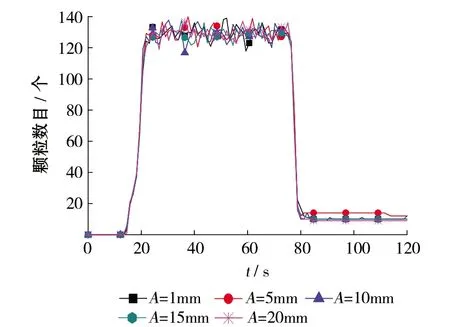
图6 微织构摩擦副振幅对颗粒输送的影响

3.3 颗粒半径对微织构摩擦副颗粒输送的影响

设置频率f=2Hz，振幅A=20mm，得到不同粒径颗粒的输送曲线如图7和图8所示，如图7所示，当t=20s时颗粒到达出口处进入颗粒稳定输送阶段，t=20～80s时，R=2mm、R=6mm、R=10mm、R=12mm、R=14mm颗粒输送均值分别约为130、120、60、35、28。结合图8各曲线斜率可知，随着颗粒半径的增大，输送效率逐步降低。t=80～120s时R=2mm、R=6mm、R=10mm的颗粒输送均值下降而R=12mm、R=14mm的输送均值保持不变，图8可以看出在相同时间内，粒径小的颗粒输送更多。

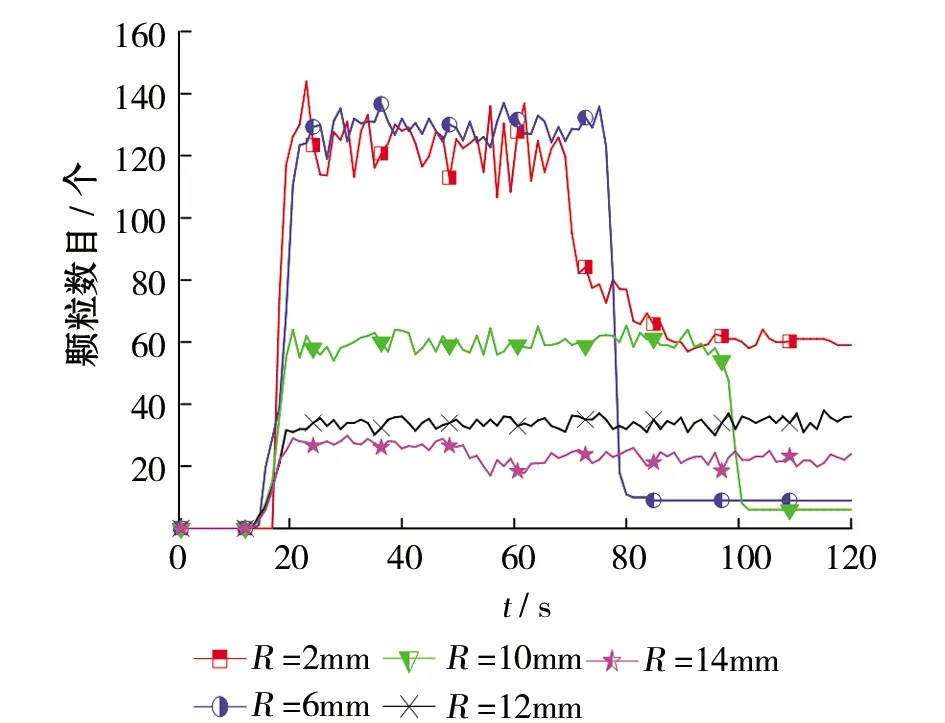
图7颗粒大小对微织构摩擦副颗粒输送的影响

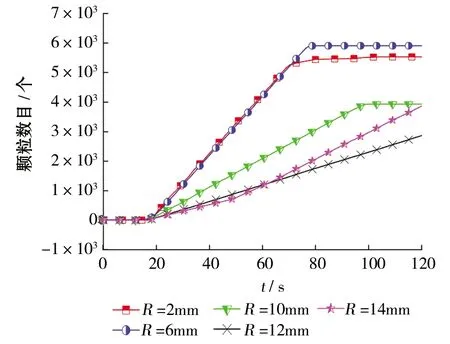
图8不同大小颗粒时微织构摩擦副输送总数曲线

3.4 交互作用分析

通过单因素的分析，发现一定范围内振幅对微织构摩擦副颗粒输送几乎无影响，做频率(A)与颗粒半径(B)的交互作用分析，找出最佳水平组合点，如表4所示。

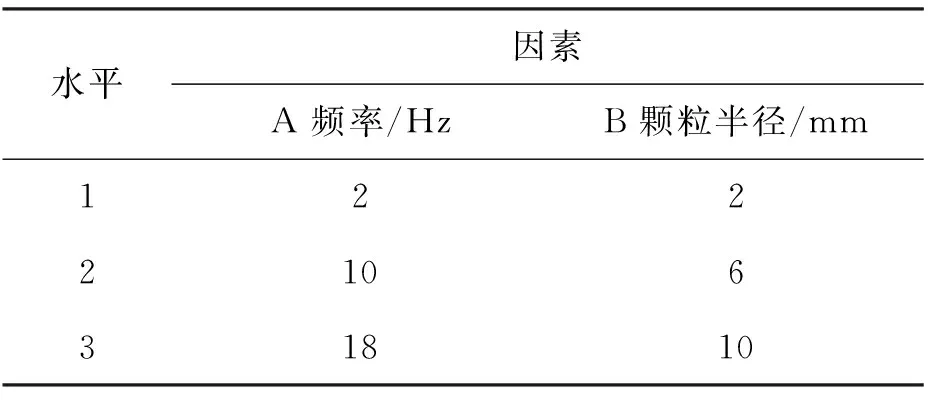
表4 因素水平表

图9 颗粒输送均值响应的主效应分析

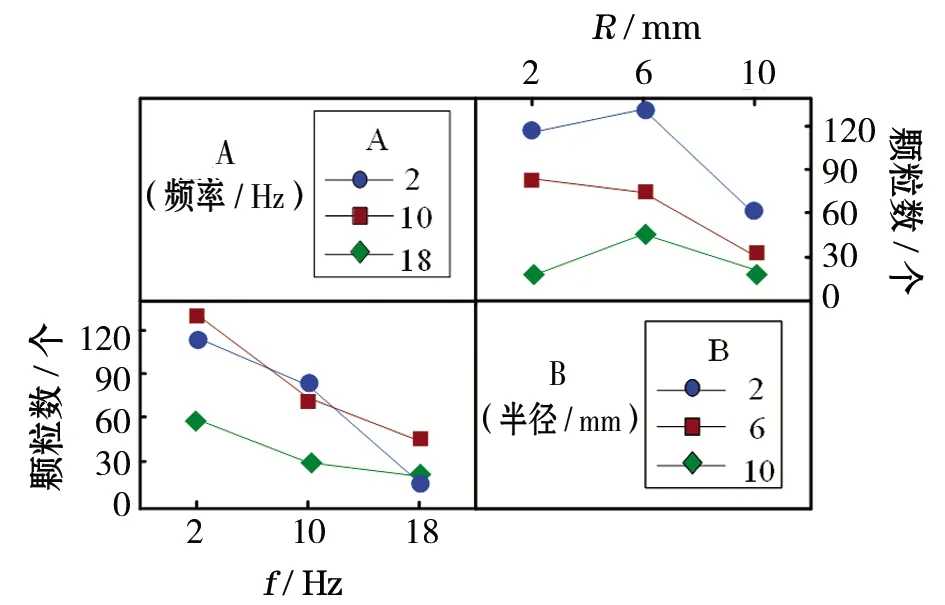
图10 颗粒输送的交互作用分析

由图9得到，影响颗粒输送均值响应显著性的因子A(频率)强于因子B(颗粒半径)，随着频率f的增大，颗粒输送均值增大，随着颗粒半径R的增大，均值响应曲线呈现先上涨后下落的趋势。当颗粒半径R=6mm时，输送均值较大，而频率f=2mm和f=10mm时输送均值较低。

由图10各列颗粒输送的交互作用可知，颗粒输送均值随因子的变化规律与图8基本相似。颗粒输送均值在A3B1，A3B3等交互的地方出现较小值，可见一般在B因子处于低水平或高水平，A因子高水平处，颗粒输送出现最小值的可能性比较大，输送效率较低的概率比较大。最优组合为A1B2，即频率为2Hz，半径为6mm时，输送均值最大，效率最高。

3.5 交互作用方差分析

对频率(A因素)，颗粒半径(B因素)和交互作用(AB因素)进行方差分析，稳定输送试验结果如表5和表6所示。

表5 试验设计与结果

通过分析交互试验数据, 得出方差分析表(见表6), 通过查表F0.05(2,9)=4.26，F0.05(4,9)=3.63，对于给定的显著性水平α=0.5可以得到频率的不同水平设置对颗粒输送影响显著，颗粒半径的不同水平设置对颗粒输送无显著影响，频率和颗粒半径的交互作用对颗粒输送影响显著。

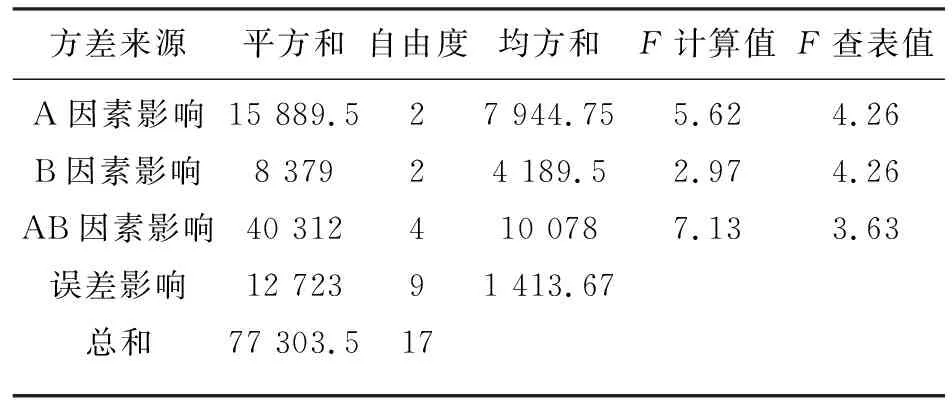
表6 方差分析表

计算各因素、 因素交互作用及误差对结果的影响

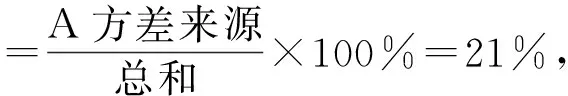
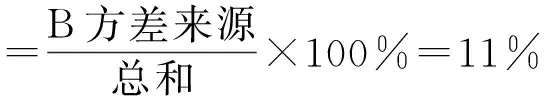
(25)

图11 A、B因素和交互作用以及残差占比率

4 结论

(1)仿真实验表明在输送颗粒时，微织构对微颗粒的容纳、捕获和输送作用减小了接触壁面间的摩擦，且微织构摩擦副对微磨粒具有较好的输送能和自清理能力。

(2)低频振动时微织构对微颗粒的输送效率更高，振幅对微织构摩擦副输送特性影响不大，当颗粒半径R>10mm时粒径越大，输送曲线斜率越小，输送效率越低。

(3)多因素交互作用下，频率(因子A)对颗粒输送均值响应的显著性强于颗粒半径(因子B)，颗粒输送均值随频率(B因子)的增大先增后减，且一般在B因子处于低水平或高水平，A因子处高水平时，输送效率较低。

(4)方差分析表明，颗粒半径对颗粒输送无显著影响，频率和颗粒半径的交互作用对颗粒输送影响显著，其中频率与颗粒半径交互作用对试验结果的影响占比最大(约52%)，其次为频率，最小为颗粒半径。