非均匀流重力排水管线计算机辅助设计选型
于一涵 于容朴 梁林海

摘 要:通过对污水站内非均匀流重力排水管线计算机建模,由上下游高差、管道长度、管道材质和管件数量几个参数,快速计算出最大设计充满度时所需的最小管道内径,对不同工况条件的运算结果进行了汇总,为工艺技术人員的设计选型提供了重要依据。
关键词:污水站;非均匀流;管线设计;计算机辅助设计
中图分类号:TV133.1文献标识码:A文章编号:1003-5168(2020)19-0076-03
Abstract: This paper built a model of the nonuniform flow in the gravity drainage pipe line with the drop head,the length, material of the pipe and the parameter of the pipe fittings .With the help of computer,we can get the smallest pipe type. This paper also summarized the solutions under different conditions, which provided the specialists an important reference when they design the system.
Keywords: sewage station;nonuniform flow;pipeline design;computer aided design(CAD)
污水站内的污水管线主要分为压力流和重力流两种形式,重力排水管线又分均匀流[1]和非均匀流两种形式。压力流管线的水力计算可按《室外给水设计规范》(GB 50013—2006)7.2.1条计算;室外均匀流重力排水管线可按《室外排水设计规范》(GB 50014—2006)4.2.4条选型;室内均匀流重力排水管线可按《建筑给水排水设计规范》(GB 50015—2019)4.4.7条计算,并满足最小坡度和最大充满度要求。工程中非均匀流重力排水管线的设计和选型尚没有充分的设计依据,因此这方面的设计成为工业污水站设计的重点和难点。
1 研究目的
水厂在做高程计算时,本着节能的原则,应尽量采用一次提升,利用重力流依次进入各处理单元[2]。大型市政污水厂一般单元较少、管线较粗、占地较大,不同单元之间的重力流管道布置比较顺畅,不同单元之间的重力流基本上符合等径、等坡、转弯缓慢、没有大阻力管件等条件,可作均匀流考虑,满足排水规范的充满度和坡度要求即可。对于小型工业污水站,情况恰好相反,单元多、管线细、占地不足。小型工业污水站的重力排水管线主要有细格栅、隔油、气浮、厌氧、水解、好氧、沉淀等单元的重力出水管线,当管线水平方向长度较大([L]≥20 m)且在连接过程中出现了水平和竖直方向的转向弯头、三通等管件时,管道中的充满度和流速发生较大变化,会出现气液两相流、阻力波动较大的情况,上述排水均为非均匀流重力排水管线。目前,在中小型工业污水站(日处理水量10 000 m3/d以下)调研中发现,因设计不当而造成非均匀流重力排水管道选型偏小的问题非常多见。
为避免出现上述问题,本文对此问题建立了数学模型,通过计算机给出了不同条件下的解并生成了快速选型表,为设计工作提供了设计依据。
2 计算模型的建立
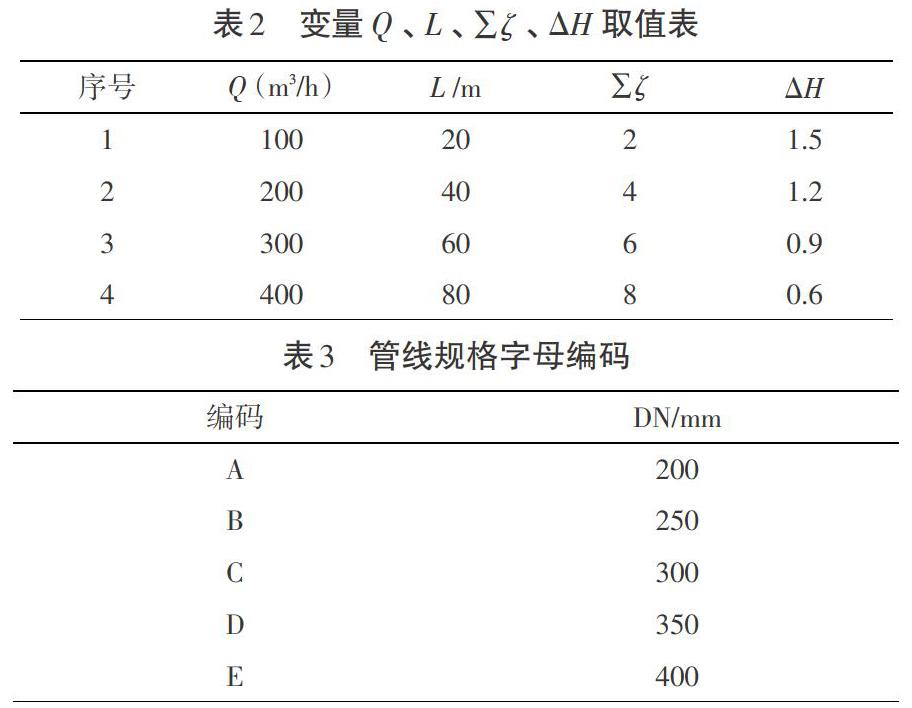
以某屠宰厂污水站预处理单元管线为例建立数学模型:站内采用运输车辆直接收集栅渣,细格栅采用架空设计。细格栅出水管相关标高:一楼地面相对标高0.3 m,顶部设栅渣斗,排渣口离地面3.5 m,渣斗高2 m,渣斗进料口与二楼楼板平齐,二楼楼板相对标高5.8 m;二楼细格栅的排水管管底超出二楼地面0.5 m,相对标高6.3 m,下游的隔油池顶标高为4.5 m,细格栅出水管线从隔油顶部进入,末端管底标高4.8 m。数学模型主要参数为:设计水量(提升泵最大流量)[Q]=300 m3/h;管道PE材质的粗糙系数[n]=0.009;细格栅出口至隔油池进口,管总长[L]=58 m;局部损失[∑ζ]=5.5(含弯头、三通、闸阀等);管径[Do]≥200 mm,充满度[h/Do]≥0.55;起始端液位高差[ΔH]=6.3-4.8=1.5 m;安全系数取[k]=1.25。
因管径、充满度、流速、坡度、局部阻力各参数间相互影响,传统算法需要试算,计算量较大。即使采用Excel软件,也需要多次试算,调整参数[3],易出错。在建模前先采用Excel反复计算数次得到最小内径为326 mm,取350 mm。
用计算机求解程序的流程控制如图1所示。
3 程序计算过程
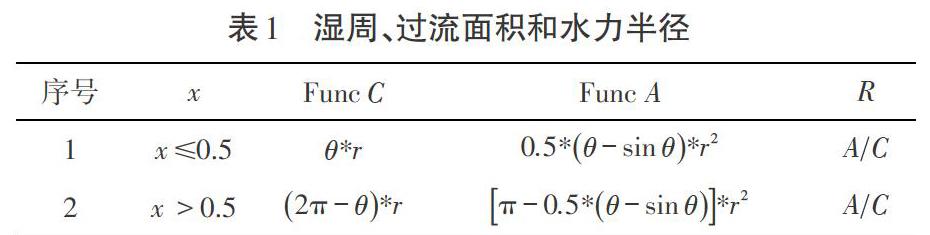
3.1 计算水力半径[R]
非充满条件下水力半径[R][4]的值等于过流面积[A]除以润湿周边[C],其关系如表1所示。
3.2 设计最大充满度与管道内径的关系
先初步确定设计管线内径为[Do],自定义充满度函数Func HvsD(x),Func HvsD为分段函数,不同管内径对应的最大设计充满度值按《室外排水设计规范》(GB 50014—2006)4.2.4条确定。
3.3 计算设计管道内径[D]
重力流排水横管采用谢才公式计算,已知[R]、[n]、[i]值,可求出实际条件下流速[Vs]。
当实际流速[Vs]≥理论最小流速[V]时,内径[D]值可满足运行要求。程序的计算模块算法采用循环语句,[D]值由初值DN200开始,以0.1 mm递增。管道的过流能力随着管道内径[D]的增加而增大,充满度也会阶梯性增加,管道的沿程损失会逐步减小,当管道总阻力损失满足高差要求[Ht]时,跳出循环语句。

