基于CAPM模型的个股适用性实证研究

陈 琪 冯 琴

(西南石油大学 四川 南充 637000)

一、CAPM模型理论研究

(一)理论发展脉络

Markowitz在“资产组合选择”的论文中，利用均值-方差体系，从数学层面分析得出通过投资组合可以降低投资风险的结论(Markowitz,1952)。他指出，在收益不变的假设下，理性投资者会选择风险水平较低的投资组合。这种研究方法为现代投资组合理论的研究开辟了道路。随后，不少文章在其理论基础上进行了一些修改。

1964年，威廉·夏普(Willian Sharp)在Markowitz证券组合理论基础上，引入了市场组合的概念，并对单种资产价格与风险关系这一问题进行了探索并取得重大突破。此外，Lintner(1965)、Mossin(1966)也分别佐证了威廉·夏普的结论。他们三人的研究结果构成了著名的CAPM模型(Capital Asset Pricing Model，CAPM)。这一模型的核心思想在于，风险资产的期望收益率与其系统性风险正相关，它第一次使人们可以对风险资产进行具体定价。

(二)CAPM模型的基本内容

CAPM模型基于一系列严格的假设前提，具体而言，包括市场完全竞争、所有资产可细分、投资者可以以无风险利率进行借贷任何额度的资产、在均值-方差体系下实现财富期望效用的最大化等条件。在上述严格假设前提下，该模型的基本形式为：

Ri=Rf+βi(Rm-Rf)

无论单个证券还是证券组合，其风险都可以用β系数来测定。将单个证券i换成任意证券组合P，则有RP=Rf+βP(Rm-Rf)，此时，证券组合的β系数是单个证券β系数加权平均，即：

β系数作为评判单个证券或证券组合的系统风险指标，其经济含义在于度量个股或特定资产组合对市场组合整体风险的贡献程度。其值的大小取决于该证券与整个证券市场的相关性、标准差和它自身的协方差。当市场组合相对于它自己的贝塔系数是1，如果一项资产的贝塔系数等于1.5，则说明这种资产报酬率的波动幅度为整个市场报酬率波动幅度的1.5倍。

二、CAPM模型适用性论证的样本选择

基于2015年1月1日至2019年12月31日(共计60个月)的数据，按月进行分析，利用Eviews7.2和Excel进行分析，得出股票的β系数和R2，即一般统计意义上的CAPM模型，并对其意义进行了说明。交易数据均来自同花顺网站和wind数据库。

(一)个股收益率的计算

本次实证在股票市场上随机选择了8只股票作为样本，它们分别为恒丰纸业(600356)、民生银行(600016)、中铁工业(600528)、北方稀土(600111)、中国人寿(601628)、老凤祥(600612)、新钢股份(600782)、长安汽车(000625)，其行业分布情况为造纸印刷业股、银行业股、制造业股、有色金属业股、保险业股、黄金股、钢铁股和汽车业股各有1只。股票为任意选择，且分布在多种行业，体现了科学的随机性并具有较好的代表性。

同时由万得数据库获得8只股票2015年1月至2019年12月每月的收盘价，根据公式求得股票其收益率为：

Ri=(本月收盘价格/上月收盘价格-1)*100%

(二)市场组合收益率的选择

本文的研究对象除了长安汽车(000625)以外，都是在上海证券交易所上市的公司，而上证综指指数以上海证券交易所挂牌上市的全部股票为成份股，它作为一种以发行量为权数的加权综合股价指数，正好能反映整个股市价格变动情况和走势，故选择上证综指指数作为市场组合指数，并用其收益率代表市场组合的收益率，其计算公式为：

Rm=(本月收盘上证综合指数/上月收盘上证综合指数-1)*100%

(三)无风险收益率的确定

无风险利率可以理解为投资者投资无风险资产可获得的期望报酬率。目前，我国政府债券基本没有违约风险。所以，结合研究周期，文中选取5年期的国债利率作为无风险利率的代表。统计其自2015年以来的利率及调整日期，按照加权平均的方式计算5年期国债年利率，最终，2015年1月1日至2019年12月31日的5年期国债利率加权平均数为4.5%，折合到月利率为0.375%。

三、CAPM模型实证分析

(一)模型设定

在实践中对于此模型的检验，通常涉及两次回归。

第一阶段回归即估计个股的β系数，本文用8只股票的月超额收益率Yit与上证综合指数的月超额收益率Rmt进行时间序列的回归，相应地定义了8个解释变量，通过建立一元线性OLS回归方程，从而得出这8支样本股票的β值，其回归模型如下:

Ri-Rf=αi+βi(Rm-Rf)+εi

同时进一步简化为：

Yit=αit+βitRmt+εit

其中，Yit表示股票i在t时间的月超额收益率，Rmt为上海证券综合指数m在t时间的月超额收益率，αit、βit为待估参数，εit为误差项。

第二阶段回归是在第一阶段回归模型确定β系数之后，将β值作为输入量与8只股票的月平均超额收益率再次进行回归，并进行相应的检验。

(二)回归分析

根据第一阶段的回归结果，估计出8只股票的β系数，所得结果如表1所示：

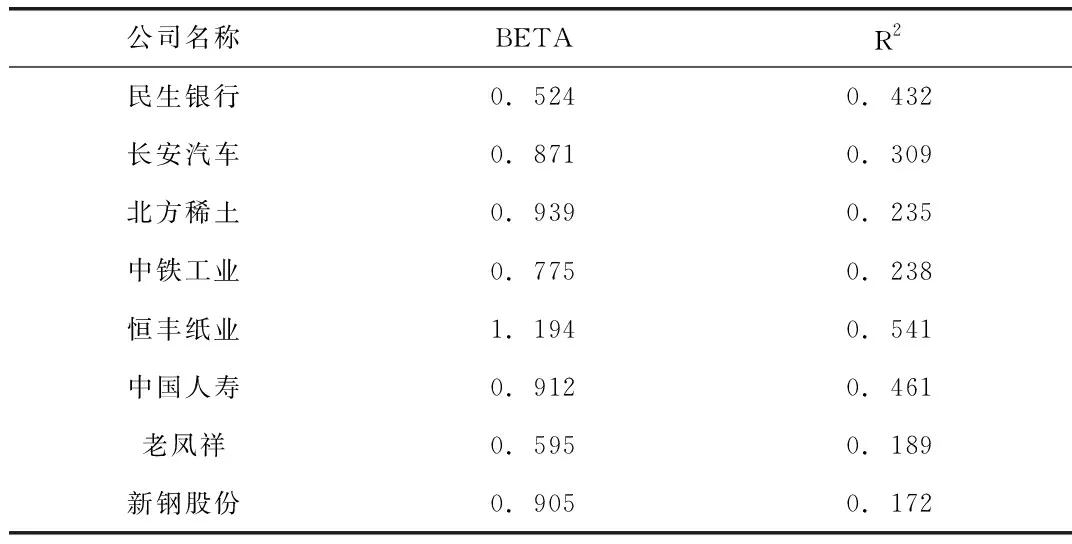
表1 回归结果描述性分析

由表1可知，β系数的估计值最大为1.194，最小为0.524，均值为0.840。7只股票系数小于1，说明当市场收益率上升或下降时，这些股票的上升或下降幅度会小于市场收益率变化幅度；1只股票(恒丰纸业)系数为1.194，说明当市场收益率每变动一个单位时，恒丰纸业收益率将变动1.194个单位，其价格波动与市场平均股价波动相当，属于中性型股票，相比于其他7只股票来说，其投资风险更大；此外，除了恒丰纸业，其它股票的可决系数均小于0.5，可决系数对个股超额收益率的变化中平均有32.211%可以用市场的超额收益率来解释，也就是说市场组合对个股的解释效果一般。此外，对β系数进行t、F检验所得结果均显著，且正态分布检验中Jarque-Bera=17.78803，Probability=0.000137，结合图形可看出其符合正态分布，多数β系数的估计值都在均值附近，通过上述结论可以推出根据第一阶段数据估计所得β系数基本是有效的。

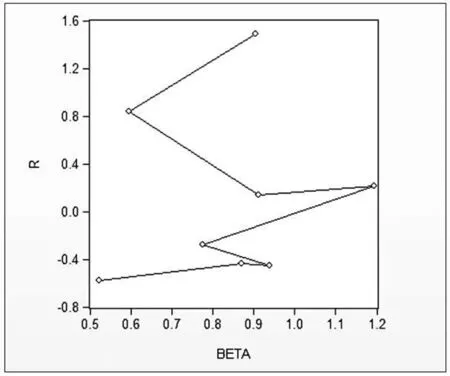
图1 月平均收益率与BATA散点

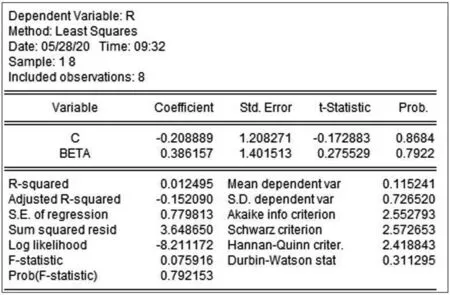
第二阶段将8只股票的贝塔系数，与其月超额平均收益率进行风险和收益的回归。首先，根据散点图(见图1)，可看出贝塔系数与股票风险溢价之间的线性关系不明显。进一步，用Eviews7.2软件进行回归得到表2，由表2书写结果：

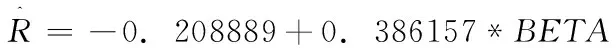
可知个股风险溢价的系数约为0.386，但拟合度很小，且β系数与个股股票风险溢价未通过T和F检验，其关系不显著。综合以上的分析，可得知从数据估计中所得β系数适用性不强，资本资产定价模型在本次样本研究中的适用性并不显著。

四、结论与展望

从研究结果来看，除了恒丰纸业外，其余股票相比市场组合风险而言，波动幅度明显较低。本文在某种程度上，说明个股收益率的变化与大盘指数关系不大。整体上看，所代表的市场风险并不能很好地解释个股风险溢价。那么，在此情况下，用CAPM模型来评判和预测股票表现，就有可能出现偏差。

由于CAPM模型基于一系列严格假设条件,使得实际股票市场与这些前提条件有一定差距,用某种股票价格指数代替市场收益率的方式，在一定程度上也对其使用效果产生了偏差。总体来说，虽然其经常被评价为不现实，但在实际的资本市场中，市场的预期回报与系统风险之间可能仍然存在一个比较强的线性关系。决策者在应用该模型时，如果能注意前提条件与现实经济的差距，并根据自身的情况去计算参数，相信可以为项目决策和风险管理提供一定的参考建议。