混凝土局部楼盖模态测试及FEM模拟分析

付章建， 岳祖润， 梁文彦

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043； 2.河北省建筑科学研究院有限公司，河北 石家庄 050021; 3.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001)

随着人类需求的多样化，人类对于建筑结构的要求已经远远不限于满足安全性、适用性、耐久性，而对于结构舒适性提出了越来越多的新要求，尤其是近20年，楼盖结构的舒适度问题已经引起了世界各国的广泛关注，如果楼盖结构振动问题控制不当，不仅会影响建筑居住者的身体健康，也会影响精密设备的正常工作和寿命，甚至会造成结构的破坏，目前，英美等国已经进行了大量的实测研究，颁布了多项版本的规程、指南[1-9]。为了满足结构对于舒适度的要求，我国也颁布了一系列的相关规程、指南[10-16]，采用结构竖向自振频率、竖向加速度峰值等评价指标进行结构舒适度评价。

本文通过实践和理论相结合的方式，首先通过模态测试获取所测试局部楼盖的动力特性，然后通过FEM进行模拟分析。通过FEM分析与现有结果比较，验证了本文测试方法和模拟结果的正确性与可靠性，该测试方法不仅可以应用于复杂结构的结构动力特性预估及优化设计，而且可以用于诊断和预报结构系统的故障，识别结构系统的载荷。

1 楼盖模态测试

1.1 工程概况

本次测试工程为河北省衡水市桃城区某小学体育馆，该结构为地上2层的混凝土框架结构，一层为梁板式楼盖，平面布置图如图1所示。

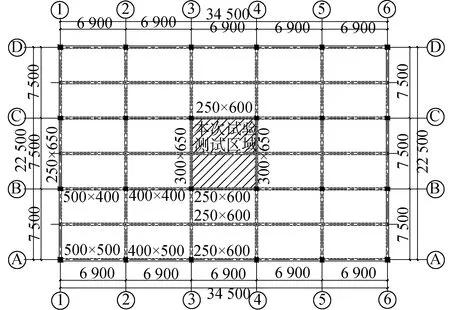
图1 一层楼盖平面布置Fig.1 The plane layout of the first floor

本次测试区域为阴影部分，测试区域横向跨度7 500 mm，纵向跨度6 900 mm，横向主梁截面尺寸为300 mm×650 mm，纵向主梁、次梁截面尺寸均为250 mm×600 mm，柱子截面尺寸均为400 mm×400 mm，楼板为现浇楼板，厚度为110 mm，结构梁、板、柱混凝土强度等级均为C30。

结构模态作为结构的一个重要特性，在处理结构振动问题时，必须对其动力特性有全面的了解，结构的动力特性通常用各阶模态参数(模态频率、模态振型和模态阻尼)描述，通过对结构的模态测试可以得到准确的动力特性参数，进而与理论计算结果进行校验。

本模态测试用到的仪器设备主要有：16通道东华(DHDAS-5921)动态信号采集分析系统一台、100 m的2×0.3RVVP 信号屏蔽线、东华2D001VDH610V加速度传感器及信号接收软件等。其中，加速度传感器灵敏度指标在(300～370 mV/(m·s-2))，可以满足对楼盖结构测试信号要求。现场测试图如图2所示。

图2 动力特性现场测试Fig.2 Field test of dynamic characteristics

1.2 测试原理

本测试采用自然激励技术法(natural excitation technique，NEXT)，通过计算出自然激励下实测信号的互功率谱，经过傅里叶变换得到结构测试各点与参考点之间的互相关函数，然后与时域识别方法特征系统实现算法(eigensystem realization algorithm，ERA)相结合进行模态参数识别。

设一个n个自由度的线性体系，其一般运动方程为：

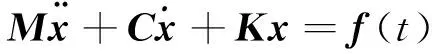
(1)

式中：M、C、K分别为质量矩阵、阻尼矩阵、刚度矩阵；x为位移；f(t)为激励力的列向量。

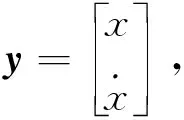
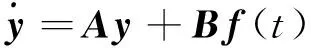
(2)

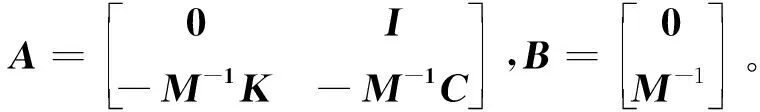
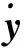
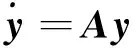
(3)

对于n自由度系统，A为2n×2n阶矩阵，由于A矩阵的上半部分由零和单位矩阵组成，故A矩阵的未知元素为n×2n=2n2个，方程适用于任何时刻ti。

因此，如果在n个坐标上对位移、速度、加速度进行测量，每一组采样y(i)可得到n个线性非奇次方程，如果在2n个不同瞬时进行采样，便可得到2n2个方程，即可确定n个未知量，则式(3)可以写成：

(4)

(5)

令方程的解为：

y=ψexp(λit)

(6)

式中：λ为A的特征根，代入式(5)可得：

λψ=Aψ

(7)

从式(7)可以看出，对模态参数的识别问题可转化为广义特征值问题。A矩阵的特征值可给出系统的自然频率、阻尼信息及其特征矢量，即模态矢量。

然而，欲进行时域识别，则需要对加速度、速度、位移信息同时进行测量，但在工程实践中这样做是不现实的，也是不需要的，对于n自由度的线性系统位移响应可表示为：

(8)

对式(8)进行2次微分，得到：

(9)

(10)

(11)

(12)

因此，只取得其中一种响应数据，便可得到系统特征矩阵A，本次测试选用加速度作为响应数据。

1.3 测试系统

本文采用的测试系统主要由4个部分构成：

1)激振部分，由于该结构不易获得激励力，且环境激励下不会影响结构的正常工作，更加符合实际工作状态，因此，本测试采用环境激励作为激振振源。

2)拾振部分，本测试采用拾振部分为接触式的测量设备——压电晶体式加速度传感器，二次仪表采用电压放大器。

3)数据采集及谱分析部分，将测试所得到的响应信号传递到计算机上，对其进行FFT变换的谱分析及传递函数分析。

4)曲线拟合及模态参数识别部分，采用计算机通过自互功率谱的方式进行模态识别。

这4个部分协调工作，从而完成测试。

1.4 测点布置

根据《建筑工程容许振动标准(GB 50868-2013)[16]的要求，结构板构件可视为连续弹性体，理论上具有无穷振型。在振动过程中各点的振幅不同，具有随机性，因此测试中采用多点测试统计平均方法。

此外，振动测试方向应与结构楼板的垂直方向(法向)一致，同一构件上的测试点应等间隔均匀布置。对于板构件的振动测试，测点数量不应少于5个。本测试对象为一层局部楼盖3～4×B～C，采用35个测点进行测试，以期得到良好的测试效果，拾振器参数设置如表1所示，测点布置如图3所示。

图3 测点布置Fig.3 The plane layout of the test point

表1 拾振器参数设置(采样频率100 Hz,电压测量)Table 1 Parameter setting of vibration picker (sampling frequency 100 Hz, voltage measurement)

1.5 实测过程

由于本测试采用环境激励的方式进行，为减少信号干扰，所以测试时间选择在晚上进行。通过单点拾振获取各测点的振动加速度，为了提高测试效率与准确性，本次测试共采用13个拾振器，整个测试过程中，A18传感器不动，其余传感器测试完一组数据后进行移动，传感器布置图如图4所示。通过3组测试完成了所测楼盖的模态测试，所测得的加速度时程曲线如图5所示。每组测试时间为25 min，数据采集频率为100 Hz，采集完成后通过自互功率谱的方式进行模态识别，确定模态参数。

图4 传感器布置Fig.4 Layout of sensors

图5 7号测点加速度时程曲线Fig.5 Acceleration time history curve for measuring point 7

1.6 测试结果

采用自互功率谱对现场实测数据进行模态参数的识别以及振型的识别，计算分析得到该结构一层局部楼盖3～4×B～C的一阶、二阶模态振型如图6所示，振动频率和阻尼比如表2所示。

2.3.2 疾病经济风险度:由表5可知，门诊自付费用给低收入组和中低收入组的患者带来了很大的风险(矫正RR值>1)，比如，低收入组门诊就诊经济风险度约是高收入组的18倍。随着收入水平的增加，患者门诊就诊的经济风险也逐渐缓解。

表2 楼盖频率和阻尼比测试结果Table 2 Test results of floor frequency and damping ratio

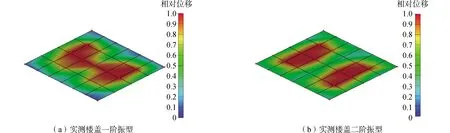
图6 实测楼盖振型Fig.6 Vibration mode of measured floor

2 楼盖模态FEM模拟

通过采用有限元方法对楼盖模态进行模拟计算，与试验结果进行校核，从而判定建立有限元模型时所引入的一系列人为假设与实际情况是否相符，结构的动力特性是否符合要求，进而应用于进一步的动力特性研究。

2.1 有限元模型的建立

为了准确模拟楼盖结构的振动特性，本次分析采用整体建模的方式，尽可能的模拟实际工作状态，以充分考虑局部楼盖周边构件的约束作用。采用ANSYS软件进行三维建模，BEAM4 单元模拟柱单元，BEAM189单元模拟梁单元，SHELL63单元模拟板单元，采用映射网格划分六面体单元，得到有限元模型如图7所示。

图7 ANSYS模型Fig.7 The model of ANSYS

2.2 参数选取

为了准确模拟结构的动力特性，取混凝土密度为2 500 kg/m3，弹性模量为3.0×1010Pa，泊松比为0.2，混凝土板的阻尼取为0.05，本次有限元模态分析方法采用 Block Lanczos 模态分析方法，该法适用于大型有限元模型模态分析，并采用PCG求解器，得到了如图8所示的一阶、二阶模态振型。

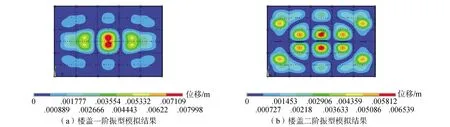
图8 楼盖振型模拟结果Fig.8 Simulation results of floor vibration mode

3 结果对比分析

本文对数值分析结果与实测结果进行对比，如表3所示，可以看出有限元数值分析得到的模态参数与实测数据识别的模态参数结果拟合良好，最大偏差仅为5.9%，足以满足工程分析的精度要求，从而验证了本文模态测试方法的正确性。

表3 2种方法结果对比Table 3 Comparison of the results of two methods

通过对有限元结果与实测结果的进一步分析，可以得出以下结论：

1)由于所测楼盖为局部楼盖，只有当结构的模态较高时，才会表现出局部楼板的振动，因此，需要在高阶模态中准确寻找所测楼板的振型及频率。

2)2种方法得到的一阶、二阶振型图基本吻合，且振动频率均在14.5 Hz左右，一层楼盖3～4×B～C会出现显著的振动。最大振幅达到8 mm，说明 14.5 Hz 为该楼板的敏感振动频率，当外界振动接近该频率附近时极易引发结构的共振。

3) 本次动力测试的实测结果与所建立有限元模型动力特性较为相近，足以说明该模型可以用于进一步的结构动力分析与研究。

4 结论

1)通过现场实测和有限元模拟结果得到的局部楼盖振型图及振动频率对比，验证了本文测试方法正确性及模拟结果可靠性。

2)采用环境激励下的振动响应数据进行模态参数识别对于复杂环境下大型结构模态测试是一种行之有效的方法，而且更加符合实际情况和边界条件。

为准确得到局部楼盖振动特性，建议采用整体建模方式，以充分考虑楼盖结构周边构件约束作用，获得可靠的模拟结果，利于开展进一步的动力分析和研究。

在环境激励下，由于高阶模态无法被激发出，因此，对于高阶模态的识别需要进一步研究。同时，如何将子结构综合成整体结构进行分析也是下一步研究的重点。