用Excel求二元非理想体系精馏塔理论塔板数通用方法分析研究

王菁 杨智勇

摘      要：介绍了用Excel计算和图表功能，是对二元非理想体系进行逐板计算法和图解法相结合求精馏塔理论塔板数的一种新方法。对方法中的关键问题如曲线拟合和单变量求解等进行了具体分析和说明。计算方法简单实用，无须编程。经实例验证结果准确，具有实用性和一般性。

关  键  词：精馏塔;理论塔板数;逐板计算法;图解法;非理想体系

中图分类号：TQ028.1     文献标识码： A       文章编号： 1671-0460（2020）04-0704-07

Abstract： A new method for calculating the theoretical number of distillation columns in a binary non-ideal system by combining the plate-by-plate method and the graphic method with the Excel calculation and chart functions was introduced. The key problems in the method， such as curve fitting and univariate solving， were specifically analyzed and explained. The calculation method is simple and practical. The results of the examples have verified the accuracy， practicality and generality of the method.

Key words： Rectification tower; Theoretical plate number; Plate-by-plate calculation method; Graphical method; Non-ideal system

化工原理是过程工程类专业（包括化工、制药、轻化工程等）的一门专业基础课程和主干核心课程[1]。精馏是化工原理中最重要的传质分离单元操作之一，也是化工生产中最普遍使用的分离工艺过程。主要用于液体均相混合物的高纯度分离。具有概念多、公式多、计算过程复杂、工程概念强等特点。对培养学生运用理论知识解决实际工程问题的能力有重要作用。尽管目前分离液体混合物的新技术、新方法层出不穷。精馏过程仍是其最重要的手段，精馏理论、精馏塔的优化设计和迅速、准确、可靠地自动控制等问题仍然是化学工程领域研究的重点，也是化工原理教学中的重点和难点。

对精馏过程进行设计或操作计算，精馏塔理论塔板数的计算都十分重要[2]。

在传统的教材[3-6]中，若物系符合恒摩尔流假定，操作线为直线，可用图解法或逐板计算法求取理论板数及理论加料位置，如用图解法，为了得到较准确的结果，应采取适当比例的图。当分离要求较高时，应将平衡线的两端局部放大，以减小作图误差。当分离物系的相对挥发度较小，或分离要求较高，操作线和平衡线就比较接近，所需的理论板数就较多。若用图解法不易得到准确的结果，应用逐板计算法进行计算。在此种情况下应特别注意相平衡数据的精度，数据的微小差别也会造成理论板数的很大误差。对于非恒摩尔流物系，求取精馏塔理论塔板数，需用焓浓图进行求解。逐板计算法可以得到每一块理论塔板上的气液组成，为精馏塔的设计和控制提供准确、详细的数据依据;计算结果准确度高，且能确定理论塔板数和加料板位置[7]。但手工逐板计算过程繁琐，工作量大且复杂，容易出错，操作十分不便。而且条件一旦改变，就只能重新计算。理论塔板数的求解法也可运用图解法，此法非常简单、直观，但当塔板数较多时，计算结果误差较大且不易准确[6]。虽然图解法非常直观、简便，但当理论塔板数较多时，图解则不易准确，误差较大，而且图解法提供的数据结果十分有限。手工图解法准确性较差，采用手工计算只能解决小规模问题，难以达到较好的教学效果。

随着计算和信息技术的发展，精馏计算已经摆脱了手工计算、图解方法。许多研究者采用不同的计算机软件进行精馏的计算、图解研究。涉及逐板计算法的有从最初使用的Fortran[8]到Basic[9]、C++[10]、MathCAD[11]、MATLAB[1]、Mathematica[12]、Maple[13]、VB[6]、等，其中计算周期长、程序庞大、运行结果不直观都是使用计算机程序存在的问题[1]。

涉及图解法计算精馏塔理论塔板数的方法有：使用AutoCAD[14]、MATLAB[15]、Excel[2]、origin[16]以及自行设计软件等，大多只能进行理想体系的图解，只能得到较少的理论板数的信息，很少有将逐板和图解两者结合，既保留图解法的直观效果，可以在图中查出每块塔板上气液相的组成，又可直觀的找到加料板位置和理论塔板数[17]。

1  原理和步骤

1.1  有关方程

在精馏塔计算中，对于设计型计算，需要气液相平衡关系图，其图的准确性直接影响设计结果。一般情况下需在物性手册里，查出某一温度t下轻组分和重组分的饱和蒸汽压，根据安托因公式算出气液相组成，通过描点法得出气液相关系图。因此对非理想物系不论是逐板计算法还是图解法，都必须首先得到气液相平衡关系的具体的函数表达式即相平衡方程。

最好利用专门的非线性方程求解数值进行计算来解决这一问题，Excel中内嵌入的非线性方程求解的方法收敛迅速，但对初值要求较高。在单变量求解功能中给出。

1.3  图解法求理论板数的过程

逐板计算气液相组成可以在Excel工作表中完成，然后把计算结果，列入Excel中，用其图表功能完成制图。平衡线、操作线和阶梯是图解法求精馏塔理论板数到多步绘图的关键[1]，图表曲线有6个系列，分别为x-y气液平衡线、对角线、精馏段操作线、提馏段操作线、q线和表示塔板的梯级线。在利用Excel进行非理想体系的精馏理论板数的求解过程，实际上是图解过程和逐板计算过程交替进行，相互依赖。下面以乙醇-水混合液精馏过程理论板数计算和图解为例进行具体说明。

设计任务或主要技术指标：在一常压操作的连续精馏塔内分离乙醇-水混合液。年产0.8万t，组成为40%（乙醇的摩尔分数，以下同），要求塔顶馏出液的组成为0.94，乙醇回收率为99%。进料温度为30 ℃。操作压力（塔顶常压），进料热状况泡点进料，回流比自选。

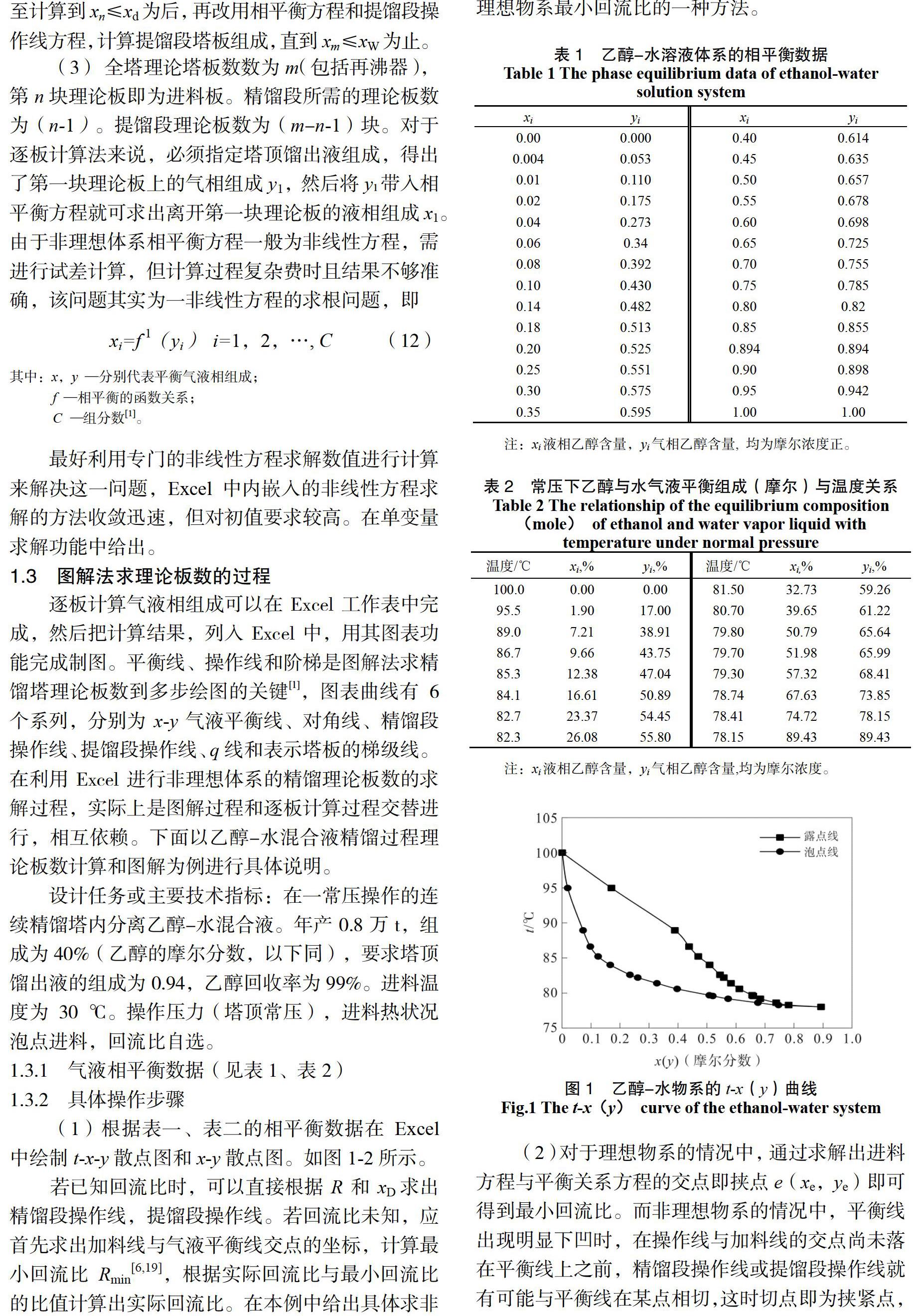
1.3.1  气液相平衡数据（见表1、表2）

1.3.2  具体操作步骤

（1）根据表一、表二的相平衡数据在Excel中绘制t-x-y散点图和x-y散点图。如图1-2所示。

若已知回流比时，可以直接根据R和xD求出精馏段操作线，提馏段操作线。若回流比未知，应首先求出加料线与气液平衡线交点的坐标，计算最小回流比Rmin[6，19]，根据实际回流比与最小回流比的比值计算出实际回流比。在本例中给出具体求非理想物系最小回流比的一种方法。

（2）对于理想物系的情况中，通过求解出进料方程与平衡关系方程的交点即挟点e（xe，ye）即可得到最小回流比。而非理想物系的情况中，平衡线出现明显下凹时，在操作线与加料线的交点尚未落在平衡线上之前，精馏段操作线或提馏段操作线就有可能与平衡线在某点相切，这时切点即为挟紧点，其对应的回流比即为最小回流比Rmin。

因而，对于非理想物系求解最回流比，关键是找出挟紧点e（xe，ye）坐标[20]。在本例中，挟点在精馏段操作线与平衡线的切点上。求最小回流比Rmin的方法是在x-y图上，过点（0.894，0.894）做相平衡曲线的切线，与y轴的交点为（0，0.210 85），则

如前所述方法逐板计算。由于相平衡曲线拟合为6次的多项式，由气相组成计算液相平衡组成实际是解6次的非线性方程问题。该问题的难点在于初值的选择很重要，否则很难收敛。许多研究者在编程解决此问题时，一般选择一元三点插值多项式或选择分段函数进行曲线拟合的方式，使最高幂次降低到3次。由于已有了相平衡的实验点，对于气液相组成我们已可以在较窄的区间范围进行试差，使用Excel的单变量求解功能计算液相平衡组成。

a）在Excel中新建一个工作簿，在sheet1（工作表）中输入表1乙醇-水气液相平衡组成如A、B列数据所示，在C列列出对角线数据。D、E、F列分别输入精馏段、提馏段、拟合的6次多项式气液平衡方程，利用Excel填充柄功能可以快速完成此三条线的相关计算，为逐板计算和图解理论板奠定基础。具体结果如图3所示的工作表格截图。

b）以A、B列数据为基础，在Excel菜单“插入”中选择“图表”中的散点图如图3（a）所示，选择“带光滑曲线和数据标记的散点图”（b）所示，做如图3所示的气液相平衡图，在图中右键点击气相线，选择“设置趋势线格式”图（c）所示，拟合出图4所示的乙醇-水非理想体系气液相平衡函数关系式。在此基础上，在散点图中点击右键选择“选择数据”出现“选择数据源”对话框，如图d所示，按此操作即可在图4上做出对角线。

将图2中数据作图得x-y曲线。在Excel中点击该曲线选择添加趋势线，选择多项式，当多项式次数选择为6次时，拟合效果最好。该曲线拟合成下式表达：

y = -68.592x6+208.22x5-248.12x4+147.6x3

-45.865x2+7.448 9x+0.026 7

c）在完成图5的各项计算基础上，可以进行图6的逐板计算。根据逐板计算的方法，首先若塔顶为全凝器，则xD=y1，代入拟合的气液平衡方程中，用Excel单变量求解功能，进行非线性方程求解液相平衡组成x1。这里初值的选择非常重要，否则会不收敛。

具体做法是选择目标单元格和可变单元格，输入拟合的6次多项式的函数式，在Excel工作表中菜单选择“数据”中的“模拟分析”如图所示，选择单变量求解，输入相关单元格和目标值，本例中目标单元格的目标值为xD=y1=0.859 7，确定后即可算出x1。代入精馏段操作线方程即可算出y2，再以下一组单元格作为目标单元格和可变单元格，输入拟合的6次多项式的函数式：

=-68.42 A631+207.74 A531-247.64 A431+147.38 A3311-45.822 A231+7.446 7 A31+0.026 7

式中：A31 —A31单元格的变量输入值。

目标值输入y2的值，确定后即可算出x2，以此交替使用相平衡线和精馏段操作线，至入口进料浓度后转向提馏段操作线和相平衡线进行计算。继续重复计算，直到xN≤xW為止。计算过程如图8（a、b、c）所示。

d）每个梯级包括一个水平线段和一个垂直线段。水平线段气相线值相同，垂直线段是液相线的值相等。根据这个特点在完成图6的逐板计算后，将每块塔板的气液相组成进行如图7所示的排列，为进行画梯级做准备。

e）在图4上继续点击右键，选择“选择数据”出现“选择数据源”对话框，按此操作选择“添加”按钮，完成精提馏段数据选定，即可在散点图上画出此两条直线。至此已绘制完成了相平衡线、对角线、求最小回流比的切线、精馏段和提馏段的操作线。在图7基础上进行梯级的绘制过程。同样重复在图上点击右键，选择“选择数据”出现“选择数据源”对话框，按此操作选择“添加”按钮，如图9所示，完成图7所示的27组坐标点-线段选择添加，即可完成整个图解过程。结果如图10所示。

通过逐板和图解相结合，利用Excel的计算和图表功能，最大的特点是不需要复杂的编程完成复杂和繁琐的逐板迭代计算完成了非理想体系的理论板计算和图解问题。该法具有一定的通用性。在本例中的具体计算结果如表3所示。

2  说明及结果讨论

（1）对于理想的二元物系，有固定的相对挥发度，即有固定形式的相平衡方程对于非理想的二元物系，相对挥发度不再是定值，即没有固定形式的相平衡方程，需要用若干个气液平衡数据拟合平衡关系式。其实，二元理想物系的情况可以看成是二元非理想物系里的一种特殊情况。

对于非理想物系的情况在拟合气液平衡数据关系时如果用多项式拟合，多项式的次数选择很重要。从图11可以看出，6次多项式拟合的效果最好。3次和4次误差较大，时景荣等[2]给出用Excel图解法求精馏塔理论塔板数的通用程序，用VBA编程的方法完成理论塔板数的计算。曾讨论认为用5阶多项式拟合将在x值低时震荡而失败，用4阶多项式拟合也产生很大的偏差，梯级线与气液平衡线产生一定的偏离，认为选择一元三点插值多项式拟合编程效果较好。而本法不采用编程方式完成多项式方程的求根问题，采用图5-6的计算数据可以缩小估计初值的区间，从而使求根区间在很小的范围内搜索，不会造成发散情况的发生。

回流比是精馏的核心，因此，确定最小回流比Rmin有重要的意义。这在很多文献中涉及到[6，21]。本例乙醇-水非理想体系平衡线的特点，采用切线方式解决Rmin的确定。用试差方法获得切点（挟点）位置。因切点同时满足切线方程和拟合多项式方程，试差的准切点（x1，y1）与（xD，xD）做直线方程，若y1值与x1代入拟合多项式（相平衡方程）计算值相等，即可确认挟点位置，所求直线则为切线。若不等，则另试取x2（根据x1的值确定搜索方向和步长）则根据多项式计算的值y2与直线方程计算的值比较后判定是否满足条件。很容易确定此切线。

在进行理论板图解过程中，非理想体系的相平衡线和对角线非常接近的情况下，绘制梯级非常困难，而通过Excel提供的放大功能，很容易对局部进行放大从而使绘制梯级变得简单，提高了图解的精度。

3  结论

利用Excel的计算功能，图表功能，将逐板计算法和图解法相结合，利用逐板计算法时充分利用Excel的计算拟合功能，避免繁琐的编程问题，省事省力，方便快捷，计算精度高。同时在逐板计算的基础上，获得详细的精馏塔板的气液两相的详细信息，在此基础上进行理论板图解，方便直观地将逐板计算的结果进行形象地表达，同时又提高了图解法的精度。该方法具有一般性，能用于解决理想和非理想物系的二元组分的精馏理论塔板数的计算。Excel软件的普遍应用，为课堂教学和工程计算提供了计算和制图工具。

参考文献：

[1]田文德，刘晶晶，等.化工原理精馏过程的计算机辅助计[J].计算机与应用化学，2005， 10（20）：101-104.

[2]时景荣，罗传义，等.用Excel图解法求精馏塔理论塔板数[J].计算机与应用化学. 2005， 7（6）：162-166.

[3]譚天恩，窦梅，等.化工原理[M]. 第3版.北京：化学工业出版社， 2006：190-197.

[4] 陈敏恒，等.化工原理下[M]. 第1版. 北京：化学工业出版社，1986：70-78.

[5]贾绍义，柴诚敬，等.化工原理[M].第4版.北京：化学工业出版社，2013：112-118.

[6]李浩杰，王延伟.用VB逐板法计算精馏塔理论塔板数[J].计算机与应用化学， 2013，30（02）：183-191.

[7]刘奇琳，等.基于Excel的精馏理论塔板数的求解设计[J].高师理科学刊，2010，11（5）：126-130.

[8]陈洪钫，刘家祺，等.化工分离过程[M].第2版，北京：化学工业出版社，1995：20-31.

[9]曾平，等.计算机绘图求非理想溶液精馏理论塔板数[J].内江师范学院学报，1998，10（04）： 21-30.

[10]姜凯华，孟献梁，等.C++在精馏塔的理论板计算中的应用[J].中国科技论文， 2008 ，3（9）： 677-680.

[11]陈昀，刘红茹，等.计算精馏塔理论塔板数新方法的开发[J].计算机与应用化学，2007，7（05）： 681-684.

[12]杜迎春， 等. 基于Mathematica的二元连续精馏塔理论板层数新计算方法[J]. 计算机与应用化学，2009，26（10）：1319-1323.

[13]石秋忠，周颖华.应用Maple软件计算精馏理论板数[J].计算机与应用化学， 2013，30（02）：183-191.

[14]丁曙光，等.AutoCAD在精馏塔设计中的应用[J].化工设计通讯， 2005，7（04）： 37-40.

[15]李本祥，王映红.Matlab在图解法求精馏塔理论塔板数教学中的应用[J].人力资源管理，2017，10（05）： 249-250.

[16]倪俪文，任世学.Origin 9.0在精馏理论板层数求解中的应用[J].广州化工，2018，46（06）： 35-42.

[17]吴晓艺，王静文，等.牛顿插值算法在精馏塔理论塔板数计算中的应用研究（英文）[J].计算机与应用化学，2009，26（06）： 770-772.

[18]杨莹，高维平.精馏塔最小回流比求解方法[J].计算机与应用化学，1995，7（02）： 152-154.

[19]郑旭煦，等.二元精馏最小回流比的一神通用算法[J].渝州大学学报（自然科学版） ，1996，30（03）：113-117.

[20]叶世超，等.三次样条函数拟合平衡曲线求最小回流[J].成都科技大学学报，1994，14（02）： 20-24.

[21]高怀，等.流程模拟软件在甲醇精馏塔中的应用[J].当代化工， 2017，10（05）： 120-124.