从观察到思考——论数学解题中的思维拓展

杨君伟

(山西省晋城市第一中学校 048000)

俗话说得好：“智慧源于思考，思考源于观察.”对同一个问题，从不同的角度去观察，往往可以给我们带来不一样的思考和不一样的方法，这正是一题多解的形成原因.另外，在高中数学问题的解答过程当中，如何有效地突破一些较为复杂的难点，最关键的地方还是要通过观察来进行.那么如何通过有效的观察来实现题目的多样化求解呢？这就是本篇文章所要讨论的问题.

一、观察字母变量

在解题过程中首当其冲的一个重要观察角度就是要对相应的字母变量进行观察.有时我们需要观察变量的个数，并进一步思考如何消元或换元(比如函数问题)；有时我们需要观察变量的属性，并进一步思考选用什么知识工具去处理问题(比如解三角形问题)；有时我们需要观察变量的次数，并进一步思考如何设计求解路径.以下举一例说明：

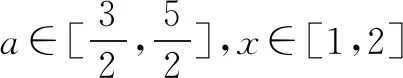
二、观察式子结构

通过观察式子结构往往可以帮助我们构造恰当的函数模型，比如：在导数应用小题中，我们需要根据导数不等式构造合适的原函数解题；在数列通项公式求解题型中，我们需要观察条件等式的特点，来选择通项公式求解方法；在解三角形问题中，我们需要观察已知等式的结构特点来判断是应该“角化边”还是应该“边化角”.以下举一例说明：

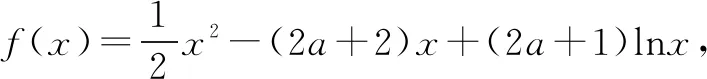
高中数学当中有很多重要的公式、性质，通过对题目所给式子的结构进行观察以及变形思考，能够更快地将这些题目与已经学到过的公式、性质等建立联系，快速构建解题思路.

三、观察运算特点

数学的推理离不开运算，而对运算特点的仔细观察，常常能帮我们寻找到正确的解题方向.这样的观察角度多见于不等式类问题，比如利用基本不等式求最值，利用对数平均值不等式解决极值点偏移问题，以及在自招或竞赛中常见的柯西不等式的应用等.以下举一例说明：

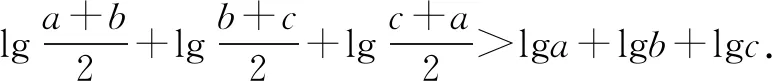
这个题目的左端变量位于真数位置，而且是“和式”运算，这不利于我们对左端式子进行变形分析，因为我们都知道，真数位置如果是乘除运算，是可以进行式子变形化简的，但是这里真数的“和式”运算，怎么样才能转化为“乘除”运算？再观察到左端和右端并不相等，所以我们可以利用不等式将“和式”化为“积式”，用到的工具当然就是基本不等式.

四、观察条件联系

对于题目已知条件的观察，主要是观察条件之间的联系，这在向量问题、立体几何问题等题型中较多见.当然，任何数学题目的求解都离不开条件的观察，这里所强调的，是在条件繁多的情况下，我们要着重观察分析条件之间的联系.以下举一例说明：

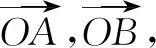
五、观察图象图表

数形结合是数学中非常重要的思想，其中的“形”指的就是图象图表.我们通过观察图象图表，可以直观感受到研究对象的变化规律，进而引导我们进行严谨论证，理解问题的“本质”.在解题过程中，观察图象图表可以帮助我们快速理解题意，有时也可以帮助我们找到巧妙解.以下举一例说明：

例5 已知函数f(x)=aex-x-1，若f(x)≥0对于任意的x∈R恒成立，求实数a的取值范围.

文中提到的五种有关高中数学解题过程中的观察角度都是因时而动的.对于不同类型的数学问题，有的时候可能需要结合多种类型的观察方式才能够得出美妙的结果，同学们要在平时的训练中细心体会，长期积累，方能做到灵活应用.