基于未知荷载系数法的斜拉桥索力优化
刘 军
(山西省交通科技研发有限公司 太原 030032)
斜拉桥作为高次超静定组合结构体系,具有结构跨度大、梁体自重轻,以及造型优美等特点,斜拉索能够有效地改善斜拉桥的内力分布情况和线形平顺程度,使其达到合理成桥状态[1]。如何进行索力优化一直是斜拉桥设计的核心问题,国内外学者针对该问题进行了一系列的研究,并取得较好的成果,将斜拉桥索力优化方法分为指定结构状态、无约束优化法、有约束优化法和影响矩阵法[2-4]。前3种优化方法由于只考虑了单一的目标函数,其各自使用范围具有一定的局限性。影响矩阵法综合了以上3种优化方法,将多种目标函数进行统一,解决了单一目标函数优化的缺点[5]。
未知荷载系数法的本质为影响矩阵法,采用未知荷载系数法计算斜拉桥最优索力具有高效性和精准性等特点[6]。本文结合具体的斜拉桥工程,采用未知荷载系数法计算斜拉桥的最优索力,具有一定的工程实践价值。
1 未知荷载系数法
1.1 未知荷载系数法原理
未知荷载系数法是通过设置斜拉桥的约束条件,求出满足约束条件的合理变量值,其计算理论基础为影响矩阵法。
结构满足线性叠加原理,因此
D=CX
(1)
式中:D为受调向量;C为影响矩阵;X为施调向量。
结构的弯曲应变能可写成
(2)
对于离散的杆系结构可写成
(3)
式中:m为结构单元总数;Li、Ei、Ii分别为i号单元的杆件长度、材料弹性模量和截面惯性矩;MLi、MRi分别为单元左、右端弯矩。
将式(3)改写成
U=MLTBML+MRTBMR
(4)
式中:ML、MR分别为左右端弯矩向量;B为系数矩阵;对角元素为
(5)
令调索前左右端弯矩向量分别为ML0、MR0,施调索力向量为T,则调索后弯矩向量为
(6)
式中:CL、CR分别为索力对左右端弯矩的影响矩阵。将式(6)代入式(4)得
(7)
式中:C0为与T无关的常数。
要使调整后结构应变能最小,令
(8)
式中:l为调整索数。
式(7)代入式(8)并写成矩阵形式
CLTBCL+CRTBCRT=-CRTBMR0-CLTBML0
(9)
取弯曲应变能与拉压应变能之和为目标函数,将方程式两端的影响矩阵用索力相应于相应截面内力的影响矩阵取代即可得到最优索力方程。
采用有约束的最小能量法对结构进行优化,可选结构的总势能作为优化目标函数。使用midas Civil软件建立有限元模型,根据有限元模型求出单元两端弯矩向量ML0、MR0和索力对弯矩的影响矩阵CL和CR,最后求解方程(9),进而求出拉索索力向量T。
1.2 未知荷载系数法步骤
1) 根据斜拉桥设计参数建立三维模型,其中:主梁、索塔和基础均采用梁单元模拟,拉索采用桁架单元模拟。
2) 根据实际情况将结构自重、二期恒载和拉索单位初拉力输入模型中,并进行荷载组合。
3) 采用分析模块进行结构分析。
4) 利用软件中未知荷载系数功能,设置斜拉桥成桥状态时需要满足的控制条件,通过影响矩阵法求出未知荷载系数。未知荷载系数法计算流程图见图1。

图1 未知荷载系数法计算流程图
2 建模分析
2.1 工程概况
斜拉桥为单塔双跨混凝土结构,跨径组成为98 m+98 m=196 m,索塔高度H为46.15 m,高跨比为0.471。桥宽27.5 m,设双向六车道,桥面布置为1.5 m+0.5 m+11 m+0.5 m+0.5 m+0.5 m+11 m+0.5 m+1.5 m=27.5 m。索塔为花瓶型索塔,总高度81.0 m,由于地形较深,在索塔下部有18 m的混凝土主墩。拉索布置形式为扇形双索面,全桥共设48根、12组斜拉索,斜拉索在主梁上的标准索距为8.0 m,其中,斜拉桥拉索由桥塔到桥台编号依次为A1~A12。斜拉桥总体布置图见图2,斜拉索编号示意见图3。

图2 斜拉桥总体布置图(单位:cm)

图3 斜拉桥拉索编号图
2.2 建立有限元模型
全桥共分为191个节点和190个单元(其中梁单元142个,桁架单元48个)。变截面部分采用变截面单元进行处理,该模型边界条件及连接方式均按照斜拉桥设计情况对支座和连接状态进行模拟,全桥有限元模型图见图4。
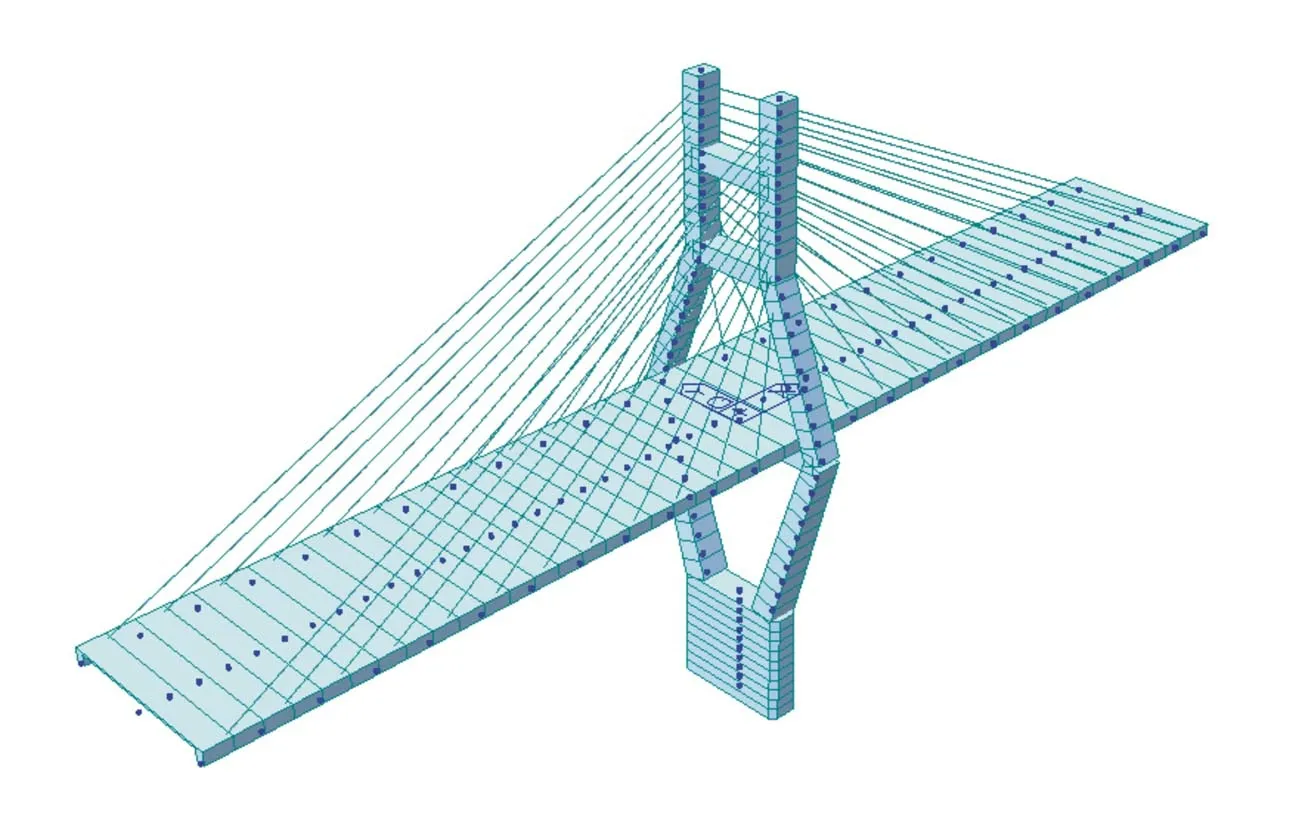
图4 全桥有限元模型图
斜拉桥主梁、拉索、索塔和钢筋材料参数表见表1。

表1 材料参数表
将斜拉桥自重、二期恒载和拉索单位初拉力依次添加到模型中。荷载模拟值如下。
1) 自重。自重包括一般梁单元的自重,拉索的桁架单元自重及横隔板的节点荷载自重,横隔板节点荷载取185 kN。
2) 二期恒载。二期恒载用连续荷载模拟,取122.5 kN/m。
3) 拉索初拉力荷载。拉索用桁架单元模拟,向每根拉索输入单位初始拉力1 kN。
斜拉桥边界条件见表2,表中x、y、z分别为纵桥向、横桥向和竖向,0表示自由,1表示在地面固结或2个构件之间相互约束。
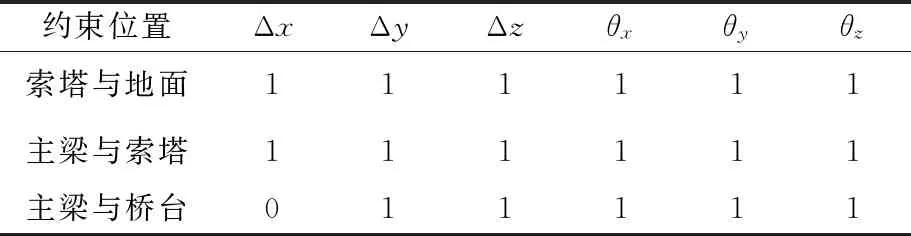
表2 斜拉桥边界条件表
2.3 优化目标
斜拉桥理想的控制目标应该使斜拉桥结构充分发挥其材料性能,达到经济最优化,在该状态下的索力为最优索力。根据斜拉桥自身特点,在恒载作用下,应尽量使塔顶水平位移和主梁竖向位移最小。因此,以斜拉桥桥塔水平位移和主梁竖向位移最小为目标对索力进行优化,寻求最优的成桥索力。该目标函数可以表达为
min{max[f(x)]}
(10)
式中:max[f(x)]为结构的最大变位值;x为斜拉索初张拉力。
2.4 约束条件
斜拉索在成桥状态下,每根拉索均受力;考虑到斜拉索强度和疲劳问题,需要限定索力的最大和最小值。因此,斜拉索索力的约束条件可表示为
(11)
式中:x为斜拉索初张拉力列阵;PD为索力在结构自重作用下的列阵;PA为索力在单位索力作用下的影响矩阵;Pmax、Pmin为指定拉索索力最大和最小值。
斜拉桥在成桥状态下,主梁竖向位移和主塔水平位移是重要指标。因此,斜拉桥设计需要限制主梁和塔顶的位移值,约束条件如下。
(12)
式中:DD为结构在自重作用下的节点位移列阵;DA为节点位移的影响矩阵;Dmax、Dmin为指定节点位移的最大和最小值。
2.5 成桥索力优化结果
根据斜拉桥合理成桥状态的要求,将索塔塔顶位移、主梁内力和主梁竖向挠度设为约束条件。约束条件如下:主梁弯矩绝对值≤10 000 kN·m;索塔塔顶位移≤10 mm;主梁竖向挠度≤20 mm。通过控制斜拉桥成桥状态时需要满足的条件,利用影响矩阵进行索力优化,得出成桥阶段最优索力,索力优化结果及设计索力值见表3,优化后的索力见图5。

表3 计算索力与设计索力对比表

图5 优化索力折线图
由图5可知,斜拉桥每根拉索拉力均为正值,表明每根拉索都处于工作状态。此外,两端拉索索力最大,并且拉索索力大小随着拉索编号的增大而增大,该索力分布形式可以有效提高桥梁承载能力,同时限制索塔塔顶位移,满足合理成桥状态下的索力分布规律。根据计算索力与设计索力对比表可得,拉索优化后的索力值与设计索力值非常相近,最大相对误差仅为3.33%,故采用未知荷载系数法对斜拉索进行优化是合理的。
2.6 成桥状态下斜拉桥结构验算
成桥状态下斜拉桥结构验算包括:主梁强度和挠度变形验算、索塔强度验算和拉索强度与疲劳验算。由于篇幅所限,在此只展示主梁挠度变形验算和拉索强度与疲劳验算。
将优化后的索力值输入模型中,并添加相应的汽车荷载、温度荷载,在软件中进行作用组合并验算。现取基本组合(1.2×恒荷载+1.0×收缩及徐变引起的二次效应+1.4×汽车荷载+1.05×体系降温和正温度梯度)对斜拉桥进行结构验算,主梁挠度变形验算结果见表4,拉索强度和疲劳验算结果见表5。

表4 主梁挠度变形验算表

表5 斜拉索强度和疲劳验算表
由表4可知,基本组合下主梁挠度变形最大值为0.112 m,小于斜拉桥规范规定L/500=0.196 m,故主梁挠度变形满足要求。由表5可知,基本组合下斜拉索最大应力为285 MPa,小于斜拉索控制应力930 MPa和斜拉索应力幅300 MPa,故斜拉索强度和疲劳满足要求。
3 结语
依托具体斜拉桥项目,以成桥状态优化的主梁和塔顶位移为优化目标,主梁弯矩为约束条件,采用未知荷载系数法计算斜拉桥最优索力,优化后的索力值随着拉索编号增大而增大,满足合理成桥状态下的索力分布规律,且其与设计值非常相近。同时对成桥状态下的斜拉桥进行结构变形、强度及疲劳验算,验算结果表明满足规范要求。通过计算证明,未知荷载系数法可以作为斜拉桥索力优化计算的一种有效方式,可以为斜拉桥的设计计算提供一定的依据。

