针对平行航路的改航路径规划研究

王莉莉，刘子昂

(中国民航大学 空中交通管理学院，天津 300300)

0 引 言

改航是一种能够有效解决空域拥堵问题的战术流量管理手段。国内外在改航路径规划研究方面均取得了一些有代表性的成果。在国外，J.KROZEL等[1]提出了自由飞行环境下的改航路径规划方法；J.J.PANNEQUIN等[2]研究了多架航空器在恶劣天气下的考虑冲突解脱的改航路径规划方法；A.V.SADOVSKY等[3]考虑了天气的不确定性条件，以期望改航路径最短为目标，给出了一定风险控制下的改航路径规划方法。在国内，笔者等[4-5]设计了流程简单、易于实现的启发式改航路径规划算法；徐肖豪等[6]、王兴隆等[7]、张兆宁等[8]引入动态避障能力较强的人工势场法规划改航路径；李雄等[9]、孟令航等[10]、王飞等[11]利用了其他能够灵活搜索路径的智能算法规划改航路径。

以上研究普遍没有结合相应的航路、空域结构进行因地制宜的分析，所考虑的改航环境过于理想化，没有从航路系统的角度进行改航路径规划。随着PBN运行的推广和星基导航的发展，安全风险低、运行效率高的平行航路作为重要的航路结构被越来越多地应用于空域规划中[12]。笔者以平行航路为研究对象，在充分考虑恶劣天气下平行航路实施改航可能面临的问题后，针对平行航路设计了相应的的改航路径规划方法，并以雷暴多发地西南地区新开通的“天路”——成拉复线[13]作为仿真对象验证了该改航策略的可靠性。

1 栅格环境下基于动态规划的改航路径规划

1.1 改航环境模型

当计划航路上出现恶劣天气时，飞机主要采用侧向绕飞的方式规避危险天气，故可以将飞机的改航路径规划空间视作二维平面。进一步，笔者将平面二维区域划分成若干个大小相同的方格使改航环境栅格化。改航问题中方格的边长通常设置为10、15、20 km，方格的横向划分线与计划航路平行。

设飞机的保护区半径为D，在天气信息更新的一个周期内，将探测到的恶劣天气区域按距离D向外做膨化处理得到恶劣天气限制区，如图1，几何图形的深灰色扩张区域即为膨化区域。由此，飞机在路径规划过程中可以被视为质点。将恶劣天气限制区完全侵占或部分侵占的方格称为决策失效方格，恶劣天气限制区完全没侵占的方格称为决策有效方格。决策有效方格在图形中用白色表示，决策失效方格在图形中用灰色表示，如图1。

1.2 基于动态规划的改航路径规划

通过动态规划分阶段求出由若干栅格的几何中心构成的决策序列，飞机的改航路径由这些栅格中心连接而成。然后根据飞行性能对得到的决策序列进行筛选，最终得到既能安全避障又能满足飞行性能的改航路径。设改航起始点Qs和改航结束点Qf已知，动态规划的流程如下:

1)阶段划分

按方格在横向划分空间阶段。以改航起始点Qs为起点，改航结束点Qf为终点，在横向上按顺序对Qs、Qf及其中间的若干栅格中心所在方格依次编号，如图2。

2)状态变量和状态集合

对任一阶段k(k=1,2,…f)对应的一列纵向方格按从下至上的顺序依次编号1,2,…,sk,max，此列方格的纵向编号构成的集合为阶段k的状态集合{sk}，方格的一个纵向编号对应阶段k的一个状态变量sk，如图2。因此，代表方格横纵编号的数组(x,y)与其所处阶段及状态一一对应，例如，方格(2,5)表示阶段2的状态5。另外，为了保证航空器能够在同一阶段内移动，新增一状态变量s′k，表示航空器在同一阶段状态移动后的纵向位置。

3)决策变量和决策集合

决策变量xk,(xk∈Z，Z表示整数)表示从阶段k的某一方格(k,sk)转移到阶段k+1的方格(k+1,sk+xk)上，即相邻两阶段状态对应的方格纵向编号差，如图2。对于航空器在同一阶段内的移动，为每一阶段新增一决策变量x′k，表示状态变量在同一阶段内转移的纵坐标差。

设E(x,y)表示方格(x,y)的决策有效性检测函数，E(x,y)的函数式满足式(1)：

(1)

当xk≥0时，决策变量xk要满足约束：

(2)

式中：xk∈Z，Z表示整数。

当xk<0时，决策变量xk要满足约束：

(3)

式中：xk∈Z-，Z-表示负整数。

当x′k≥0时，新增决策变量x′k要满足约束：

(4)

当x′k<0时，新增决策变量x′k要满足约束：

(5)

式中:关于xk+sk及x′k+sk约的束条件表示飞机的位置不得超过改航空间的边界；关于E(k,sk)和E(k+1,sk+1)的限制条件表示飞机在移动过程中不得进入恶劣天气限制区；约束条件x′k+sk≠sk-1+xk-1表示飞机在当前阶段的纵向移动要受前一阶段斜向移动的约束。

4)状态转移方程

根据决策变量xk所代表的意义，前后两阶段衔接的状态方程可以设置为：

sk+1=sk+xk+x′k

(6)

5)阶段指标函数

改航路径规划的主要目标之一是路径长度最短，故指标函数设置为从阶段k的到阶段k+1所走过的路径长度，表示为：

(7)

6)递推方程

设fk(sk)代表从阶段k的sk状态出发到达终点的最优指标函数，利用逆序法求解该动态规划最优值的递推方程可以表示为：

(8)

式中：N表示总阶段数。

7)决策序列筛选

考虑到飞机的飞行性能和乘客的舒适度，改航路径需满足2个条件：①相邻转弯点间的距离d≥7.4 km；②转弯角度θ≤90°[14]。由于相邻栅格中心的间距l≥7.4 km，故条件①已经满足，但为了继续满足条件②，仍需对步骤1～步骤5中计算出的若干决策序列进行筛选，筛选流程如下：

步骤1：将各决策序列按照目标函数值的大小从小到大排序，设Pi代表第i个决策序列，令i=1；

步骤2：设θi(m),m=1,2,…表示第i个序列中每一阶段的状态变量对应的转弯角度，利用余弦定理计算θi(m),m=1,2,…是否小于90°；

步骤3：若满足θi(m)≤90°,m=1,2,…，则转至步骤5；

步骤4：若存在θi(m)>90°，则令i=i+1，转至步骤2；

步骤5：输出该决策序列，该决策序列对应栅格几何中心连接成的路径即为改航路径。

笔者将栅格环境与动态规划相结合得到了一种新的改航路径规划方法，并根据飞机飞行性能对决策序列进行筛选，最终规划出一条既满足路径取短要求，又满足飞机飞行性能的改航路径。该方法简单易行，不会陷入局部最优解，既可以用于规划单雷暴下的改航路径，也可以用于规划多雷暴下的改航路径。

2 平行航路的改航优先权机制

2.1 平行航路改航涉及的问题

笔者仅研究中小尺度恶劣天气下的改航，对大尺度恶劣天气下飞机无法做局部路径调整的问题不做研究。平行航路的改航问题是个系统问题，在恶劣天气天气的影响下，原本相对独立运行的两条航路变成了两个相互影响的子系统，这其中既涉及到安全保障问题也涉及到经济优化问题，具体问题如下：

1)冲突碰撞问题

如果存在飞机在平行航路的内侧区域实施改航，那么可能导致原本平行运行的飞机间产生飞行冲突甚至碰撞，如图3(a)。

2)区域入侵问题

如果存在飞机沿平行航路的外侧实施改航，那么会有因外侧部分的限制区面积较大而使改航范围过大进而冲入临近扇区的可能，在边境地区甚至有改航至邻国空域的风险，如图3(b)。

3)经济优化问题

如果两条平行航路的内侧、外侧改航空间均有一定的裕度，那么在保证飞行安全的前提下如何分配平行航路周围的空域资源才能优化两条航路的整体经济效益，即如何降低两条平行航路上飞机在改航段的燃油消耗量之和。

2.2 改航优先权机制

针对2.1节中提出的中、小尺度恶劣天气影响下平行航路涉及的几个问题，笔者采用改航优先权机制来解决这些问题[15]。改航优先权机制的基本思路是首先依据一定的规则对两条平行航路上运行的飞机做优先权分配，然后在不考虑低优先级飞机的情况下，先为高优先级飞机i规划改航路径Pi(S1)={x1(S1),…,xn(Sn)}，最后将高优先级飞机的改航路径区域视作飞行限制区(E(Si,xi(Si))=0,i=1,…,n)，再为低优先级飞机j规划改航路径Pj(S1)={x1(S1),…,xn(Sn)}。

改航优先权分配机制包括安全性原则和经济性原则。为了保证安全第一，要首先使用安全性原则进行优先级分配。如果两条航路上的飞机均满足相应的改航安全性，再使用改航经济性原则进行优先级分配来提高整体经济效益。

2.2.1 安全性原则

安全性原则如下：

1)当一条航路上运行的飞机发生特情(例如飞机单发失效，机内乘客需要急救等)处于紧急状态时，该平行航路上的飞机获得改航优先权。

2)当一条航路靠近管制区边界且恶劣天气区域占据范围较大，导致沿平行航路外侧不易实施改航时，该航路上的飞机获得改航优先权。判别方法为首先规划出在改航优先权赋予航路i(i=1,2)的情况下，航路j(j=1,2)对应的改航路径lij(i=1,2;j=1,2)。然后检查是否存在改航路径lij(i=1,2;j=1,2)超过管制区边界，若存在，则将取消航路i(i=1,2)的改航优先权，将改航优先权赋予另一条航路。

2.2.2 经济性原则

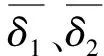
在该时段内，分别给航路1、2分配改航优先权对应的两条航路的改航燃油消耗量之和W1、W2为：

(9)

将W1、W2作差来比较W1、W2的大小关系：

(10)

气象信息每隔一段时间做一次周期更新，在恶劣天气侵占平行航路的某一周期内，改航优先权分配的流程如图4。

3 算例仿真

以成拉复线为对象验证平行航路改航策略的有效性。如图5，成拉复线地处我国西南边陲地区，该地区为雷暴多发区域，且紧邻国境线，改航是该地区的经常用到的空中交通流量管理措施。某一时段，昌都—拉萨段平行航路存在处于消散阶段的中尺度雷暴天气，且该雷暴天气已分解成若干个不断缩小的雷暴区域块同时影响两条平行航路(图5中A区域)。设拉萨—昌都方向的航路为航路1，昌都—拉萨方向的航路为航路2，在天气信息更新的某一周期内，预计有一架B737-800和一架A320-232通过航路1，两架B737-800和一架A320-232通过航路2，且这5架飞机均无特情状况出现，现通过笔者提出的平行航路改航路径规划方法为这五架飞机规划改航路径。

取飞机保护区半径D=1 km，对雷暴区域做膨化处理后将其栅格化得到改航环境。如图6(a)，经计算，在改航优先权分配给航路1的情况下，航路1的最优改航路径为①，航路2的最优改航路径为④；在改航优先权分配给航路2的情况下，航路1的最优决策序列为②，航路2的最优决策序列为③。由于飞机飞行性能正常且改航空间裕度足够，故两条航路上的飞机均满足改航安全性，由图4的改航优先权分配流程，接下来由经济性原则分配改航优先权。

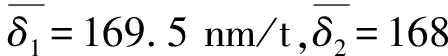
如图6(b)，如果利用几何算法的规划改航路径，航路1、2上的飞机将分别沿路径⑤、⑥改航，此时的改航总里程为616 km，消耗的总燃油量为5 t。笔者提出的改航路径规划方法与之相比总里程缩短了5%，总燃油消耗量节约了8%。由此可见，笔者提出的针对平行航路的改航路径规划方法不仅保证了飞行安全性，同时也能有效提升改航经济性。

4 结 语

首先给出了一种既能对单雷暴也能对多雷暴规划改航路径的方法，该方法简单易行，不会陷入局部最优解等智能算法遇到的问题。然后设计了改航优先权机制来解决平行航路改航可能遇到的安全保障问题和经济优化问题。最后将西南地区的成拉复线作为对象进行算例仿真。仿真结果表明，笔者提出的针对平行航路的改航路径规划方法既保证了飞行安全又节约了燃油消耗，实现了节能减排的目标，对实际运行具有较强的指导意义。