基于分形理论的高煤阶煤岩渗透率计算方法研究与应用

王镜惠　梅明华　刘娟　王华军

摘      要：为了提供有效的煤岩渗透率计算方法，基于分形理论推导了煤样渗透率计算模型，提出了相应参数的获取方法，基于高压压汞实验获得的毛管压力数据和实验测得的相应煤样的渗透率数据验证了计算方法的正确性，并基于该方法利用数值模拟的方法分析了煤样渗透率的主要影响因素。结果表明，分形理论的煤岩渗透率计算方法能够有效预测煤岩渗透率，平均误差仅为6.84%;煤岩分形维数、迂曲度和最大孔隙半径对渗透率具有重要影响，煤岩渗透率随着分形维数和迂曲度增加而降低，随最大孔隙半径增加而增加。

关  键  词：分形理论;高煤阶;煤岩;渗透率;计算方法

中图分类号：TQ021.4       文献标识码： A      文章编号：1671-0460（2020）07-1356-05

Research and Application of the Permeability Calculation

Method for High-rank Coal Rock Based on Fractal Theory

WANG Jing-hui1a， MEI Ming-hua2， LIU Juan1b， WANG Hua-jun2

（1. a.School of Chemistry and Chemical Engineering;1b. School of life Science，Yulin University， Yulin Shaanxi 719000， China;

2. The Second Gas Production Plant of PetroChina Changqing Oilfield Branch Company， Shaanxi Yulin719000， China;

Abstract： In order to provide effective calculation method of the coal rock permeability， the permeability calculation model of coal samples was deduced based on the fractal theory， and the acquisition approach of corresponding parameters was proposed. The correctness of the calculation method was verified based on the capillary pressure data from high-pressure mercury injection experiments， and the main influencing factors of the coal sample permeability were analyzed based on the permeability calculation model. The results showed that the permeability calculation method of high-rank coal rock based on the fractal theory could effectively predict the permeability， and the average error was only 6.84%. The fractal dimension， tortuosity and maximum pore radius of coal rock had important influence on its permeability. And the permeability of high-rank coal rock decreased with the increase of fractal dimension and tortuosity， and increased with the increase of maximum pore radius.

Key words： Fractal theory; High coal rank; Coal rock; Permeability; Calculation method

煤層气储层渗透率对开展煤层气储层评价，实现煤层气井高产稳产具有重要意义^[1]。煤层气储层一般需要通过压裂提供渗透率^[2]，但煤层原始渗透率对煤层气开发起决定性作用。煤层气储层为低孔低渗储层，孔隙结构复杂，煤样制取难度较大且渗透率测试较难，迫切需要有效的渗透率计算模型。许多学者对致密砂岩储层渗透率预测进行了研究，如邓浩阳等研究了基于致密砂岩储层孔隙结构参数，利用多元回归的方法建立渗透率计算模型^[3];张涛等建立了致密砂岩储层绝地渗透率计算模

型^[4];范宜仁等基于三组分法建立了致密砂岩岩心核磁共振渗透率表征新模型^[5];而对于煤岩渗透率的研究则多为实验测试，缺乏成熟的计算方法，刘帅帅等以鄂尔多斯盆地东缘柳林矿区南部4号煤层为研究对象，研究了有效应力对煤储层不同方向渗透率的影响^[6]。牛丽飞等以山西潞安常村矿3号煤层圆柱试样为对象，测试并研究了垂直层理和平行层理方向煤体渗透率变化特征^[7]。魏建平等基于裂隙平板模型，理论推导了瓦斯解吸、扩散及渗流过程中煤体渗透率的变化关系，认为渗透率与瓦斯压力的关系呈现一种非对称“U”字型变化规律^[8]。刘永茜等通过建立描述煤体孔隙和裂隙渗透率统一数学模型，将煤体内气体渗流分为孔隙控制型、裂隙控制型和孔隙-裂隙联合控制型3类^[9]。付新等对煤岩孔隙结构进行了研究，并将进汞量约25%处的煤岩孔隙半径与渗透率进行回归，得到渗透率预测方

法^[10]，但该方法仅基于数学统计，缺乏理论基础。李立功等研究了考虑克林伯格系数的煤储层渗透率预测模型，但该模型参数众多，不适于现场应用^[11]。因此，文章引进分形理论对孔隙结构进行定量评价，并在此基础上推导了煤样渗透率计算方法，并基于高压压汞实验获得的毛管压力曲线验证了本文提供计算方法的正确性。

1  渗透率计算方法理论推导

许多学者研究表明，煤岩孔隙结构具有分形特征^[12-13]，则根据分形理论，煤岩孔隙数目与孔隙半径成幂率关系，则其定量表达公式为：

（1）

式中： N（>r）—多孔介质孔隙数量;

r —多孔介质孔隙半径;

a —常数;

D_f —分形维数。

由于煤岩孔隙结构复杂，孔隙数目巨大，N（>r）可近似看成连续可微函数，对其微分得到半径在r～r+dr范围内毛管孔隙数量为：

（2）

根据Poiseuille定律得到经过单根毛管孔隙圆形截面的流量为^[14]：

（3）

式中： q —单根毛管孔隙中流体流量;

dp —单根毛管孔隙进出口压力差;

τ —毛细管孔隙迂曲度;

μ —流体黏度;

l —毛细管孔隙长度。

基于毛管束理论，将煤样孔隙体系看作一个整体，并将其假想为一束具有不同孔隙半径的毛管束，但每根毛管具有相同直径，以此为理论基础，将q在r_min～r_max范围内积分，可得到煤储层渗流截面A上的总流量为：

（4）

式中： Q —渗流截面A上的总流量;

A —截面面积;

r_min —最小孔隙半径;

r_max —最大孔隙半径。

将式（3）和式（2）带入式（4）整理得：

（5）

根据达西定律，毛管内流量可以通过下式进行计算：

（6）

式中： K —煤层渗透率。

将式（5）和式（6）联立可得：

（7）

式（7）即为煤层气储层渗透率计算公式。由式（7）可知，煤层气储层渗透率主要取决于煤样分形维数和孔隙半径。

2  关键参数确定方法

根据式（7），计算煤岩渗透率需要获取分形常数a，分形维数D_f，最小孔隙半径r_min，最大孔隙半径r_max，毛细管孔隙迂曲度τ等5个参数。其中煤岩孔隙迂曲度τ一般在1.5～3.0之间，其余4个参数均通过煤岩毛管压力曲线获得，本文中毛管压力曲线通过高压压汞实验获得。

将式（1）两边取对数得：

（8）

则在双对数坐标中，N（>r）和r成线性关系，且斜率为-D_f。设直线斜率为k，截距为b，则

（9）

（10）

其中孔隙半径（r）可以利用煤岩压汞曲线通过式（11）求得：

（11）

式中： P_c —毛管压力;

σ —界面張力;

θ —汞与空气接触角。

根据式（11）求出的煤样孔隙半径分布范围，进而确定各煤样的r_min和r_max。不同孔隙半径的孔隙数量N（r）可以根据压汞实验数据计算得到：

（12）

式中：ΔV_Hg —与孔隙半径r相对应的同一进汞压力下的进汞体积。

3  实验验证

3.1  煤岩毛管压力实验

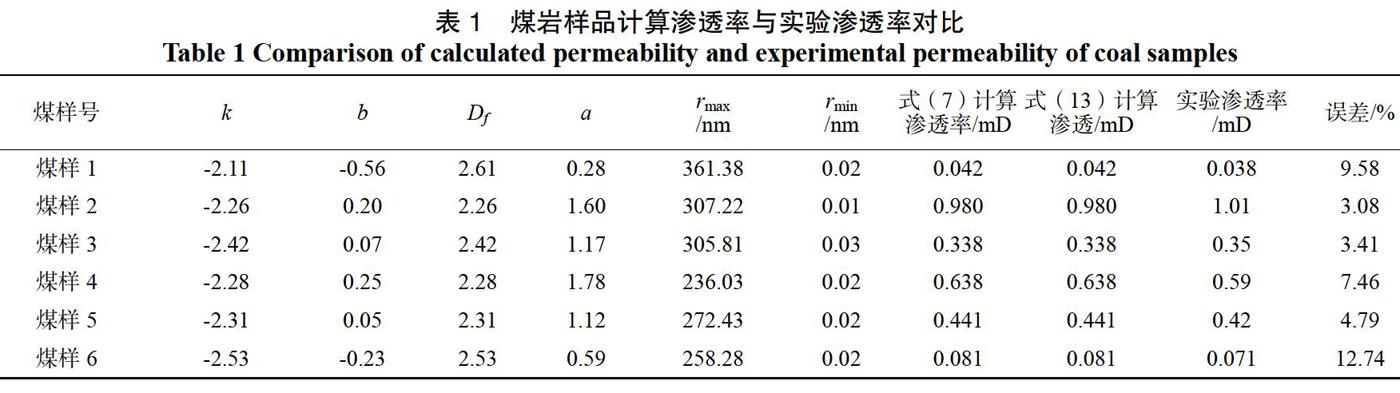
煤岩毛管压力实验样品取自沁水盆地南部煤矿，将大块煤样加工制作6块长度为50 mm，直径为25 mm的柱状煤岩样品，采用空气渗透率测试仪分别测定各个煤样渗透率，结果见表1，渗透率测试完毕后，利用各煤样在室温条件下开展高压压汞实验，得到6块煤样的毛管压力曲线如图1所示。

由图1可知，煤样1、5、6压汞曲线最为陡峭，曲线接近纵坐标轴，表明煤样物性较差，孔隙结构非均质性强。利用分形维数可以表征煤样孔隙结构的非均质性，分形维数越大，非均质性越强，煤样渗透率越低，煤样1、5、6中每样5的分形维数仅为2.31，表明其孔隙结构均质性较强，因此尽管其毛管压力曲线较为陡峭，但其渗透率仍然较高。煤样2、3、4压汞曲线形态相对较为平缓，存在中间相对平缓段，表明这3块煤样渗透性高于上述煤样，如表1所示，该3块煤样渗透率均大于0.35 mD，渗透率相对较高。但整体上除煤样4以外，5块每样中间平缓段均不太明显，这表明6块煤样孔隙结构整体复杂，为低渗透煤样。

3.2  渗透率计算及验证

根据式（11）、（12），利用上述6块煤样压汞曲线对应的数据，计算煤岩的孔隙半径（r）和对应的孔隙数量N（r），将两个参数取对数后绘制lg（r）与lg（N（r））散点图，结果如图2所示。图2表明，各煤样孔隙半径（r）和对应的孔隙数量N（r）在双对数坐标中均成线性关系，这进一步证明了各煤样孔隙结构满足分形特征。

分别对各煤样进行线性拟合，根据式（8）得到各煤样的k和b值，然后根据式（9）、（10）计算相应的D_f和a，然后从计算得到的孔隙半径（r）中读取r_min和r_max值，煤样迂曲度按1.75计算，最后根据式（7）计算各煤样渗透率，结果如表1所示。

4  煤岩渗透率影响因素分析

根据式（7），模拟分形维数、迂曲度、最大孔隙半径和最小孔隙半径对煤岩渗透率的影响，基本参数采用煤样2数值计算，结果如图3—图6所示。

4.1  分形维数影响

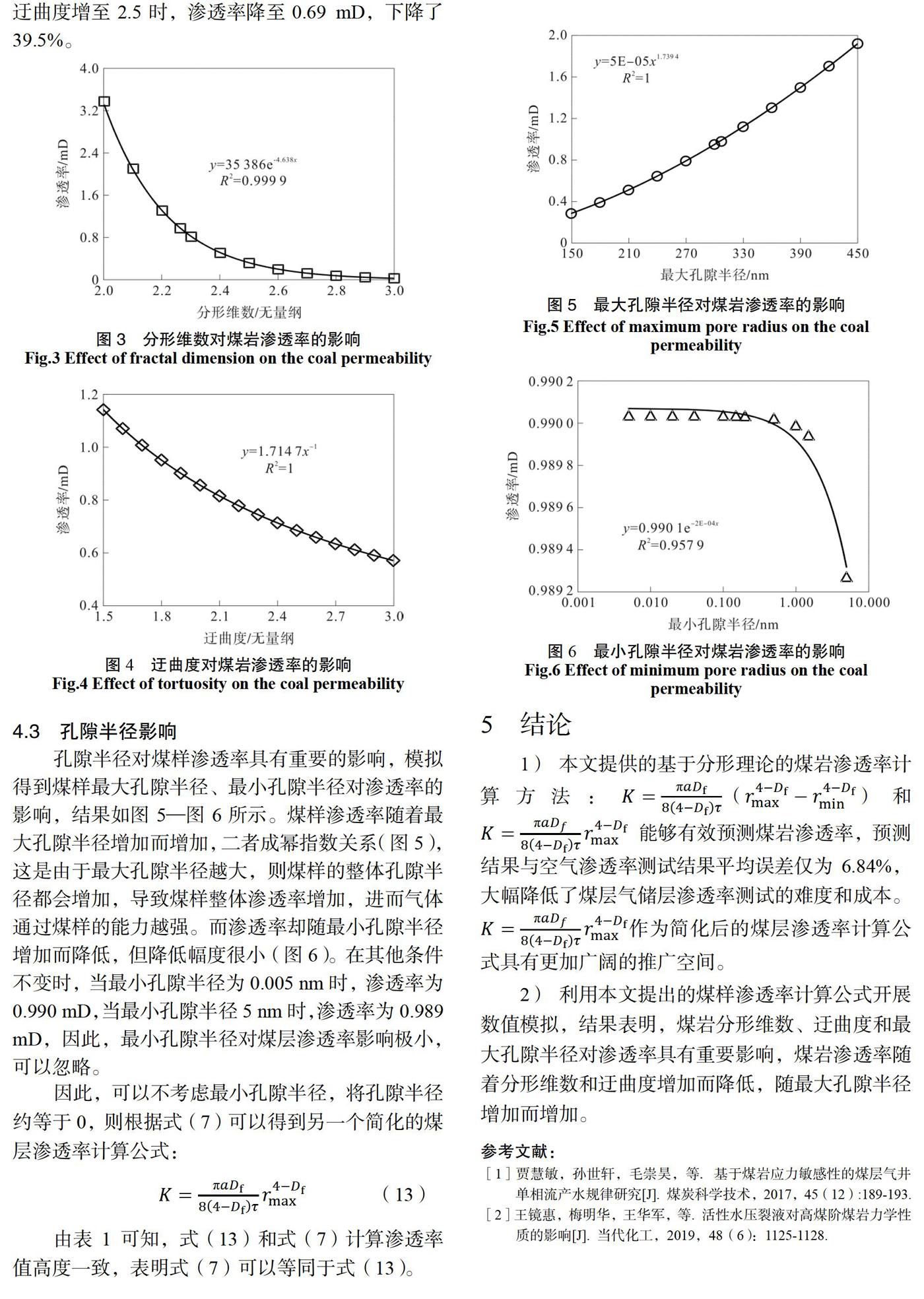
分形维数表征煤岩孔隙结构非均质性，分形维数越大，煤岩孔隙结构越复杂，非均质性越强，物性越差^[15]。由图3可知，煤样渗透率随着分形维数增加而降低，二者成负指数关系，且分形维数在2～2.5之间时，渗透率下降速度快，分形维数大于2.5后，渗透率下降速度变慢。如分形维数为2时，渗透率为3.38 mD，当分形维数增至2.5时，渗透率下降至0.32 mD，下降了91%;而分形维数为3时，渗透率比分形维数为2.5时下降了0.29，下降了90%。

4.2  迂曲度影响

煤岩迂曲度表征煤岩孔隙的弯曲程度，煤岩孔隙结构越复杂，弯曲度越大，迂曲度越大^[16]。由图4可知，煤样渗透率随着迂曲度增加而降低，二者反函数关系，且随迂曲度增加，渗透率降低速度先快后慢。如迂曲度为1.5时，渗透率为1.14 mD，当迂曲度增至2.5时，渗透率降至0.69 mD，下降了39.5%。

4.3  孔隙半径影响

孔隙半径对煤样渗透率具有重要的影响，模拟得到煤样最大孔隙半径、最小孔隙半径对渗透率的影响，结果如图5—图6所示。煤样渗透率随着最大孔隙半径增加而增加，二者成幂指数关系（图5），这是由于最大孔隙半径越大，则煤样的整体孔隙半径都会增加，导致煤样整体渗透率增加，进而气体通过煤样的能力越强。而渗透率却随最小孔隙半径增加而降低，但降低幅度很小（图6）。在其他条件不变时，当最小孔隙半径为0.005 nm时，渗透率为0.990 mD，当最小孔隙半径5 nm时，渗透率为0.989 mD，因此，最小孔隙半径对煤层渗透率影响极小，可以忽略。

因此，可以不考虑最小孔隙半径，将孔隙半径约等于0，则根据式（7）可以得到另一个简化的煤层渗透率计算公式：

（13）

由表1可知，式（13）和式（7）计算渗透率值高度一致，表明式（7）可以等同于式（13）。

5  结论

1） 本文提供的基于分形理论的煤岩渗透率计算方法： 和  能夠有效预测煤岩渗透率，预测结果与空气渗透率测试结果平均误差仅为6.84%，大幅降低了煤层气储层渗透率测试的难度和成本。 作为简化后的煤层渗透率计算公式具有更加广阔的推广空间。

2） 利用本文提出的煤样渗透率计算公式开展数值模拟，结果表明，煤岩分形维数、迂曲度和最大孔隙半径对渗透率具有重要影响，煤岩渗透率随着分形维数和迂曲度增加而降低，随最大孔隙半径增加而增加。

参考文献：

[1]贾慧敏，孙世轩，毛崇昊，等.基于煤岩应力敏感性的煤层气井单相流产水规律研究[J]. 煤炭科学技术，2017，45（12）：189-193.

[2]王镜惠，梅明华，王华军，等. 活性水压裂液对高煤阶煤岩力学性质的影响[J]. 当代化工，2019，48（6）：1125-1128.

[3] 邓浩阳， 司马立强， 吴玟， 等. 致密砂岩储层孔隙结构分形研究与渗透率计算——以川西坳陷蓬莱镇组、沙溪庙组储层为例[J].岩性油气藏， 2018， 30（6）： 76-82.

[4]张涛， 李相方， 王香增， 等. 致密砂岩气水相对渗透率模型[J]. 中国科学： 技术科学， 2018， 48（10）： 1132-1140.

[5]范宜仁， 刘建宇， 葛新民， 等. 基于核磁共振双截止值的致密砂岩渗透率评价新方法[J].地球物理学报， 2018， 61（4）： 1628-1638.

[6]刘帅帅，杨兆彪，张争光，等. 有效应力对煤储层不同方向渗透率影响的差异性[J]. 天然气地球科学，2019，30（10）：1422-1429.

[7]牛丽飞，曹运兴，石玢，等. 潞安矿区煤层渗透率的各向异性特征实验研究[J].中国安全生产科学技术，2019，15（9）：82-87.

[8]魏建平，秦恒洁，王登科，等. 含瓦斯煤渗透率动态演化模型[J]. 煤炭学报，2015，40（7）： 1555-1561.

[9]刘永茜，侯金玲，张浪，等. 孔隙结构控制下的煤体渗透实验研究[J]. 煤炭学报，2016，41（S2）： 434-440.

[10]付新， 薄舒月， 段宏臻， 等. 高煤級煤储层压汞特征分析及渗透率估算[J].长江大学学报（自科科学版）， 2018，15（15）： 64-67.

[11]李立功，康天合，李彦斌.考虑动态克林伯格系数的煤储层渗透率预测模型[J].地球物理学报，2018，61（1）：304-310.

[12]徐欣， 徐书奇， 邢悦明， 等. 煤岩孔隙结构分形特征表征方法研究[J].煤矿安全， 2018， 49（3）：148-150.

[13]杨宇，孙晗森，彭小东，等.煤层气储层孔隙结构分形特征定量研究[J].特种油气藏，2013，20（1）：31-33.

[14]路阳.关于泊肃叶定律的适用范围和定律的修正的讨论[J].物理通报，2016（4）：29-32.

[15]贾慧敏. 高煤阶煤岩孔隙结构分形特征研究[J]. 石油化工高等学校学报， 2016， 29（1）： 53-56.

[16]徐鹏， 邱淑霞， 姜舟婷， 等. 各向同性多孔介质中Kozeny-Carman常数的分形分析[J]. 重庆大学学报， 2011， 34（4）：78-82.

基金项目：榆林市科技计划项目（项目编号：2018-2-53）。

收稿日期：2019-11-06

作者简介：王镜惠（1984-），男，陕西榆林市人，讲师，硕士，2012年毕业于西安石油大学油气田开发专业，研究方向：油气地质勘探及油气田开发。E-mail： wangjinghui2219@sohu.com。