从某些一元二次方程的另类方法引起的思考

滕晓梅

摘要：从一道中考新题引到应用题的教学环节，通过多种方法的碰撞，体会数学伪生活化的危害。从具体的事例反思数学应用题的教学应该放手让学生去探讨-总结-回顾，进而建模。让学生充分体会学习的乐趣。

关键词：应用题;建模;伪生活化

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2020）14-106-2

浙江省2011年初中数学学业考试（衢州卷）的21题改编浙教版八年级下册36页的例1，这是一道印象深刻的例题，当时在教学这一内容时很还颇让我苦恼。至今教学片断还留在我的脑海中。现在把这一例题的教学片断呈现出来：

一、情境再现，发现问题

1.创设情境

师：方程是刻画数量关系的典型模型，现在让我们共同回顾列方程解应用题的基本步骤有哪些？

生1：找数量关系根据数量关系列方程

生2：审题→设元→列方程→解方程→答

师：主要流程不错，其实大体上分四个步骤：⑴理解问题;⑵制定计划;⑶执行计划;⑷回顾。

2.引导探究

师：现在有个实际问题，需要同学们去解决（幻灯片出示例题1）

某花圃用花盆培育某种花苗，经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时，平均单株盈利3元;以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元.要使每盆的盈利

达到10元，每盆应该植多少株？

（学生安静的思考，不一会有几个学生小声的讨论，些许有些争论.）

师：问题解决了吗？

生众：解决了！

师：下面請一位同学说一下自己的解决办法.

生1：可以通过列表格的方式来解决，表格如下：

增加（株）123456

盈利（元）10109740

师：（继续追问）你是怎么想到这个解决方案的？

生1：因为增加的株数是为正整数，而盈利应该是非负数，符合条件的就这几种，从表格上看只要增加1株或2株就可以了，也就是得出结论每盆应该植入4株或5株。

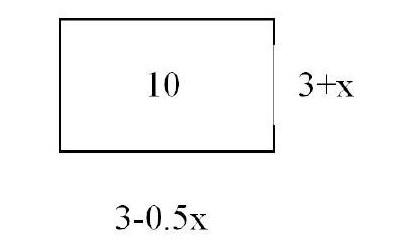
生2：可以把这个题目转化为已知长方形的面积求边长的问题

10=1×10=2×5=4×2.5前面的1，2，4代表可以每盆的株数（取整），后面的因数10，5，2.5代表每盆的利润。根据这个算式可以得出结论每盆应该植入4株或5株。

（课上到这，作为教师的我有点费解，本身不难的题目为什么提问两个学生还没得到我满意的答案，也就是没有用方程的思想来解决这个题目，我只好再提示，一定要出现我想要的形式为止 。）

师：其实这种方法采用的是数形结合的想法，巧妙地把10分成两个数之积的样子，结合题意找出符合条件的答案，其实这个长方形的引入关系不大，还有别的解决方案吗？可否用设元的方式解决呢？

生3：可以设每盆花苗增加x株，则每盆花苗有（3+x）株，平均单株盈利为（3-0.5x）株，由题意可以列如下方程：（3+x）（3-0.5x）=10解出方程即可。

（终于出现我想要的方法了，稍作总结此类题目的解决方法，匆匆的进入下一个环节讲解另外一个例题了。）

二、思考问题，初步诊断

下课之后，再次回想这个教学片段，不禁思考对于此例题学生为什么不喜欢用方程的思想来解决呢？而选择用列算式的方法去运算。与其说不喜欢还不如说不知如何用列一元二次方程的方法去解决。发现此问题不由得让我反思起来，按惯例初二的学生已经适应用方程来解决实际问题，已经可以批量化解决题目，这也变成约定俗成的事情了。问题到底出现在哪？

1.我的教学思路

我看到此例题之后建立如下讲解思路：

（1）先考虑设直接未知数，即设“每盆植x株”，让学生通过尝试发现这样设未知数对表示相关量不方便，因为题设中和各相关量是“每盆花苗增加”的株数，通过上述启发，让学生想到设间接未知数“设每盆花苗增加的株数为x”株。

（2）启发学生用关于x的代数式表示相关的数量，根据等量关系：平均单株盈利x株数=每盆盈利10元，列出方程。

我自认为这是多么好的启发式教学呀。其实大多数老师碰到这个题目都会首选这种方法，因为我们已经被“格式化”了，我们已经变成解题机器了。其实我们也希望自己的学生变成解题机器，现在想想对于初二的学生如果老师在平时的教学中没有充分让学生体会做题目的乐趣，如何能让他们坚持到初三的复习，这也许就是大多数老师讲的初二的学习将会是个分水岭的一个原因所在。

2.学生的解决办法

大部分学生的解法避开方程，而采用枚举法来解决，教学片断中予以体现。（还有一些相类似的解法不在此列举），还有学生用函数的思想来解决，通过画图验证出平均单株盈利是每盆株数的一次函数，由于此法工作量大，就没在班里介绍。

现在想想为什么不花上一节课真的让他们开动脑筋把能想到的方法都深入下去，让他们真正的体会算法多样化的乐趣，只有在平时把这些落实下去，才能避免初三复习的题海战，真正的能作到减负于学生，才能更好的应付千变万化的中考题目。

3.例题的缺点

其实，这个例题老师都清楚，它只不过是披着生活化的外皮实际上是伪生活化的一个题型而已。在教学中学生不领情，这就是原因所在，生活中花农真的是按照这种方式来培育花苗吗？真的是增加7株，就会单株盈利负0.5元吗？显然这不符合生活道理，也无法让学生理解这个例题的生活化。真的要他们做，他们只能在老师的强制下按部就班的用方程的思想解决此题，其实放手让他们自己去解决或许有多数人不会用方程来解决，这个题目其实这个题目就是编者编出来的，学生知道老师也知道，现实生活真的会这样吗？难道这样的培育花苗是生活中存在的吗？这明显是一道伪生活化的题目，放在这无非是引入一类题型，我们需要这样的实际问题来充填这部分知识点。 很多知识都要体现从生活中抽象而来，反过来又作用于生活，其实一定要从生活中来确实难为编者了，生活中没这样的例子，那就编造一个出来，经过加工提炼或者说是伪造的生活情景，从实际教学的情况来看，学生也根本不感兴趣，体现不出数学的应用价值。学生只能体会到这只是做数学题而已，呀. 其实我们老师都清楚这一节课我们就是在传授一个模型。

总利润（费用）=总数量×单个利润（费用）-其它费用

4.例题的复制

有了例1这样的例题，接着来的就是批量生产出一类练习题，比如本节作业题的第一题，题目如下：某超市销售一种饮料，平均每天可售出100箱，每箱利润120元，为了扩大销售，增加利润，超市准备适当降价，据测算，若每箱每降价1元，每天可多售出2箱，如果要使销售饮料获利14000元，每箱应降价多少元？其实做此类应用题时，要明确题目中所给的信息，并找到其中相等的量可以用不同的表达式表示就可以列出方程。这就是编者编写它的理由所在，知道本质所在大家都可以编此类题，只不过是冠上不同的生活情景而已，其实都是大家杜撰的生活化，这是出题目的人和做题目的人都心照不宣的事情了。我们老师也要把学生培养成只要看到此类题就可以把模型找出来，进而设元，找等量关系，再列方程解决它。

这类题型的出现把做数学题目当成了零件的批量生产，到了换个马甲我也认识的地步，其实题目做过之后什么也不会留下，学生就变成了做题目的机器。日以至此，我们的数学变成了什么？数学来源于生活，也必须根植于生活” 。这是每个人教师都会挂在嘴边的一句话，仅是说说而已吗？紧密联系学生的生活实际，让数学从生活中来，到生活中去，学有应用价值的数学是新课程改革的重要理念。仅是读读而已吗？

三、反思问题，再次诊断

中考题换了一个角度来审视此题，给出学生最熟悉的方法——方程解决此题，要求用一种与之不同的方法求解上述问题。这无疑是给我当头一棒。敲醒了我，使我对此题有了更深刻认识。基础知识看似独立，实际上彼此之间的微妙联系需要我们老师给学生去总结去提升，我们要在学生现有知识体系下把一张网呈现给学生，引导学生多角度分析一类问题的实质。这样才能在理性、轻松的学习数学，教师要把基础知识的来龙去脉多方面的展示给学生。就那此题为例，在讲授新课的时候教师要从三方面提炼出此题的解决策略，方法一，列表法（此方法直观形象体现了未知数的变化过程）;方法二，图像法（此方法在一次函数的基础上利用图像直观性把两个变量：株数和单株盈利，体现在直角坐标系，代数问题转化为几何问题）;方法三，方程法（解决实际问题需要最简单的设元法把未知的变换成已知的，借助方程来解决）。其实这里老师还需要一个最优化的讲解，以及这三种方法的联系要引导学生去归纳。这样也為后续的二次函数打下一个大大的伏笔。我们都相信好的老师只应是引路者而非灌输者。

（作者单位：浙江省衢州市实验学校，浙江 衢州 324000）