基于可编程门阵列的四极杆质谱仪数字滤波器的设计与应用
王宁 黄泽建 刘梅英 楚士颖 戴新华 方向 江游 田地


摘 要 引入数字滤波器是提高四极杆质谱仪信噪比的一种有效方法。针对小型四极杆质谱仪控制系统数据处理能力不足的问题, 本研究提出了基于FPGA芯片的数字滤波器解决方案。使用FPGA程序替代通用处理器程序进行数字滤波运算, 提高了仪器控制系统数据处理能力, 实现了高阶数字滤波。在本团队研制的小型四极杆质谱仪中, 使用本方案实现130阶数字滤波, 测试全氟三丁胺标准样品的高频噪声衰减-50 dB以上, 502 Th质谱峰信噪比提升95%, 系统功耗仅增加190 mW, 约占系统总功耗的1.7%, 同时解决了通用处理器执行数字滤波容易丢失数据的问题, 为其它低功耗控制系统完成高性能数据处理提供了设计参考。
关键词 数字滤波器; 现场可编程门阵列; 四极杆质谱仪; 小型化; 信噪比
1 引 言
随着危险化学品与密闭环境现场实时监测等工作需求日益增加[1~4], 仪器的小型化成为四极杆质谱仪发展的一个重要趋势[5~7]。仪器小型化要求体积和功耗减小, 但性能与功能的设计需求并不会降低, 因此, 对控制系统的数据处理能力提出了较高的要求。数字滤波器是一种能有效提高质谱信号信噪比(Signal-to-noise, SNR)的数据处理技术, 常见的数字滤波算法主要有小波分解法、匹配滤波法、高斯二阶导数法和Savitzky-Golay滤波法等[8~11], 其性能依赖于控制系统的运算能力。商业质谱仪器, 如美国Thermo公司的DSQ、TSQ系列四极杆质谱仪、Agilent公司的597x和7000系列四极杆质谱仪等, 都是基于专门的数字信号处理芯片或高性能单片机完成运算[12], 能将复杂的数字数据处理算法通过编程高效实现。但是, 受到通用核心串行指令执行方式的影响, 滤波运算会占用较多的运算资源, 长时间中断进程容易造成系统响应缓慢, 因此, 这种方式的流畅运行依赖于系统配置的高性能核心, 功耗难以降低, 系统结构也难以精简。由通用中央处理器(Central processing unit, CPU)和可编程门阵列(Field programmable gate array, FPGA)组建的控制系统兼备通用性、扩展性与小型化等特点[13~15], 由低功耗CPU进行数据处理运算, FPGA提供硬件电路时序控制。但是, 低功耗CPU的串行计算模式与计算能力难以满足数字滤波器中大量乘法运算需求, 数据处理时会出现数据丢失的问题, 阻碍了质谱数据的高速获取与应用。
根据上述问题, 本研究提出一种基于FPGA的数字滤波器解决方案, 以通用CPU+FPGA为控制系统架构, 在有限的CPU运算能力下, 通过FPGA芯片实现低功耗数字滤波运算, 合理分配系统运算资源, 减小CPU的运算压力, 提高了系统数据处理能力, 在实际应用中取得了满意的效果。
2 实验部分
2.1 小型四极杆质谱仪整机结构
本研究组研制的四极杆质谱仪器结构如图1所示[16]。仪器机械部件主要包括真空腔体、电子轰击电离源、四极杆质量分析器、进样装置和机械泵等部分, 控制系统主要包括小信号采集转换电路、CPU主板、FPGA板和显示设备等。样品通过进样装置进入离子源, 产生的离子通过质量分析装置形成电信号, 由静电计放大器与模拟/数字(Analog/Digital, A转换电路转换成质谱数字信号, 在控制系统的FPGA芯片内对质谱数字信号进行快速数字滤波运算, 结果数据通过PC104总线传输到CPU, 进行谱图解析与显示等操作。
2.2 基于FPGA的数字滤波器设计
实现数字滤波器的FPGA芯片及其控制单元系统结构框图如图2A所示。该芯片采用Intel公司Cyclone IV系列EP4CE30, 具有丰富的逻辑单元、数字乘法器和双端口随机存储器等资源。使用Matlab r2017b(美国MathWorks公司)及Quartus Prime 16.0(美国Intel 公司)等软件联合设计, 实现数字滤波器。
CPU(Vortex86DX 32-bit处理器/主频800 MHz)与FPGA通过PC104总线进行控制信号和数据的传输, FPGA中控制模块负责解析CPU控制指令, 产生同步转换脉冲(PCNVST)启动模拟/数字转换芯片AD7663(美国Analog Device公司)采集, 将质谱模拟电压信号转换为16-bit数字信号; 16-bit串行数据DATA及其同步数据时钟DCLK同时进入FPGA, 由FPGA串并转换程序模塊转换为16-bit并行数字信号, 输出给数字滤波器模块运算并返回CPU系统。基于Verilog HDL硬件描述语言设计的程序流程图如图2B所示。
数字滤波器根据其单位冲激响应可分为有限长单位冲激响应(Finite impulse response, FIR)和无限长单位冲激响应(Infinite impulse response, IIR)两种形式。相比于IIR, FIR形式具有严格线性相位, 信号内不同频率成分间仍保持原始相位差, 只改变信号波形幅值, 质谱信号失真较小。FIR数字滤波算法结构如图3所示, 图中Z-1为离散系统单位延迟, 此处等于模拟/数字转换器采样周期; Cn为滤波器系数矩阵中第n个系数。原始数据经过k级延迟后, 与Ck-1相乘, 再与数据流中Dk-1相加, 形成Dk。若n为滤波器阶数, 经过n+1级延迟后, 输出Dn+1即为运算结果。系统运行时, 连续采集数据, 单次运算在单位延迟内完成, 数据流整体经过n+1级延迟后进入控制系统。以采样周期为间隔, 滤波结果连续产生并返回, 与CPU建立完整的数据流通道。
2.3 数字滤波器参数设计
数据流延迟时间tD和采样周期Ts及滤波器阶数n有如下关系:
tD=Ts×(n-1)(1)
系统设置AD7663采样速率为200 kSPS, 采样周期Ts=5 μs。根据Nyquist定理, 系统带宽为100 kHz。使用MATLAB设计基于Hamming窗函数的FIR滤波器, 截止频率配置范围为0~100 kHz; 滤波器阶数配置范围为1~200阶。质谱信号主要包含低频成分, 采用低通滤波器滤除噪声效果较好。以截止频率2 kHz, 阶数分别为40和130阶为例, 分别绘制滤波器频率响应曲线(图4)。理论阻带最小衰减分别达到-45和-55dB
3 结果与讨论
3.1 质谱数据采集与分析
本系统质量扫描范围为350~550 Th, 扫描速度为400 amu/s, 全氟三丁胺(美国Sigma-Aldrich公司)的蒸气通过流量阀进入电子电离源, 采集得到仪器基线和标准样品质谱图。使用MATLAB分析信号频率特性及统计参数, 仪器基线和标准样品质谱图及频谱图如图5所示。干扰噪声主要由系统及环境噪声和A/D转换产生的量化噪声等随机噪声组成, A/D转换前, 系统硬件设计有截止频率10 kHz的Butterworth低通滤波器滤除部分系统及环境噪声。对比图5B和图5D, 仪器基线和标准样品信号相同频率处出现强度较高的噪声成分, 在模拟滤波器后, 几种噪声成分仍然存在, 进入控制系统, 将对质谱信号产生干扰。由图5C可见, 502 Th质谱峰受到噪声影响, 谱峰抖动明显, 半峰宽等谱峰特征难以识别。
3.2 数字滤波结果与讨论
自行研制的质谱仪的CPU软件滤波是基于Hamming窗设计的16阶低通滤波器, 使用FPGA设计, 实现相同结构的数字滤波器, 同时提高阶数。基线信号滤波前后谱图如图6所示。信号峰峰值(Peak-peak value, Vpp)和标准差(σ)明显减小, 主要噪声频率成分得到显著抑制, 且滤波器阶数越高, 抑制效果越强。与滤波前基线Vpp=7.324 mV和σ=0.9929 mV相比, 滤波器阶数分别为16、40和130阶时, Vpp分别降低20.80%、26.95%和35.02%, σ分别降低34.59%、42.92%和52.80%。根据标准样品质谱图的频谱, 统计主要噪声衰减量如表1所示。1.5 kHz位于滤波器通带内, 衰减较小, 使用FPGA 40阶滤波时, 38.07和54.00 kHz处噪声分别衰减-52.21和-61.04dB; 使用FPGA 130阶滤波时, 分别衰减-59.76和-69.26 dB, 均接近理论衰减指标。
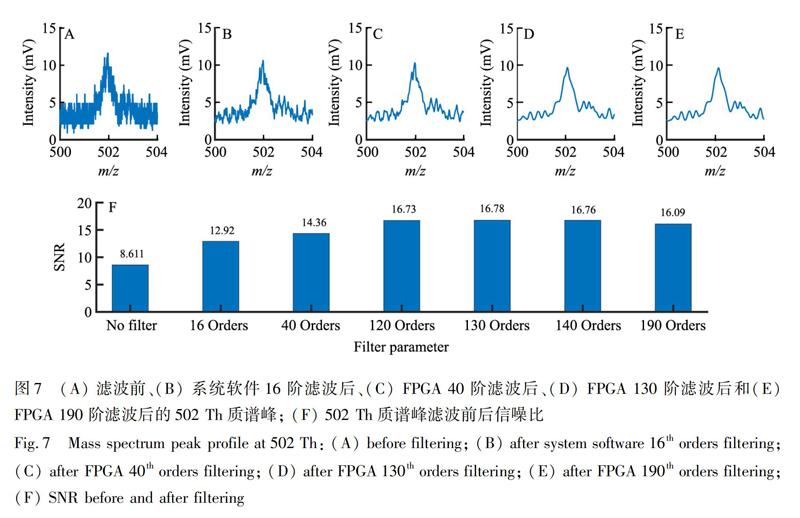
在无滤波、使用系统软件及FPGA滤波502 Th条件下, 谱峰形状及信噪比如图7所示。随着滤波器阶数提高, 谱峰抖动逐渐减少, 滤波后系统软件识别谱峰半峰宽为0.5 amu, 且谱峰信噪比明显提升。在130阶附近达到信噪比顶峰, 130阶以上时, 谱峰形状与信噪比无明显改善。
对于本研究设计的40阶和130阶滤波器, 目标频率理论衰减量与衰减量误差如表2所示, 对应频率点实际衰减量与理论衰减量均存在一定误差。由于滤波器系数是使用MATLAB软件设计生成的双精度浮点数, 而 EP4CE30仅支持整型数的数字滤波, 因此需要将系数量化, 且量化位数决定了系数加载精度。由于浮点数量化为二进制数, 必然会引入误差, 从而导致滤波器的实际频响曲线与理论曲线相比存在畸变, 因此, 理论与实际衰减倍数存在一定误差。其中, 38.07 kHz在130阶滤波器的频率响应曲线中位于波谷处, 附近曲线变化率较大, 相同频率誤差在此处会造成更大的衰减量变化, 因此, 使用130阶滤波器时, 38.07 kHz处衰减量误差比其余情况下更大。通过提高滤波器系数量化位数可以提高实际频率响应曲线与理论曲线的匹配程度, 进而缩小理论与实际滤波效果之间的误差。但是, 提高量化位数也会相应增加系统运算资源的消耗, 因此, 实际设计过程中, 应根据系统资源与性能需求进行权衡。
由系统软件运行的40阶和130阶滤波器延迟时间分别为60~70 ms和120~130 ms, 软件滤波延迟为非线性增加, 具体情况与软件及操作系统的中断运行机制和子程序调用有关, 在此处不做详细讨论。本研究设计的数字滤波器延迟时间与系统时钟频率和滤波器阶数有关, 在系统时钟频率固定的情况下, 延迟时间与滤波器阶数成正相关。40阶和130阶滤波器理论延迟分别为200和650 μs, 远小于系统软件滤波时间。并且, 由于FPGA采用时序逻辑输出, 逻辑电平建立时间为ns级别, 因此对实际延迟时间造成的误差很小。根据本研究中数字滤波器的结构, 延迟时间内质谱数据未完成滤波运算, 期间的输出结果表现为从0逐渐增加至真实值, 此过程所需时间恰等于延迟时间。为正确获取谱图数据, 应剔除延迟时间内的无效数据, 消除由延迟引起的谱图整体偏移。
通过实际测试, 根据本研究方法改进控制系统, 使用FPGA实现130阶滤波器, FPGA逻辑单元增加434个, 约占资源总量的1.5%。滤波前, 系统功耗为11.79 W; 开启滤波后, 系统功耗为11.98 W, 仅增加约190 mW, 约占控制系统功耗的1.7%, 且系统连续稳定运行1000 h以上。
4 结 论
设计了一种基于FPGA的FIR数字滤波器, 应用于四极杆质谱仪, 相比CPU软件滤波方式, 以较少的系统资源实现运算性能大幅提升, 并且实现了100阶以上的滤波, 显著提高了谱峰信噪比, 同时满足小型仪器控制系统的性能及指标要求, 有利于推动四极杆质谱仪小型化进程。
References
1 Li L F, Chen T C, Ren Y, Hendricks P I, Cooks R G, Ouyang Z. Anal. Chem., 2014, 86(6): 2909-2916
2 Peris-Díaz M D, Sentandreu M A, Sentandreu E. Anal. Bioanal. Chem., 2018, 410(7): 1-10
3 Zhang X T, Hou H W, Chen H, Liu Y, Wang A, Hu Q Y. Biomed. Chromatogr., 2018, 32(9): e4181
4 Gethings L A, Richardson K, Wildgoose J, Lennon S, Jarvis S, Bevan C L, Vissers J P C, Langridge J I. Rapid Commun. Mass Spectrom., 2017, 31(10): 1599-1606
5 HUANG Ze-Jian, LIU Guang-Cai, JIANG You, LIU Mei-Ying, PIAO Yi-Qing, GONG Xiao-Yun, ZHAI Rui, XIE Jie, DAI Xin-Hua, FANG Xiang. Chinese J. Anal. Chem., 2019, 47(7): 985-991
黄泽建, 刘广才, 江 游, 刘梅英, 朴怡情, 龚晓云, 翟 睿, 谢 洁, 戴新华, 方 向. 分析化学, 2019, 47(7): 985-991
6 FU Qing, YOU Xiao-Ming, JIN Jie. Journal of Chinese Mass Spectrometry Society, 2019, 40(3): 259-267
富 庆, 尤晓明, 金 洁. 质谱学报, 2019, 40(3): 259-267
7 YANG Xian-Wei, PAN Li-Qing, WANG Jin-Dong, LUO Zhi-Hui, TAN Chao, ZHAO Hua. Journal of Chinese Mass Spectrometry Society, 2016, 37(3): 247-254
杨先卫, 潘礼庆, 王劲东, 罗志会, 谭 超, 赵 华. 质谱学报, 2016, 37(3): 247-254
8 Penedo S R M, Netto M L, Justo J F. Eurasip J. Adv. Signal Process., 2019, (1): 33
9 ZHANG Xing-Xing, LU Ji-Cheng, LI Xia-Yu, YU Jun. Microelectronics, 2018, 48: 429-432
张幸幸, 陆继承, 李夏禹, 俞 军. 微电子学, 2018, 48: 429-432
10 Fredriksson M, Petersson P, Jrntén-Karlsson M, Axelsson B O, Bylund D. J. Chromatogr. A, 2007, 1172(2): 135-150
11 Qi Y L, Li H L, Wills R H, Perez-Hurtado P, Yu X, Kilgour D P A, Barrow M P, Lin C, OConnor P B. J. Am. Soc. Mass Spectrom., 2013, 24(6): 828-834
12 Yang T. Proc. SPIE-Int. Soc. Opt. Eng., 2011, 8001(2) : 162
13 Gao Y H, Zhou J, Wang W, Wu B J. Appl. Mech. Mater., 2012, 239-240: 901-904
14 JIANG You, WU Bao-Jun, RANG Yu, TIAN Di, FANG Xiang. Journal of Chinese Mass Spectrometry Society, 2008, 29(2): 65-69
江 游, 吳保军, 穰 瑜, 田 地, 方 向. 质谱学报, 2008, 29(2): 65-69
15 Snyder D T, Pulliam C J, Ouyang Z, Cooks R G. Anal. Chem., 2016, 88(1): 2-29
16 LIU Guang-Cai, GONG Xiao-Yun, JIANG You, PIAO Yi-Qing, FANG Xiang, HUANG Ze-Jian, TIAN Di. Chinese J. Anal. Chem., 2019, 47(5): 686-694
刘广才, 龚晓云, 江 游, 朴怡情, 方 向, 黄泽建, 田 地. 分析化学, 2019, 47(5): 686-694
Design and Application of Digital Filter for Quadrupole
Mass Spectrometer Based on Field Programmable Gate Array
WANG Ning1,2, HUANG Ze-Jian2, LIU Mei-Ying2, CHU Shi-Ying2, DAI Xin-Hua2,
FANG Xiang2, JIANG You*2, TIAN Di*1
1(College of Instrumentation & Electrical Engineering, Jilin University, Changchun 130061, China)
2(Mass Spectrometry Engineering Technology Research Center, Center for Advanced Measurement Science,
National Institute of Metrology, Beijing 100029, China)
Abstract Digital filtering is one of the most important methods to improve the signal-to-noise ratio of quadrupole mass spectrometer. Aiming at the insufficient data processing capacity of the control system in miniature quadrupole mass spectrometers, one solution of digital filtering which based on FPGA was proposed in this work. The FPGA program instead of the general processor program was used to perform digital filtering operations, which improved the data processing capability of the instrument control system and completed high-order digital filtering. In miniature quadrupole mass spectrometer developed by our team, the solution here was used to achieve 130-order digital filtering. The high frequency noise attenuation of the perfluorotributylamine standard sample was more than -50 dB. The power consumption was only increased about 190 mW, which accounted for about 1.7% of the total power consumption of the control system. Meanwhile, it solved the problem of easy data loss caused by general processors for digital filtering, and provided design reference for other low-power control systems to complete high-performance data processing.
Keywords Digital filter; Field programmable gate array; Quadrupole mass spectrometer; Miniature; Signal-to-noise ratio
(Received 13 December 2019; accepted 27 May 2020)
This work was supported by the National Key Research and Development Plan of China (Nos. 2018YFF0212503, 2011YQ090005).
2019-12-13收稿; 2020-05-27接受
本文系国家重点研发计划项目 (Nos. 2018YFF0212503, 2011YQ090005)資助
* E-mail: jiangyou@nim.ac.cn; tiandi@jlu.edu.cn

