双通道闭环步进电机控制器设计*
段长超,刘青正,韩震宇,方 辉
(四川大学 机械工程学院,四川 成都 610065)
0 引 言
在大跨度龙门铣床、激光切割机床等设备中,工作台和龙门横梁等大跨度运动部件常采用两套相同的伺服驱动装置,进行单轴双电机对称同步驱动[1-2]。该方式需严格保证两套伺服驱动装置的响应性能一致,实现难度和成本均较高。而双通道电机驱动装置则能以较低的成本,实现机床的单轴双电机同步驱动。
然而,目前的双通道电机驱动装置,如多输出的开环步进电机驱动器[3-4]、双通道交流伺服驱动器[5-6]、双通道直流驱动器[7]等通用型开环或伺服驱动装置中,不具备闭环接口或双通道为独立驱动输出,驱动器无法直接调节双通道输出的同步偏差,因此其驱动控制性能将受到被驱动对象结构参数、摩擦系数和阻尼系数等参数一致性的限制。
笔者面向数控应用,开发一套功能独立的经济型双通道闭环步进电机控制器,并紧密结合数控系统原理设计其软、硬件架构,采用双通道耦合调节算法调节双通道输出同步偏差[8-10],且控制器能同时实现三闭环控制,其能参与构建更高运行效率的新型数控系统。
1 系统整体分析
数控系统架构如图1所示。

图1 数控系统架构
伺服驱动器是闭环数控机床的关键组成部分,其性能决定了数控机床的加工性能[11-12]。在传统的闭环数控架构中,位置闭环由上位计算机的位置调节器实现,速度环和电流环由伺服驱动装置实现,系统的运行效率主要受限于系统插补周期、采样周期以及伺服驱动装置的响应性能。
新型数控架构中,伺服驱动装置接收上位机按插补周期定时下发的插补微位移指令,并同时实现三闭环调节,因此,双通道伺服驱动装置应具备位移和速度检测接口各两路。新数控架构中在插补计算精度足够的前提下,数控系统性能只受限于伺服驱动装置的响应性能,因此大大简化了闭环数控系统架构,同时也可大大缩短系统插补周期,提高系统运行效率,但同时也对伺服驱动装置提出了更高的要求。
数控系统中,上位机下发的指令包括微位移指令(1个插补周期内的位移增量)和长位移指令(多个插补周期内的总位移增量)。微位移指令需由伺服驱动装置按系统插补周期转化为理论应发脉冲数和理论捕获脉冲数,并实现位置闭环调节。长位移指令则需由伺服驱动装置先进行速度规划,并按系统插补周期实现位置闭环调节。该系统中上位机下发指令的接收、转换和速度规划均由STM32实现,双通道控制脉冲发送和闭环采样均由FPGA实现。
传统双通道伺服驱动装置中,双通道单独实现速度环和电流环双闭环,双通道输出之间的同步误差无法直接调节。该系统共包含双通道位置环、速度环共4个PID控制器,并采用改进的PID闭环调节架构以消除双通道速度环和位置环的同步偏差。
2 系统硬件设计
运动控制器控制模块硬件架构如图2所示。
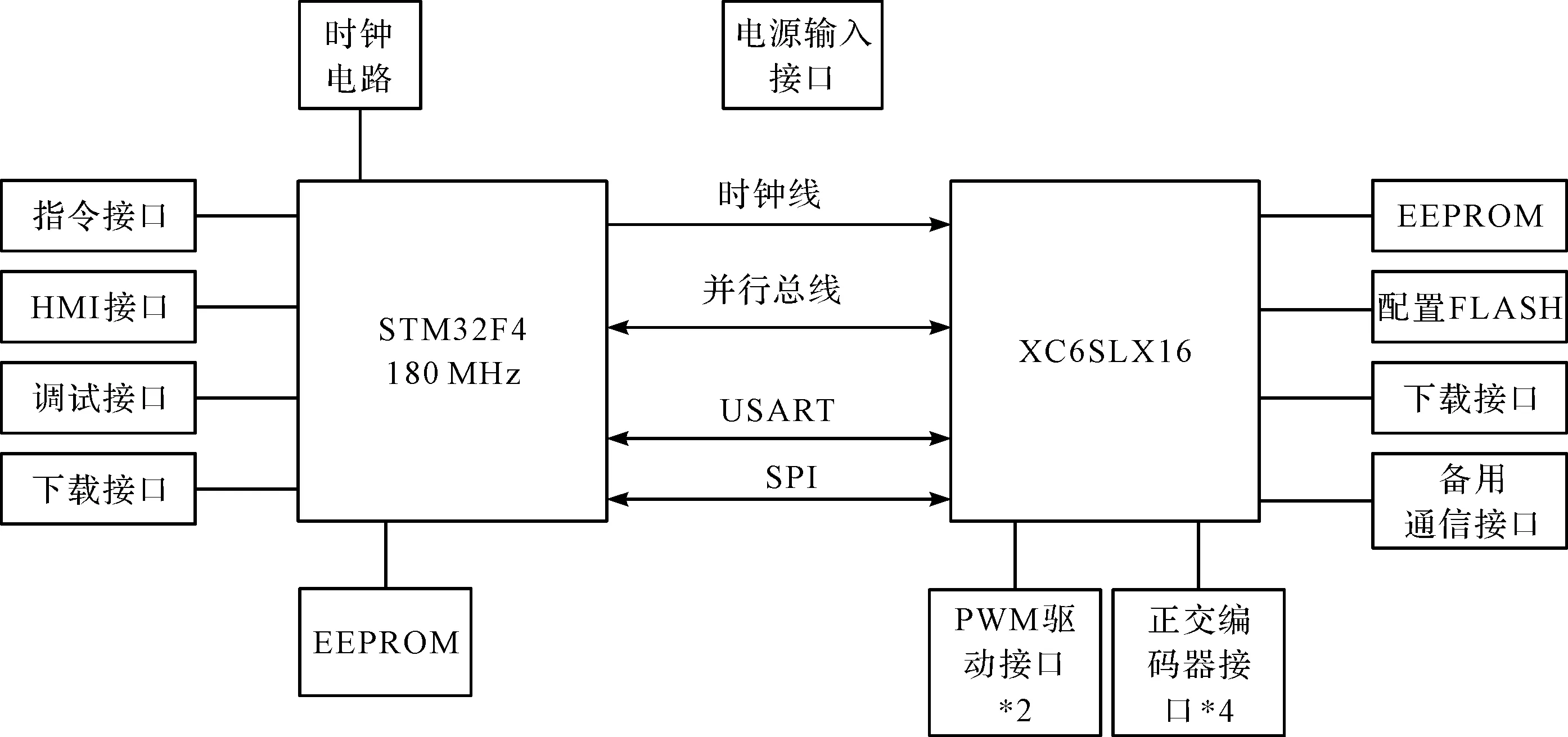
图2 控制模块硬件架构
图2中,采用“STM32+FPGA”的硬件架构,STM32通过指令接口接收外部系统下发的微位移或长位移指令,将微位移指令转化为单位插补周期内的应发脉冲数和应捕获脉冲数,并按插补周期发送给FPGA执行;或将长位移指令按插补周期进行速度规划和数据转化,并按插补周期发送给FPGA执行。FPGA接收STM32下发的指令并按系统插补周期发送控制脉冲、采样并实现速度环和位置环双闭环调节。
此外,HMI接口用于系统状态监视、EEPROM为系统状态参数存储、16位并行数据总线为指令下发总线、SPI和USART总线为FPGA状态数据上传总线、PWM驱动接口输出双通道步进电机控制信号至驱动模块、正交编码器接口捕获编码器和光栅尺信号。
驱动模块架构如图3所示。
图3中,驱动模块实现系统电源和步进电机驱动电路。驱动电路采用2片集成驱动芯片THB8128,控制信号输入接口接收控制模块输出的控制信号,电源输入接口为系统总电源36 VDC输入,稳压芯片LM2596转换后的各电源通过电源输出接口输出至控制模块。
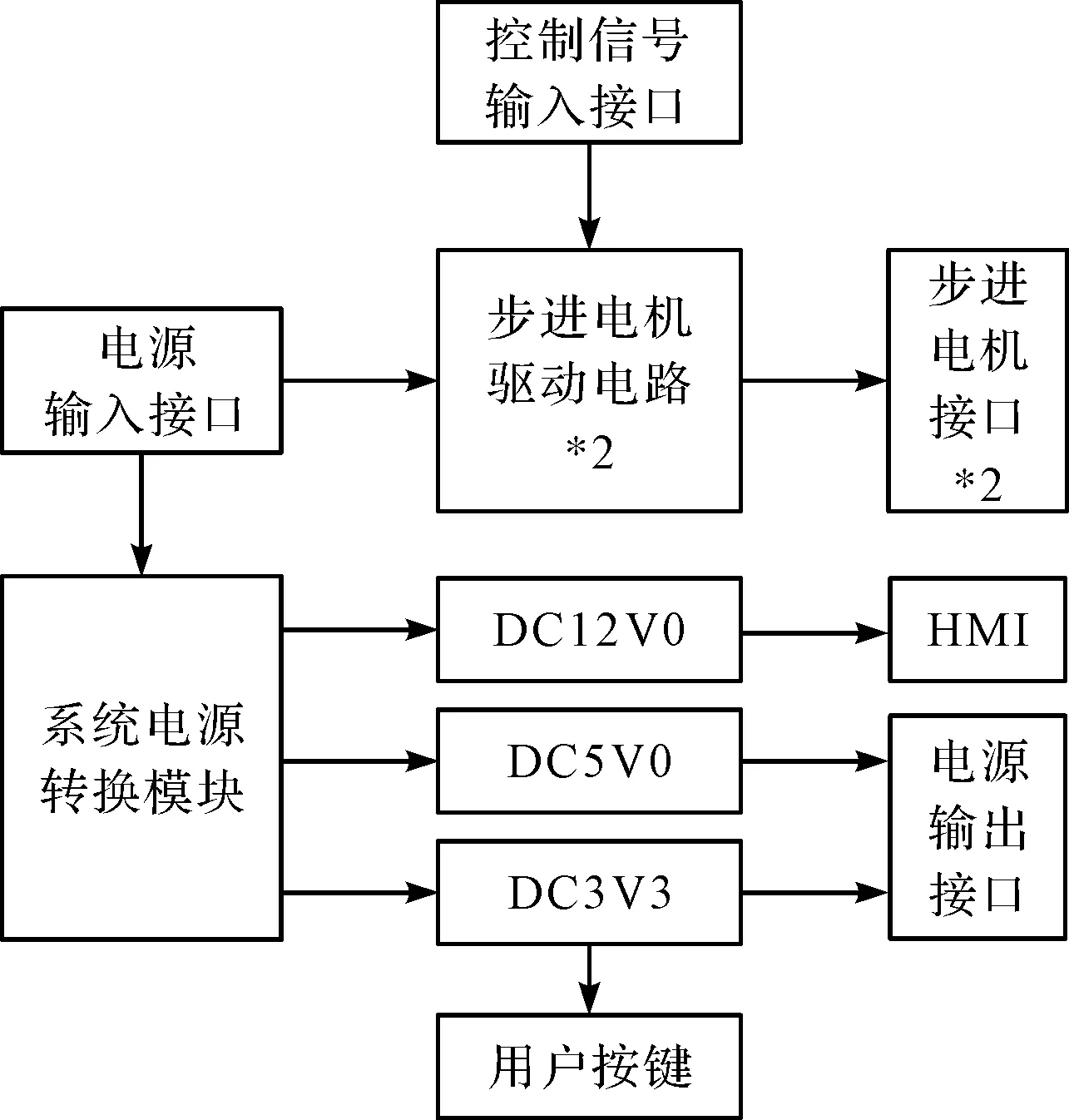
图3 驱动模块架构
3 双通道闭环同步控制算法
双通道闭环同步控制算法结构框图如图4所示。
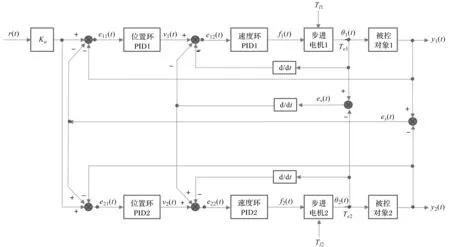
图4 双通道闭环同步控制算法结构框图
在双通道闭环步进电机驱动系统中,两步进电机并行通道的位置环和速度环为典型的PID闭环调节架构[13-17],两位置环并行接收相同的外部指令并独立执行。根据步进电机的矩频特性,系统采用“减速同步”策略调节双通道的同步偏差,即以增大扭矩而非速度的方式实现双通道同步。
该系统中,被控对象的位移执行偏差es(t)=y1(t)-y2(t),其与位置同步系数Kss的乘积作用于两位置环PID控制器。需要注意的是,同一位置环调节周期内该同步偏差调节项仅作用于两位置环PID控制器之一,选择的依据为:es(t)>0时,es(t)负反馈到位置环PID控制器1;当es(t)<0时,es(t)正反馈到位置环PID控制器2。速度环同步偏差调节的原理类似。
该运动控制器两通道位置环PID控制器的增量控制算式如下:
(1)
(2)
(3)
式中:e(k)—位置环偏差;es(k)—双通道位置同步偏差;Kss—位置同步系数;e0,e1,e2—PID调节项、积分调节项和同步偏差调节项的阈值系数。
如果偏差不超过阈值范围则对应项不参与PID闭环调节,避免位置环振荡。同理,该系统中速度环PID控制器的增量控制算式为:
(4)
式中:e(k)—速度环偏差;ev(k)—双通道速度同步偏差;Ksv—速度同步系数;e0,e1,e2—PID调节、积分调节项和同步偏差调节项的阈值系数。
如果偏差不超过阈值范围,则对应项不参与PID闭环调节。
4 实验结果
笔者搭建了典型的“双边驱动”实验平台,其横梁(工作台)在X轴向的运动由两路步进电机左右对称同步驱动,两路步进电机由一套双通道步进电机驱动器驱动。其中,所用电机为57HB250-80B两相混合式步进电机,额定电流4.5 A,采用细分驱动,机械步距角1.8°;电机编码器为1 000线正交编码器;光栅尺型号KA300-1020,分辨率5 μm,有效行程1 020 mm,输出信号类型为TTL型正交编码器信号;实验载荷重17 kg;丝杠导程10 mm。
设定系统位置环和速度环采样周期分别为4 ms、2 ms,STM32的指令下发周期为8 ms。分别在空载、带固定载荷(质量和Y轴位置均固定)和变载工况(质量不变、Y轴位置变化)下,以不同的指令速度运行5 s(长位移指令),以测定系统的定位误差和位移同步误差。其中,变载工况中载荷在Y轴方向上的来回移动速度为30 mm/s,定位误差为双通道位移输出与指令位移的偏差值的较大者。
在空载、带载和变载3种工况下,运动控制器最终定位误差测试结果如表1所示。

表1 运动控制器最终定位误差测试结果
从表1中测试结果可看出:无论在空载、带载还是变载工况中,各指令下的实测位移均与理想参考轨迹完美重合。实测数据表明,随着指令速度的增大,指令执行的最终定位误差总体上呈增大趋势。空载和带固定载荷工况下执行35 mm/s以下的指令速度时,运动控制器的最终定位误差均低于0.075 mm。在变载工况下,指令速度达到30 mm/s时,所测得的部分数据显示最终定位误差超出0.08 mm,可见在载荷大幅变动的情况下,该控制器在30 mm/s的指令速度以内运行为最佳。值得强调的是,各速度指令下的位移曲线起点并未从时间轴的零点开始,而延迟了约0.15 s,该延迟时间主要由STM32的速度规划延时引起,若控制器执行微位移指令,则不会存在该延时。
3种工况下的同步误差测试曲线如图(5~7)所示。

图5 空载工况同步误差测试曲线
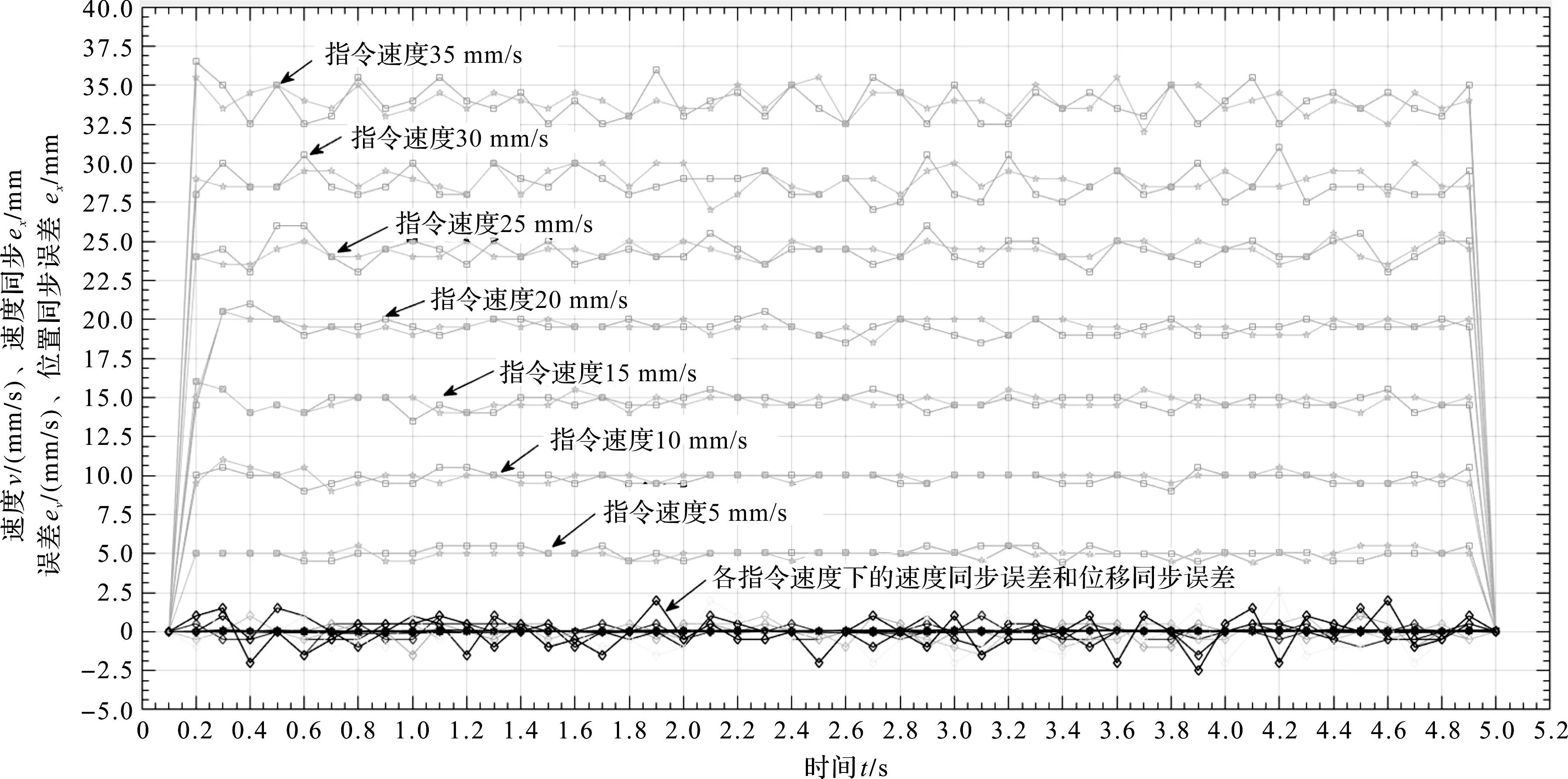
图6 带载工况同步误差测试曲线

图7 变载工况同步误差测试曲线
运动控制器同步误差测试结果如表2所示。

表2 运动控制器同步误差测试结果
从实测结果来看,双通道最大位移同步误差和最终位移同步误差总体上随着指令速度的增大而增大,指令速度在35 mm/s以下时,最大同步误差最大值为0.095 mm,最终同步误差最大值为0.085 mm。
同时,在空载、带载和变载工况下执行相同的速度指令时,双通道位移同步误差无明显的递增或递减规律,可知载荷对该系统的双通道位移同步误差影响不大,可见所采用的双通道同步控制策略的有效性。
以45 mm/s指令速度和不同的加减速度参数运行2 s。
带载工况下的加减速性能测试曲线如图8所示。
从图8中可看出,实验测试中的最小加速时间为0.05 s,双步进电机均出现上超调并迅速返回指令速度曲线附近波动。
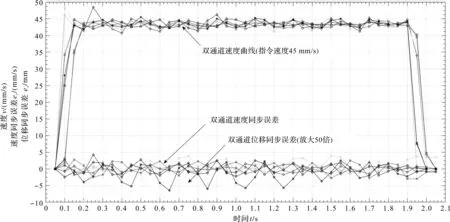
图8 带载工况下的加减速性能测试曲线
在测试的所有数据中,双步进电机的位置定位误差和位置同步误差均保持在0~0.095 mm范围内,系统运行流畅,且无任何卡顿现象。
5 结束语
笔者设计的双通道闭环步进电机运动控制器面向数控系统,能同时实现闭环数控系统三闭环;实验数据显示,控制器在35 mm/s的指令速度范围内,在空载、带固定载荷、变动载荷工况下,双通道最终定位误差最大值和同步误差最大值分别为0.055 mm和0.065 mm、0.075 mm和0.065 mm、0.085 mm和0.085 mm。实验结果表明:在带载工况下,系统加减速度也能达到900 mm/s2以上,且能同时满足系统定位和同步精度要求。
该步进电机运动控制器实现了研究初期的功能和性能要求,有利于提高新架构数控系统的运行效率。
值得强调的是,测试实验中所设定的PID参数并不一定是最优化的,要进一步提升控制器的运行性能,除采用更高分辨率的速度和位置检测元件外,系统中各闭环PID控制器的参数有待实现自整定,这将是后期研究的重点。

