金红石辐照损伤的分子动力学模拟

吴晓华，王 刚，李伟民

1.绵阳市聚合新材料有限公司，四川 绵阳 621025；2.西南科技大学 核废物与环境安全国防重点学科实验室，四川 绵阳 621010

核能开发和应用的同时会产生大量的放射性废物。这些放射性废物对所有生命形式和环境均有害，需要与生物圈永久隔离。低水平和一些中等水平放射性废物需要储存在近地表处置库中数百年，而高放射性废物(HLW)，由于它们漫长的半衰期必须深埋在高放射性废物处置库中数万年。对于高放废物一个可行的方案是将它们固基材化在玻璃或陶瓷基材中，然后长期贮存在高放射性废物处置库中。Ringwood等[1]提出了一种名为SYNROC的合成岩石作为固化HLW的多相材料。 SYNROC主要由三种钛酸盐材料(钙钛锆石、钙钛矿和碱硬锰矿)、金红石和少量合金相组成。二氧化钛主要有金红石、锐钛矿和板钛矿三种晶型。金红石作为宽带隙半导体，已被广泛用于光催化[2-4]和稀磁半导体[5-6]。金红石具有四方结构(P42/mnm空间群)，晶胞参数a=b=0.459 4 nm，c=0.295 9 nm[7]。

离位阈能(threshold displacement energy，TDE)是将原子从其原始晶格位置移位到缺陷位置的最小能量，这对于估计材料的辐射耐受性至关重要[8-9]。早期Buck等[10]使用高压电子显微镜(HVEM)和透射电子显微镜(TEM)获得了金红石的TDE值。结果表明，Ti的TDE为45～50 eV，O的TDE为33 eV。Smith等[11]使用时间分辨阴极发光光谱(TRCS)确定了金红石中O的TDE为(39±4) eV。

分子动力学(MD)模拟的应用可以更好地理解辐射损伤的机理。 Richardson[12]最初计算了金红石的TDE值，结果显示Ti的TDE≈50 eV，O的TDE≈10～40 eV。在晶体中，TDE值与初级击出原子(primary knock-on atom，PKA)的离位方向有关，不同离位方向的TDE值不同。TDE最小值表示在所有选择方向上离位能的最小值，而TDE平均值则表示所有方向离位能的平均值。为了对不同晶体学方向的TDE值进行统计分析，Thomas等[13]将TDE定义为缺陷形成概率(defect formation probability，DFP)的函数。随后Robinson等[14]给出了拟合函数：

(1)

其中：α和β是拟合参数；E是PKA能量。使用这个拟合函数Robinson等[14]得到的Ti的TDE≈69 eV，金红石中O的TDE为19 eV。Ti的结果与实验数据吻合良好，但O的TDE值明显低于实验数据和模拟数据。

近几十年来，对高能粒子辐照引起的材料辐射损伤的研究受到了广泛关注。其中一个主要原因是它可以在短时间内达到相当于辐射几年甚至几十年的损伤剂量，这对于模拟辐射损伤非常有吸引力。然而高能粒子辐照实验无法通过辐照时间观察到缺陷类型和数量的信息，也无法观察缺陷的分布状态。本工作拟采用分子动力学(MD)模拟来评估缺陷的产生和演变：首先在300 K下，计算266个不同方向上金红石的Ti和O原子的TDE值，然后模拟Ti和O在10 keV的能量下反冲产生的位移级联。

1 模拟方法

分子动力学模拟采用LAMMPS软件[15]，Ti-O、Ti-Ti和O-O原子总相互作用势(Φ(rij))采用公式(2)计算。

(2)

其中：ΦZBL(rij)，ZBL(Ziegler-Biersack-Littmark)屏蔽库仑势[16]；ΦS(rij)，五阶样条函数；ΦBUCK(rij)，Buckingham短程相互作用[17]；ΦCOUL(rij)表示长程库伦相互作用。本工作中ra和rb分别选取0.6 Å和2.0 Å(1 Å=0.1 nm)，金红石的Buckingham势函数由GULP软件拟合[18]，O和Ti原子的固定部分电荷分别采用-1.098和2.196。本工作所用到的短程相互作用力为Buckingham形式(式(3))。

(3)

式中：A、ρ、C均为待定势参数，需要拟合得到；A与离子的刚度有关，eV；ρ与离子的尺寸大小相关，nm；C与体系的范德华力相关，eV·nm6。金红石TDE的计算使用具有周期性边界条件的9 000个原子(10×10×15个单位晶胞)的超晶胞，在球面坐标系中选择266个方向作为PKA的离位方向(图1)。位移级联的模拟选取5 760 000个原子(80×80×150个单位晶胞)的超晶胞，VORONOI缺陷分析方法用于识别缺陷类型和点缺陷量。

(a)——球坐标系示意图，(b)——球坐标系下选取的离位方向图1 球坐标系下选取的266个初始离位方向Fig.1 266 PKA directions for calculating TDEs

2 模拟结果与分析

以Isaak等[19]实验测试得到的金红石弹性常数(C11、C33、C44、C66、C12和C13金红石为四方晶系，根据对称性原则，一共存在6个弹性常数)、体模量(B)和剪切模量(G)作为参考值，通过GULP软件包对Buckingham势函数的A、ρ、C参数进行拟合，拟合后的参数值列入表1。由拟合得到的A、ρ、C参数可以计算得到金红石的弹性常数、体模量和剪切模量数值，结果列入表2。由表2可知，通过本工作拟合的Buckingham势函数参数值计算得出的力学性能常数与文献值较为吻合，能够较好地表征金红石的力学性能。

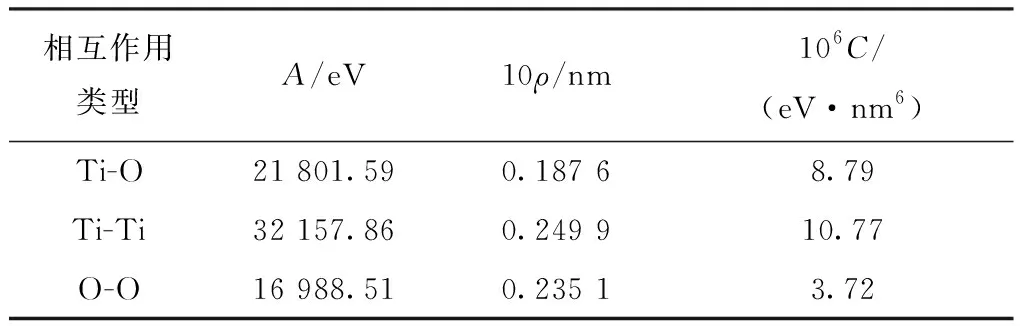
表1 Buckingham势函数拟合结果Table 1 Fitting potential parameters used in present work

表2 金红石弹性常数、体模量和剪切模量计算值与实验值Table 2 Fitting elastic constant(Cij), bulk modulus(B) and shear modulus(G) for rutile with calculated and experimental results

按照公式(1)，金红石中Ti和O原子的DFP拟合结果示于图2。由图2可知：Ti原子的TDE为(78.3±1.0) eV，α和β分别为0.95和99.72；O原子TDE为(42.6±2.0) eV，α和β分别为0.11和0.20。理论上，DFP在0和100%的值应为各出射方向的最小值和最大值，然而公式(1)无法精确地拟合所有数据值，其主要目的是拟合出精确的TDE值[14]。根据模拟结果，Ti和O原子的TDE最小值分别为53 eV和31 eV，TDE最大值分别为294 eV和238 eV，这些最小和最大值严重偏离了曲线的整体趋势，其出现概率较小，并不能代表大多数原子的整体特征。因此本工作在拟合时仅选取了DFP在0～80%的数值。

●——Ti，▼——O图2 Ti和O原子的缺陷形成概率Fig.2 Defect formation probabilities for both Ti and O PKA

由图2还可知，O原子拟合后的TDE为(42.6±2.0) eV，这一拟合结果与前人[10-12]拟合结果吻合较好(30～50 eV)。Ti原子拟合后的TDE为(78.3±1.0) eV，这一结果略高于实验和模拟计算值(45～69 eV)[10，14]。当DFP为10%时，Ti和O原子的TDE分别为91.6 eV和47.9 eV；DFP为50%时，Ti和O原子的TDE分别为145.9 eV和75.4 eV。这一模拟结果与Thomas[13]和Robinson等[14]的结果非常吻合。

在10 keV、300 K下Ti PKA和O PKA缺陷数量随辐照时间的演化示于图3。由图3可知，点缺陷数量随辐照时间演化关系显示了2个趋势：(1) 空位、填隙和不同类型反位缺陷(如O原子填隙缺陷(IO)、O原子空位缺陷(VO)、Ti原子填隙缺陷(ITi)、Ti原子空位缺陷(VTi)、Ti原子占据O原子位置后形成的反位缺陷(TiO)、O原子占据Ti原子位置后形成的反位缺陷(OTi))的数量随辐照时间增加而增加，在辐照时间为0.2～0.3 ps内缺陷数量达到最大值，此时缺陷数量ITi≈VTi>IO≈VO>TiO≈OTi，在随后驰豫阶段，由于缺陷复合作用这些缺陷数量逐渐减少，并且在10 ps左右达到平衡；(2) 同种类型反位缺陷(Ti原子占据另外一个Ti原子位置形成的缺陷(TiTi)和O原子占据另外一个O原子位置形成的缺陷(OO))数量随时间演化展现了不同的趋势，TiTi缺陷数量随辐照时间增加而增加，在10 ps左右达到平衡，而OO缺陷数量随辐照时间增加而增加，但是在辐照时间达到24.4 ps时仍未达到平衡，这说明金红石中O原子的平衡是一个极其漫长的过程。

模拟结束时不同类型缺陷的数量列入表3。由表3可知：不同类型反位缺陷TiO和OTi数量最少，主要是因为这种类型缺陷不稳定，在驰豫阶段逐渐转变为其他类型缺陷。而同种类型反位缺陷数量最多，以Ti PKA为例，TiTi和OO数量之和占总缺陷数量的89%左右，这说明Ti和O原子在被辐照时虽然离开了初始位置，但大部分的原子被驰豫到了其他的Ti和O原子晶格位置，这种类型的缺陷并不会影响基体的性能，所以推测金红石在被辐照后具有较强的恢复能力。出现这一现象的主要原因是空位-填隙的复合作用，如IO+VO→OO和ITi+VTi→TiTi。

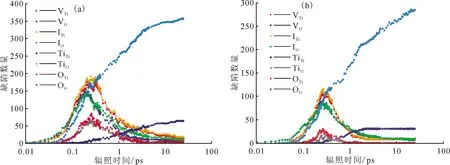
图3 Ti PKA(a)和O PKA(b)缺陷数量随辐照时间的演化Fig.3 Irradiation time dependence of point defect numbers in cascade simulation by Ti(a) and O(b) PKA

表3 模拟结束时不同类型缺陷的数量Table 3 Number of different types of defects at the end of the simulation

Ti原子作为PKA时，在模拟结束阶段(24.4 ps)Ti弗兰克尔缺陷对(VTi和ITi)数量(约为15个)要比最大无序阶段(0.2～0.3 ps)的Ti弗兰克尔缺陷对的数量(约为170～180个)少得多。原因是在驰豫阶段，小部分的Ti填隙进入到了Ti空位形成了TiTi缺陷，而大部分的Ti填隙返回到了原始的晶格位置。与之相反的是，大部分的O填隙进入到了其他的O空位位置形成了数量巨大的OO缺陷，这可能是因为OO缺陷比TiTi缺陷更容易形成，所以导致OO缺陷的数量比TiTi缺陷多。Ti和O弗兰克尔缺陷对的复合在金红石中非常重要，因为它提供了降低间隙和空位浓度的直接机制，可以减少辐照下材料的无序性并提高耐辐照损伤性。同时注意到，TiO和OTi数量几乎为零，这是由于kick-out机制(ITi+OTi→TiTi+IO和IO+TiO→OO+ITi)导致了TiO和OTi缺陷数量减少。

模拟结束时(24.4 ps)，Ti PKA和O PKA的位移原子分布和缺陷类型分布示于图4。从图4可知：Ti原子作为PKA时引起的原子位移和缺陷分布较为密集，具有较强的破坏性；O原子作为PKA时引起的原子位移和缺陷分布较为分散，具有较强的穿透性。且无论Ti原子或是O原子作为PKA时，都会引起大量的原子发生位移，在模拟初期时形成了数量较多的空位缺陷，而在模拟结束时空位数量却非常少，主要原因是在驰豫阶段大量填隙原子通过空位-填隙复合作用填充空位，从而导致空位数量急剧减少。因此，这种空位-填隙复合作用是促使金红石在经受辐照损伤后能够自我修复的主要原因之一。

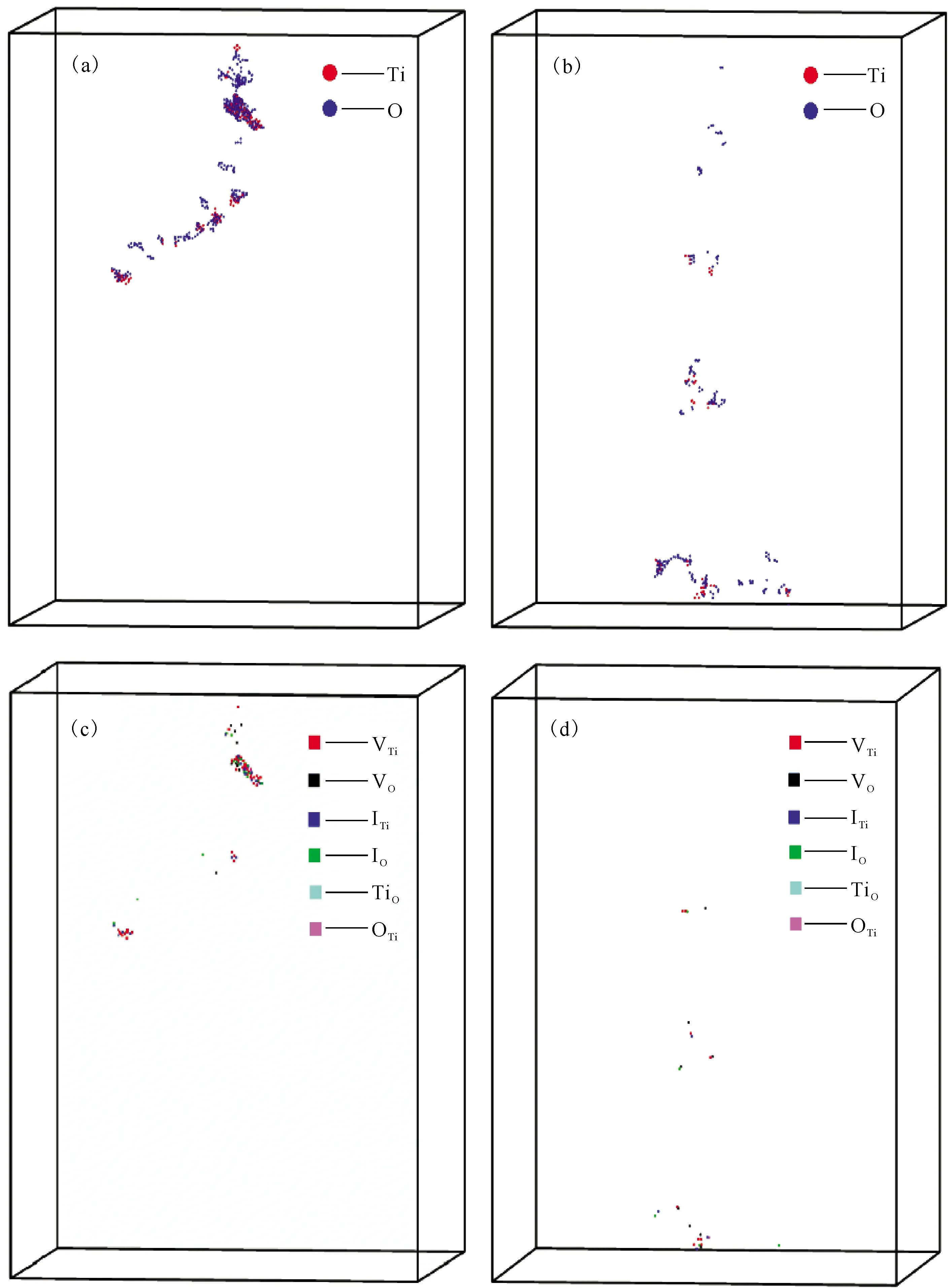
图4 模拟结束(24.4 ps)时，Ti PKA(a)和O PKA(b)引起的位移原子分布以及Ti PKA(c)和O PKA(d)引起的缺陷分布Fig.4 At the end of simulation (24.4 ps), distribution of displacement atoms caused by Ti PKA(a) and O PKA(b), distribution of defects caused by Ti PKA(c) and O PKA(d)

3 结 论

金红石作为固化高放废物的合成岩石成分之一，其耐辐照损伤性能至关重要。采用分子动力学方法研究了金红石的缺陷形成概率(DFP)，计算出了Ti和O原子离位阈能的数值和10 keV能量下缺陷数量随时间演变信息。Ti和O原子的离位阈能值分别为(78.3±1.0) eV和(42.6±2.0) eV。辐照开始阶段，空位、填隙和不同类型反位缺陷的数量随辐照时间增加而增加，在0.2～0.3 ps范围达到最大值。随后驰豫阶段，由于缺陷复合作用导致缺陷数量逐渐减少，在10 ps左右达到平衡。OO缺陷数量则随着辐照时间增加而增加，并且在24.4 ps时仍未达到平衡，表明O原子恢复平衡是一个较为漫长的过程。在模拟结束时TiTi缺陷和OO缺陷数量比例极高，说明金红石在辐照条件下具有较强自我恢复能力。