小波熵理论在轨道列车走行部的故障诊断应用

赵肇信，李霆

（五邑大学，江门529020）

0 引言

轨道交通车辆是一个复杂的系统，拥有众多的子系统，其中列车走行部是最重要的子系统之一。它具有保证车辆灵活、安全平顺地沿钢轨运行以及可靠地承受作用于车辆各种力并传给钢轨，缓和车辆和钢轨的相互冲击等重要作用。但是，由于我国在针对轨道车辆故障诊断技术方面起步较晚，在早期轨道车辆的故障诊断主要是依赖有相关经验的技工人工检测，费时费力，容易产生失误。

随着我国经济与科研水平的上升，故障诊断技术在交通轨道列车的应用取得了较大进展。文献[1]提出通过Simpack 和ANSYS 软件构建列车齿轮有限元模型，引入EWT 对钢轨核伤信号进行分析，采用边际谱构建核伤特征取得良好的效果；文献[2]中提出采用DiCCA 分析法对列车轴承故障检测；文献[3]提出基于多域融合卷积神经网络的转向架故障诊断方法；文献[4]提出模糊理论与故障树分析相结合，建立了悬挂系统的模糊故障树，并对其故障概率进行了分析；文献[5]针对背景噪声对列车轮对故障信号的影响，采用FFT和谱估计对故障信号进行分析；文献[6]采用四种时域统计分析方法和共振解调作为频域分析方法，建立了列车轴箱轴承状态检测与故障诊断系统。文献[7]采用深度神经网络对转向架信号自适应地提取频谱中的故障信息，相比传统的智能诊断方法，深层神经网络具有更高的诊断精度。上述学者都对故障诊断技术在轨道交通车辆的应用做出了重要的贡献。但是，目前在轨道交通车辆作为特种车辆，转向架在实践检测中仍存在故障数据检测困难，精度相对较低和成本过高等问题[8]。

因此，本文通过多体动力学软件Simpack 构建列车模型，能够较容易大量获取不同通道列车正常运行，抗蛇形减震器故障以及一系悬挂弹簧失效时的三种工况的信号。在获取计算机仿真的三种工况信号的基础上，基于小波熵理论对三种工况信号进行分析并构建四种分类特征。最后通过支持向量机验证基于小波熵理论构建的四种划分特征进行分类的可靠性。

1 列车模型介绍

Simpack 是专家级机械系统动力学性能仿真分析软件，通过Simpack 的车辆—轨道动力学模块构建列车模型可以描述和预测列车运行过程中的动力学特性，通过内在解算器分析列车运行过程中各个部件的振动特性和预计运动位移、速度和加速度等物理量。因此，Simpack 成为轨道交通领域仿真中应该最为广泛的动力学分析软件之一。

为了能更真实的仿真车辆在轨道上的行驶状态，本文建立的列车模型涵盖了列车沿x,y,z 轴的转动分别为侧滚、点头和摇头，一共6 个自由度。同时，本文选取表1 和表2 的轨道车辆主要参数。

表1 车辆模型参数

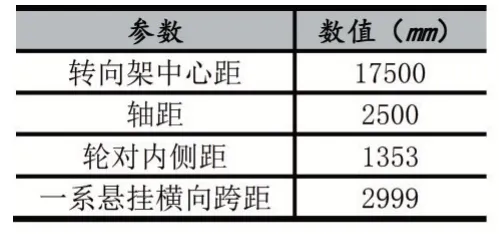
表2 车辆尺寸

建模思路及过程：

（1）建立列车轮对与轨道模型。选择Rail_Track模板，通过Create-Wheel Pair、Create Wheelset 以及Create Rail，根据所提供的参数建立车轮，轮对关系以及钢轨与轮对之间关系。为了仿真轮对与构架之间的相互作用关系，需要在轮对标记Marker 点作为定位。

（2）建立列车构架模型。构架的建立需要结合多个体（Body）互相组合，同时需要在构架上创建Marker点用于定位车轴定位部件上的轴承。

（3）建立转向架模型。将已建立的列车轮对与轨道模型导入到列车构架模型，通过Marker 点定义两者之间的一系悬挂关系。

（4）建立整车模型。选取Car Model，输入相关参数，同时修改车体铰接类型与创建Marker 点。导入转向架模型，通过Marker 点定义两者之间的二系悬挂关系。建立抗侧滚杆，抗蛇形减震器以及牵引杆等部件在整车的力学关系。

（5）通过预载荷（Preload）使列车达到静平衡状态。

列车模型建立完成后，需要检查各个部件之间的关系是否完整和合理。通过二维拓扑图可以清晰全面的反应各个部件之间的连接关系，如图1 为转向架二维拓扑图，图2 为整车二维拓扑图，图3 为列车模型三维视图。

图1 整车二维拓扑图

图2 列车模型三维视图

2 信号小波熵特征

小波变换是学者Jean Morlet 在傅里叶变换的基础上提出的，从多个尺度对信号时频域展开分析。信息熵是学者C.E.Shannon 基于概率统计原理进行第一次定义，通过熵的角度反映信号的混乱程度，相关性等指标。由于列车在运行过程受速度、环境以及钢轨激扰等因素的影响，列车在不同的运行工况时，由传感器检测的振动信号是包含大量复杂频率成分的非平稳随机信号。因而，在本文结合小波变换和信息熵在处理无规则非线性复杂信号的优点。对列车的振动信号通过小波变换进行多尺度分解，基于信息熵理论提取不同尺度范围内反映信号复杂度及混乱程度的小波熵特征。针对列车正常运行，抗蛇形减震器故障以及一系悬挂弹簧失效时的三种工况的信号，本文选取四种小波熵特征对列车三种工况信号进行特征提取与分析。

2.1 小波变换

快速正交小波变换是基于多分辨分析，通过正交小波基将信号在不同尺度下进行分解。其实现过程相当于通过一组高、低通滤波器将原始信号进行分解，将逼近信号再一次通过高、低通滤波器获得下一层逼近信息和细节信息，逐层分解[9]。设非平稳信号f(x)，通过快速正交小波变换分解为m 层，第j 层分解尺度在时刻高频分量系数dj(k)，低频分量系数aj(k)，通过单支重构后获得信号分量Dj(k)和Aj(k)，则原始信号序列可以通过各分量之和进行表达：

为了统一，将Am(k)用Dj+1(k)代替：

为了与下文描述统一，本文使用Dj+1（k）表示小波变换后高频分量系数和低频分量系数所组成的向量矩阵，式中j=1,2,…m，m 为正整数,k=1,2,…,L 为第k 个采样点。

2.2 四种小波熵的定义

在本文采取Tsallis 小波能量熵，小波奇异熵，小波近似熵以及小波时间熵。 引入滑动时间窗W（Qs(δ),ω,δ），Qs=1+Sδ，S 为相对起始信号步长，ω∈N为窗宽因子，δ ∈N 为滑动步长。设E=E1,E2……Em为信号f(x)在m 个尺度下的小波能谱。根据正交小波变换特性可知，在某一时间窗内的信号总能量为m 个尺度的信号能量之和，从而定义小波能谱熵（WEE）：

（1）Tsallis 小波熵（Tsallis Wavelet Energy Entropy，TWEE）

Tsallis 小波熵是基于Shannon 小波熵的改进，通过非广延参数进行调节，避免小波变换过程因频率分配不均而造成能量缺失造成误差。信号f(x)进行m 层小波变换后，各个尺度上的的小波能量谱E=E1,E2,…,Em，从而定义Tsallis 小波熵的计算式为：

式中：q 为非广延参数，q∈R

（2）小波近似熵（Wavelet Approximate Entropy，WAE）

原始信号f(x)经过小波变换，第j 尺度下变换系数为Dj(k)=(dj(1),dj(2),…,dj(k)) 。计算S=Dj(k)=(dj(1),dj(2),…,dj(k))的小波近似熵，过程如下：

①确定维数p，通过信号S 构造p 维向量

②计算构造向量X(i)中任意两向量间的距离d(X(i),X(l))和关联程度Ci(p,r)：

式中：h(·)为Heaciside 函数；r 为相似容限。

③计算平均自相关程度Φ，求解小波近似熵

（3）小波奇异熵（Wavelet Singular Entropy，WAE）

原始信号f(x)进行m 层小波变换后获得变换系数矩阵Dm×l。根据奇异值分解理论，对与矩阵Dm×l，必然存在Dm×l=Um×sΛs×sVm×l其中对角矩阵Λs×s的主对角线元素λi非零，且λ1>λ2……λs，因此定义小波奇异熵的计算式为：

（4）小波时间熵（Wavelet Time Entropy，WTE）

原始信号f(x)经过小波变换，第j 尺度下变换系数为Dj(k)=(dj(1),dj(2),…,dj(k))，在此变换系数定义上通过划分为L 个互不相交的区间。设pm(Zl)为小波系数dj(k)∈W（Qs(δ),ω,δ落 在 区 间Zl的 数 目 和 落 在W（Qs(δ),ω,δ上的总数目比值，因此在j 尺度下的小波时间熵可以由此定义：

以上四种小波熵在不同层面的不同角度定义和描述被分析信号在小波变换后变换系数在系统整体或者局部中信息的复杂和混乱程度。

3 仿真实验

3.1 实验方法

在本文，数据来源于多体动力学软件Simpack 构建的列车模型。为保证列车三种运行工况的真实性，列车模型的车轮踏面外形采用LMA 踏面，钢轨采用CN60 钢轨，轮对内侧局沿用中国标准1353mm，充分考虑轮轨接触几何非线性、轮轨螺滑非线性和非线性悬挂，该车辆模型由1 个车体、2 个构架、4 个垂向减震器，2 个防侧倾杆，4 个抗蛇行减振器等组成，仿真使用武汉-广州轨道激励谱。

在列车模型转向架关键部位设置传感器，包括构架、车体、抗蛇形减震器以及车轴。通过计算机分别仿真列车正常运行，抗蛇形减震器故障以及二系悬挂弹簧失效时的三种工况的加速度横向、纵向和垂向和位移纵向信号。每一种工况对应34 个通道信号，对应不同位置和不同方向的振动物理量

采集列车在120km/h 的运行状态下，采样频率为256Hz，仿真时间60s。通过传感器采集列车正常运行，抗蛇形减震器故障以及一系悬挂弹簧失效时的三种工况在34 个通道中的工况信号，其中列车前转向架中部纵向加速度通道的三种工况的加速度信号和幅值谱图分别为图3 所示。

图3 三种工况的信号和幅值谱

3.2 特征提取

数据选取列车在120km/h 运行情况下，采样频率为256Hz，采样时间为5s，列车前转向架中部纵向加速度通道的三种工况信号。对三种工况信号进行小波变换，目前对于基小波的选择仍没有明确的指导方法。根据列车在运行过程中，由于外界环境或轨道激励等因素所产生的列车非平稳信号具有突变型，奇异性等特性，所以选取具有较高时频分辨率的正交小波db4作为基小波。初步，根据三种工况信号的采样频率和特征频率确定小波分解层数为3 层，滑动窗宽度为200，滑动步长为1。三种工况信号单支重构系数和4种小波熵特征如图4 和图5。

图4 三种列车运行工况单支重构信号

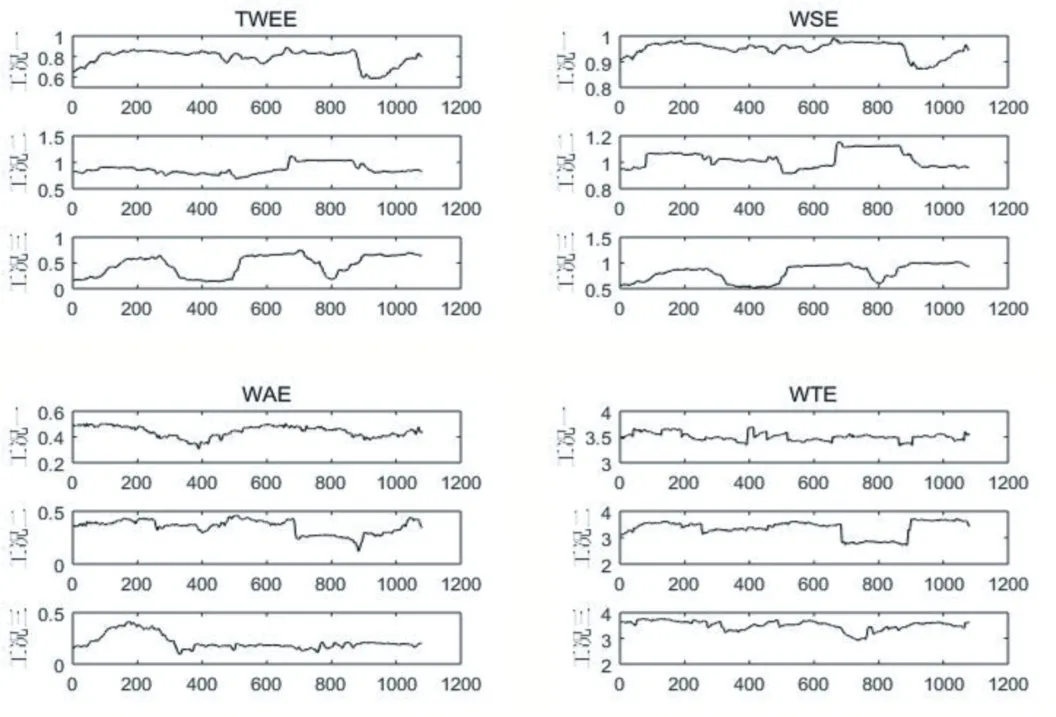
图5 三种列车运行工况小波熵特征

从图5 可以看出，仅从一个小波熵特征来看，每一种工况下小波熵特征的变化范围是有区别的，这说明了不同小波特征描述下三种工况信号的复杂度是不同的。对于列车运行时的工况振动信号，Tsallis 小波熵通过对非广延参数q 调整，避免小波变换中因频率分配不均而造成能量流失而导致误差，从而更准确地揭示振动信号时域和频域之间的能量关系。列车正常运行和抗蛇形减震器失效的两种工况TWEE 值都处于0.7-1.5 之间，而一系弹簧失效时TWEE 值处于0-0.6之间，因而可以说明一系弹簧发生故障。小波近似熵则是对被分析信号小波变换某一层小波系数不规则程度的量化。小波奇异熵能反应在时域和频域空间上被检测信号的模式。小波时间熵对被检测信号的成分和参数具有很强的检测能力。

如果单单从一种小波熵特征来看并不能很好地区分三种列车运行工况，但是小波熵特征之间的具有互补性。因此，在本次仿真实验中，结合小波变换和信息熵理论，从不同角度对小波变换系数的信息能量分布进行定义，选取四种小波熵作为特征。

3.3 基于SVM分类结果

支持向量机（SVM）具有解决线性或非线性信号情况下分类能力。在线性情况下，通过构造一个最优的分类面进行分类。在非线性情况下，通过将核函数低维空间的样本映射到高维特征空间中，同时计算在高维空间中的最优分类超平面。

在本文通过Matlab 中的LibSVM 工具包选择多项式核函数对三种工况进行分类识别，先初步决定核函数的阶数为3，采用交叉验证法选取参数C 和g（其中C 为惩罚因子，g 为核函数的半径），通过模型计算三种工况分类准确率。选取不同大小不同的参数对分类准确率的影响如表3。

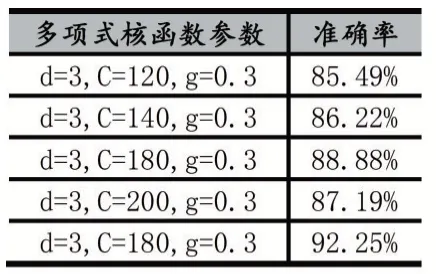
表3 核函数不同参数下的识别率

从表2 可以看出，三种工况的分类能达到较高的准确率，且具有一定的鲁棒性。其中惩戒因子C 是指误差的宽容程度，惩戒因子的过高或者过低会造成欠拟合或者泛化能力差等问题。Gamma 的大小则决定了支持向量的数量。因此当本文选择参数d=3,C=180,g=0.3 时，三种工况分类的准确率能达到92.25%。

4 结语

在本文，采用多体动力学软件SIMPACK 构建列车模型，通过计算机仿真获得列车正常运行，抗蛇形减震器故障以及一系悬挂弹簧失效时的三种工况的信号可以为实践故障检测提供理论上的探索同时也解决列车走行部故障数据缺乏等问题。然后，基于小波变换和信息熵相结合的小波熵理论将三种工况信号作为研究对象，提取每种工况的四种小波熵特征，从而为列车转向架故障诊断应用中选取分类特征提出一种新的思路和方法。最后，通过交叉检验选取恰当的多项式参数，通过支持向量机使得三种工况的识别率达到92.25%，证明小波熵理论在列车转向架故障诊断中的可行性以及可靠性。