因子分析模型L与应用的研究进展
石 立,赵慧琴,林海明
(广东财经大学 华商学院,广东 广州 511300)
0 因子分析模型L的提出
Spearman[1]在对学生智力的统计分析中,提出了因子分析。2004年,在纪念因子分析发表100周年之际,Cudeck等[2]认为,因子分析是社会科学统计方面有重大影响的成功事件之一,是多元统计中价值无可估量的统计工具之一,是行为研究方法论的支柱之一,因子分析的应用充满活力,前景广阔。迄今国内外的文献:英国统计学家肯德尔[3]、著名统计学家张尧庭和方开泰[4]、美国统计学家Johnson和Wichern[5]、德国和比利时统计学家Härdle和Simar[6]、国际著名统计学家Fan等[7]、Yacine等[8]、Kei等[9],使用了如下传统模型:
因子分析模型设p维可观测随机向量x=(x1,…,xp)′,E(x)=μ,Cov(x)=∑,记公因子随机向量f=(f1,…,fm)′和特殊因子随机向量ε=(ε1,…,εp)′,要求:
x-μ=Lf+ε,
其中,L=(lij)p×m称为因子载荷阵,lij称为变量xi在公因子fj上的载荷,求L、f,使:
E(f)=0,Cov(f)=Im,E(ε)=0,Cov(ε,f)=0,
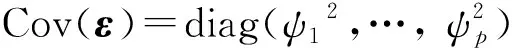
称此为正交因子分析模型(注:该模型无优化条件,下称旧模型)。
旧模型的估计方法,公因子载荷阵L有:主成分法、主因子法、最大似然法等[5];公因子f有:1939年Thomson的回归法、1948年Bartlett的加权最小二乘法等[3]。
著名统计学家方开泰[10]认为,因子分析是多元分析降维的一种方法,因子有较鲜明的解释,即因子分析的目的是降维并合理解释变量。但旧模型和理论还是很不完善,从数学上看,还存在许多问题[4]。国内外著名统计学家总结如下4个基本问题:
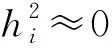
问题2 降维的方法还有主成分分析,在因子与主成分方面,白雪梅[11]认为,对主成分象因子分析那样实施方差最大化正交旋转,结果不是主成分,故对主成分再实施旋转是错误的。阎慈琳[12]认为,用主成分分析不合适时,用因子分析中方差最大的正交旋转可能取得较好的效果,并给出了应用实例。G S·马达拉等[13]认为,因子和主成分的理论关系与实际差异,是令人非常感兴趣的问题,但他没有解决此问题。
问题3f的解方面,M·肯德尔[3]认为,m 问题4 优良性方面,美国科学院院士、著名统计学家Anderson[14]讨论了f估计的优良性问题,并提出了无偏性、平均预报误差准则。但Johnson和Wichern[5]认为,因子分析优良性准则尚未很好量化,即优良性的量化是人们一直需要解决的问题。 据查,迄今对上述4个基本问题的关注较少,如Fan等[7]、Yacine等[8]、Kei等[9]。 x-μ=L*f*+ε*, (1) E(f*)=0,Cov(f*)=Im,E(ε)=0,Cov(ε,f*)=0 (2) tr(L*′L*)达到最大。 (3) tr是方阵的迹,tr(L*′L*)是因子f*解释变量的方差贡献。下称此模型为新模型或模型L。 新模型特点:式(3)是新旧模型的不同之处,它改变了旧模型无优化条件的状况;新模型有可行解,改变了旧模型只有估计的历史。这些成为解决上述4个基本问题的支点。 林海明[15]用张尧庭给出的标准化主成分法,求出了新模型的可行解:主成分法的因子载荷阵L*及其回归的因子得分f*。以下介绍此方法。 主成分分析模型的解:设主成分Z=(z1,z2,…,zp)′,E(Z)=0,则 Z=U′(X-μ) (4) 这里U=(u1,u2,…,up)=(uij)p×p,UU′=Ip,∑ui=λiui,Var(zi)=λi(i=1,…,p),λ1≥…≥λm≥…≥λp≥0。 标准化主成分法:式(4)左乘U,有: X-μ=UZ=(u1,…,um)(z1,…,zm)′+(um+1,…,up)(zm+1,…,zp)′ (4)′ X-μ=L0f0+ε0 经比较和验证,这里的L0是因子分析主成分法估计的初始因子载荷阵,f0是用初始因子载荷阵L0回归的初始因子(得分)[16]。 引理1(Weyl)[20]设∑和B都是n阶实对称阵,∑的特征值是λ1,…,λp,λ1≥…≥λp,B的特征值是v1,…,vp,v1≥…≥vp,若∑-B是非负定的,则λi≥vi(i=1,…,p)。 问题1解答:林海明[21]用新模型的可行解、德国数学家Weyl的引理1,求出新模型f*的解是:主成分法因子载荷阵L*回归的因子得分f*,f*能降维、能较鲜明地解释变量且不会遗漏变量解释,即更好的因子分析模型是因子分析模型L,解决了问题1。 问题2解答:郭显光[22]从SPSS软件计算的角度,给出了初始因子载荷阵列向量与主成分系数向量的关系,但没有给出因子与主成分的关系与计量上的差异。林海明等[23]应用因子分析新模型及其解、主成分分析模型及其解,找到了因子与主成分的理论关系,设因子分析模型L的未旋转因子解为初始因子,旋转后因子解为旋转后因子,则有初始因子等于标准化主成分;实际差异为方差和旋转。因此,方差大于1的主成分取值范围,较方差全为1的因子的取值范围大,故二者计量不同,不可混淆,这解决了G S·马达拉[13]没有解决的问题2。据中国知网查阅,文[23]的结果被较多领域的研究论文引用,产生了较高的学术影响。 问题3解答:林海明等[24]在旧模型中,将非零特殊因子标准化并化简旧模型,应用新模型及其可行解,求出了旧模型公因子f的解,由此得出:公因子f含有方差贡献大的公因子和多项互不相关的误差项,不含互不相关的原始变量,这明确地证实了Johnson和Wichern、张尧庭和方开泰的观点:公因子f不能降维且会遗漏变量解释。突破了M·肯德尔认为不可能求出因子分析模型解的问题3,说明了因子分析模型L是更好的。 问题4解答:林海明[25]在方开泰教授的指导和帮助下,用因子分析目的量化条件,建立了降维性、解释性和拟合性的优良性量化准则,证明了因子分析新模型具有这些优良性,说明了无偏性在因子分析中作用不大,主因子法、最大似然法不能达到这些优良性。解决了Johnson和Wichern[5]认为不幸的问题4。 自此,林海明等在方开泰教授、陈家鼎教授等的指导和帮助下,建立了因子分析改进的模型:因子分析模型L,其改进之处在于:解决了上述4个基本问题。上述4个问题的解决,得到了国内较多研究者的引用,如朱建平等[26]将因子分析模型L及其应用,写入教育部高等学校统计学类专业教学指导委员会推荐用书、博雅·21世纪统计学规划教材《应用多元统计分析》。为了应用因子分析模型L的结果,赵慧琴[27]给出了如何用SPSS软件计算因子分析模型L的应用结果。 3.1 主成分分析综合评价的条件方面,主成分能解释变量是主成分分析综合评价推断与评价的前提,刘树梅等[28]认为,主成分的具体涵义是什么,许多文献没有给予较为清楚的解释,从而影响到结果的可信度。王学民[29]认为,对主成分建立综合评价函数的方法是错误的。林海明等[30]在正向变量标准化下,应用因子分析新模型的解释性及其初始因子载荷阵是变量与主成分的相关阵的关系,得出了主成分有具体涵义的条件(此称为初始因子载荷阵较靠近简单结构)。设p列初始因子载荷阵每行元素最大绝对值的平均数为b0,因子分析新模型的不同列旋转后因子载荷阵每行元素最大绝对值的平均数最大者为bΓ,如果b0≥bΓ或b0≈bΓ,则主成分有具体涵义(如果此条件不满足,则需要改用其它方法进行综合评价,如旋转后因子分析)。解决了主成分能解释(命名)的条件问题,并证明了主成分分析综合评价函数y=α1F1+…+αmFm(αi=λi/p,λi是主成分Fi的方差)达到合理性条件为:①x= (x1,…,xp)′是正向、标准化的,②初始因子载荷阵较靠近简单结构,③主成分F=(F1,…,Fm)′正向,④主成分F中的每个Fi与变量x中的一些变量显著相关。据中国知网查阅,该论文结果被较多领域的论文引用,产生较大的学术影响。 3.2 对应分析方面,对应分析法的目的是将样品与变量降维表示在低维图中,从中得出变量之间、样品之间、变量与样品之间的关系。对应分析早在1933年由Richardson和Kuder[31]提出。从20世纪30年代到20世纪70年代,许多著名的统计学家如Fisher[32],Maung[33],Guttman[34],Williams[35],Lancaster[36],Hayashi[37]以及文献[38-43]等参与研究对应分析模型和计算准则,各自声称建立了一种新的统计方法,并冠以不同的名字,但这些方法的优化准则基本等价,计算结果基本一致,这在学科发展史上是较罕见的[44]。迄今国内外流行的传统对应分析法是Benzécri[45](下称B氏方法)在1970年提出的,它是对等性变换+R型因子分析+Q型因子分析的降维图。但国内外有专家质疑,对等性变换是非线性变换,其改变了数据的特征,能达到对应分析的目的吗?如杜子芳[46]认为:当变量量纲不同时,对等性变换对数据阵中同一样品的变量值相加的结果不可解释(如某教室10张凳子+10张桌子=20的结果不可解释),即B氏方法的对等性变换一开始就存在不可解释的问题。在文中指出,二因素独立时,对等性变换会把数据阵变为零矩阵,说明对等性变换对数据阵的改变非常大,甚至不能解决问题。刘照德和林海明[47]在方开泰教授的指导和帮助下,根据对应分析目的,建立对应分析改进模型,在变量标准化下,以因子分析新模型的因子f*建立坐标系,用因子载荷阵L*表示变量、因子f*的样品值表示样品的图。此图称为因子双重信息图。并证明了在变量标准化下,用主成分法的因子载荷阵L*及其回归的因子f*作出的因子双重信息图是对应分析改进模型的解,能优良地达到对应分析目的,是更好的方法,并给出了实证。 3.3 因子分析综合评价的条件方面。邱东[48]认为,因子分析综合评价要完成去量纲、去相关、定权数、降维这4项基本工作,在变量有一定相关时应用比较理想。但王学民[29]认为,对因子得分建立综合评价函数的方法是错误的。而大量的综合评价研究都用因子得分建立综合评价函数。故有问题:因子分析综合评价还需要哪些合理性条件?林海明等[49]在正向变量标准化下,应用因子分析新模型的解释性、降维性及其因子载荷阵是变量与因子的相关阵的关系,得出了因子有具体涵义的条件(此称为因子载荷阵L较靠近简单结构):设p列初始因子载荷阵每行元素最大绝对值的平均数为b0,因子分析新模型的不同列旋转后因子载荷阵每行元素最大绝对值的平均数最大者为bΓ,1)如果b0≥bΓ或b0≈bΓ,则初始因子有具体涵义,此时用初始因子作综合评价较合理;2)如果b0 4.1 聚类分析拓展研究。任雪松[51]认为,p个变量不相关、且有相同的方差时,使用欧式距离聚类才合适,效果也较好,否则有可能导致错误结论。我们认为,聚类分析的结果,不能解释同类样品优劣性的原因,不能提出更好决策的建议。故有问题:用新模型的因子样品值作聚类分析,聚类分析效果何时更好? 4.2 判别分析拓展研究。判别分析有着许多重要的应用,如吴世农[52]的文献等。我们认为,判别分析的结果,不能解释新样品所在类别优劣性的原因,不能对新样品优劣性提出更好决策的建议。故有问题:用新模型的因子样品值作判别分析,判别分析效果何时更好? 4.3 结构方程模型拓展研究。现行的结构方程模型中,测量方程参数的识别没有优化条件(侯杰泰等[53]),众所周知,这不易得到优良估计,甚至误差较大,以致不能解决问题。故有问题:用新模型作为结构方程模型的测量方程,结构方程模型效果更好吗? 4.4 回归分析拓展研究。多元回归分析时常出现多重共线性,模型需要修正(庞皓等[54])。将p个自变量用新模型的少数几个因子替代,建立一个因变量与少数几个因子的回归模型,即因子回归分析。故有问题:因子回归分析效果何时更好? 传统因子分析模型公因子存在不能降维、会遗漏变量解释等缺陷,优良性准则没有更好的量化。因子分析模型L解决了这些量化问题,具有能降维、能较清晰解释数据、误差较小的优良性;解决了因子与主成分的理论关系与实际差异问题;拓展至主成分分析综合评价中,找到了主成分能命名的条件等,拓展至对应分析中,解决了传统对应分析较大改变数据的缺陷,较清晰地解释了多元数据;其拓展至因子分析综合评价中,解决了因子分析综合评价合理条件的问题。聚类分析、判别分析、回归分析、结构方程模型等都是较重要的多元分析方法,都需要较清晰的解释多元数据,以便更好地解决问题。故将因子分析模型L的教学与应用普及化,并拓展研究至这些方法中,将产生更大的学术价值和应用价值。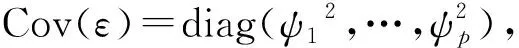


1 标准化主成分法与Weyl的一个引理
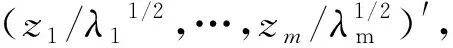
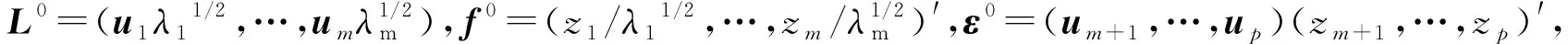

2 4个基本问题解答综述
3 因子分析新模型的拓展研究
4 因子分析新模型待拓展的研究
5 结论与建议

