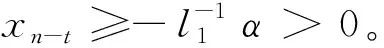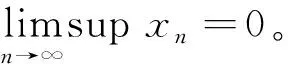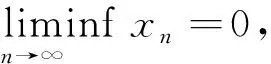二阶中立型时滞差分方程解的振动性准则
张思逸
(湖南幼儿师范高等专科学校,湖南 常德 415000)
0 引言
二阶中立型差分方程的振动性理论在近十几年来得到了广泛的关注,主要体现在此类方程与某些类似微分方程的现象非常接近。此外,在物理学和其他领域有着许多应用(见文献[1,5]),特别是带有中立型与时滞项的差分方程。 近些年来,二阶中立型差分方程关于解的振动性问题的研究受到很多关注,见文[2-4,6,9-10]。但是,二阶中立型时滞差分方程的振动性研究相对较少。文献[7]中研究了如下的一类变系数的二阶中立型时滞差分方程
Δ2[x(n)+p(n)x(n-m)]+Q(n)H(x(n-t))=0n≥n0
的振动性。在此基础上,文献[8]通过分析技巧也讨论了如下的一类变系数的中立型时滞差分方程
Δ[anΔ(xn+pnxn-k)]+gnH(xn-t)=0n≥n0
(1)
的振动性。其中an>0,pn,gn∈R,k,t,n0∈Z+且Δ是向前差分算子,即Δxn=xn+1-xn,Δ2xn=Δ(Δxn)。
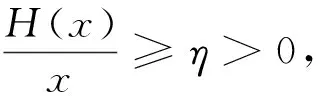
1 预备知识及主要定理
定义1 如果存在正整数N,对任意的n≥N,若方程(1)都有解xn≥0,那么称{xn}是方程的最终正解,反之称为最终负解。
定义2如果方程(1)的解{xn}既不是最终正解也不是最终负解,则称之为振动的,否则称之为非振动的。
定义3如果方程(1)的所有解都是振动的,则称方程(1)是振动的,否则称之为非振动的。
为了得到二阶中立型差分方程振动解和其渐进性质,我们需要引入如下的假设条件:
(H1) 存在λ≥0,对于几乎所有的u,v≥0,使得H(u)+H(v)≥λH(u+v)成立;
(H2)H(uv)=H(u)H(v),其中u,v∈R;
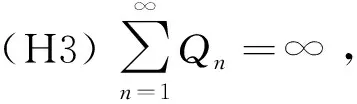
定理1若0≤pn≤p<∞, 如果条件(H1)-(H3)以及
(2)
成立,则方程(1)是振动的。
证明假设xn是方程(1)的一个非振动解,那么存在n0∈N+,使得当n≥n0时,有xn>0或者有xn<0。
(i)不妨设对任意的n≥n0+k,都有xn>0且xn-k>0,令
yn=xn+pnxn-kn≥n0+k,
则从方程(1)可知
Δ[anΔyn]=-gnH(xn-t)<0n≥n0+k
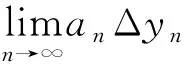
假设对任意的n≥n0+k有anΔyn<0,由(2)式可以知道,当n≥n0+k时有an>0。那么存在n1≥n0+k与实数c<0,使得当n≥n1时有
(3)
对上式(3)两边同时从n1到n-1求和,则有
即由(2)可得,当n→∞时,

对方程(1)的n取为n-k>0,两边同时乘上H(p),得到
H(p)Δ[an-kΔyn-k]+H(p)gn-kH(xn-k-t)=0,
(4)
对上式(4)加上(1),可以得到
Δ(anΔyn)+gnH(xn-t)+H(p)Δ[an-kΔyn-k]+H(p)gn-kH(xn-k-t)=0,
使用(H1)-(H3),当n≥n0+k+t时,即有
0=Δ(anΔyn)+gnH(xn-t)+
H(p)Δ[an-kΔyn-k]+H(p)gn-kH(xn-k-t)
≥Δ(anΔyn)+H(p)Δ[an-kΔyn-k]+
Qn[H(xn-t)+H(p)H(xn-k-t)]
≥Δ(anΔyn)+H(p)Δ[an-kΔyn-k]+λQnH(yn-t)
≥Δ(anΔyn)+H(p)Δ[an-kΔyn-k]+λQnH(a)。
(5)
对上式(5),两边从n1=n0+t到n-1求和,则有
则当n→∞时,上式与(H3)矛盾。
(ii) 设当n≥n0都有xn<0, 则当n≥n0时,令yn=-xn。由差分算子的线性性质与假设(H2),则有
Δ[anΔ(yn+pnyn-k)]+gnH(yn-t)=0,
于是利用相似的方法,就可以得到结论,证毕。
定理2若0≤pn≤p<∞,如果条件(H1)-(H3)以及
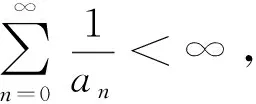
成立,则方程(1)是振动的。
该庭院位于小区整体建筑最东侧,西靠另一单元建筑,南为大门入口,北侧东侧有围墙,后院面积约为147.3 m2.侧院为狭长通道,宽约4.65 m,长约8.7 m.前院面积较小,长约7 m,宽约4.5 m(图1).从前院经侧院两段连续下沉台阶至后院.该小区庭院共3个部分:前院、侧院和后院(图2).由于占地面积及建筑形式的限制,规划占地为不规则几何形,从规划面积上看,属于小尺度空间景观设计范畴(图3).
证明假设xn是方程(1)的一个非振动解,那么存在n0∈N+,使得当n≥n0时,有xn>0或者有xn<0。 不妨设对任意的n≥n0+t,都有xn>0且xn-t>0。
当xn<0时,类似地可以证明。令
yn=xn+pnxn-kn≥n0+k,
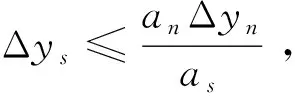
0=Δ(anΔyn)+gnH(xn-t)+
H(p)Δ[an-kΔyn-k]+H(p)gn-kH(xn-k-t)
≥Δ(anΔyn)+H(p)Δ[an-kΔyn-k]+
(6)
对(6)从n2=n0+k+t到n-1求和,就有
也就是
≤-[anΔyn-an2Δyn2+H(p)(an-kΔyn-k-an0+kΔyn0+k)]
≤-[anΔyn+H(p)(an-kΔyn-k)]
≤-(1+H(p))anΔyn。
于是就推出
与
-(yn-yn2)≤yn2,
这说明{yn}是单调有界的序列,并且
这与假设矛盾,故方程(1)是振动的,证毕。
定理3若-1≤pn≤0, 如果条件(2),(H2)以及
(7)
成立, 则方程(1)是振动的。
证明令xn在[0,∞)上是(1)的无界解。由上述定理的证明可知anΔyn在[n1,∞)上是最终非增的,其中n1=n0+k。
因为yn是单调的,所以存在着n2>n1,n2=n0+k+t,使得对任意的n≥n2都有yn>0或者yn<0。
现在假设yn<0对任意的n≥n2都成立,则由已知条件与(3)可以得到xn xn 上式与xn无界矛盾,故对任意的n≥n2一定有yn>0。 下面假设anΔyn>0,n≥n2。于是可知yn≤xn,这样就得到了 Δ(anΔyn)+gnH(yn-t)≤0。 由集合{yn}的最终非减可以知道,存在常数c>0,使得对所有n≥n2都有yn≤c,即 Δ(anΔyn)+H(c)gn≤0,n≥n2 上式从n2到n-1求和,即得 所以就推出了 这显然与(7)矛盾, 所以anΔyn<0。 后面证明可类似定理1,证毕。 定理4若对l1,l2>0有-∞<-l1≤pn≤-l2<-1,如果再有条件(2),(H2)和(7)成立,则方程(1)的每个有界解要么是振动的,要么当n→∞时收敛于0。 证明假设xn是方程(1)在[n0,∞)上的一个解。 根据定理1 中相似的证明方法就可得到在[n1,∞)上anΔyn与yn是同号的,其中n1=n0+k。因此,根据定理1,(2)和{yn}的有界性,当xn>0时,我们只需讨论: 当β∈(-∞,0)时有limn→∞yn=β。 类似地可以证明xn<0的情况。 假设β∈(-∞,0),则存在α<0,使得对任意的n≥n2,n2=n0+k+t,都有yn-k-t<α。故 -l1xn-k≤yn-xn≤yn。 即 -anΔyn-an3Δyn3<∞, 上式与(7)矛盾,所以β=0。于是