SDN中基于流重定向的MPLS标签算法
王莅晟,伊 鹏,谷允捷,江逸茗
(中国人民解放军战略支援部队信息工程大学 信息技术研究所,郑州 450002)
0 概述
软件定义网络(Software-Defined Network,SDN)作为未来最有可能取代传统网络的新型网络体系结构之一,在近几年得到了广泛的应用研究[1-3]。软件定义网络采用了数控分离的机制,相对于传统网络架构,拥有控制逻辑集中、开放可编程、细粒度流管控的优势。
软件定义网络的控制平面通过OpenFlow[4]协议掌握数据平面的全局拓扑,当系统中到达一条新流时,交换机首先会在已存储的流表项中查找是否有匹配条目,如果存在与该流匹配的流表项,则根据流表项对新流进行转发。如果没有匹配条目,则数据平面的交换机将元数据与新流前128 MB的内容封装成Packet-In消息通过OpenFlow代理(OpenFlow Agent,OFA)向上传递给控制平面,控制平面对路由进行计算后通过下放流表的方式在沿途交换机上安装相应转发规则,新流根据流表中的转发规则进行转发,下放的流表均安装在三态内容寻址存储器(Ternary Content Addressable Memory,TCAM)[5]中。
在软件定义网络中,TCAM模块负责流表项的更新、存储和查找工作,然而由于TCAM并非专为OpenFlow交换机设计,其具有成本高、功耗大、容量小、流表更新操作速率较慢等缺陷,导致数据包下行链路存在性能瓶颈问题,基于Pica8交换机[6]测出的TCAM流表安装速率仅为每秒200条,相比早期控制平面,单个NOX[7]控制器达到了每秒30 000条处理速度,在使用并行的Maestro控制器[8]下甚至达到每秒600 000条的请求处理速度,每秒200条的流安装速率很容易出现流表安装速率跟不上控制器处理速率,进而出现下行控制链路拥塞以及流请求无法得到及时传输,严重影响通信质量的情况。
研究人员对TCAM的研究大多集中在流表存储容量[9-12]。文献[9]介绍了一种表项聚合的方式,通过将多个表项通过特征合并为一个表项,节省流表项空间,表项聚合分为非前缀聚合和前缀聚合,然而SDN中许多多元匹配字段不适合聚合,因此表项聚合并不适用于大多数情况。文献[10]介绍了一种针对timeout的表项优化方式,通过动态改变表项存活时间来降低表项容量浪费的情况,但是这种方式可能会增加下行控制链路的压力,造成某些流表多次下发。
现有的研究多数忽略了交换机下行控制链路可能出现的拥塞问题,这可能导致当短时间内控制器向交换机下发大量流表时,交换机TCAM中仍然存在存储空间,但是由于流表更新速率过慢导致无法快速安装流表,进而导致下行控制链路拥塞,引起TCAM资源的浪费以及用户服务延时的增加。文献[13-14]指出现有网络硬件条件下软件定义网络控制链路存在性能瓶颈。文献[8]提出将流请求重定向到虚拟交换机,利用虚拟交换机较强的CPU处理能力进行packet-in消息上传和流表项安装,然而虚拟交换机具有较高的部署成本,不适用于大规模网络部署。文献[15]针对该问题提出了一种改进的基于随机Runting的路由部署(Random Ruting Dployment,RRD)算法,通过添加约束的方法从所有可能路由路径中选出最优路径,然而该问题是一个NP难问题,只能得到近似解,且计算过程较为复杂。
本文结合文献[16]提出的数据包封装多协议标签交换(Multi-Protocol Label Switching,MPLS)与分段路由(Segment Routing,SR)的方法,提出一种基于流重定向的MPLS标签算法FRML。通过设置触发阈值,当路径中需安装的流表数超过阈值时,选取路径上合适的交换机,仅向该交换机下发添加标签的流表,之后的交换机只需根据打好的标签即可选择相应端口的转发操作,以缓解交换机中下行控制链路资源紧张的状况。
1 问题分析与建模
1.1 问题分析
从OpenFlow交换机工作原理可以发现,SDN网络数据包传输依赖于OpenFlow交换机与SDN控制器之间的信息交互,然而由于TCAM性能限制,流表项更新速率仅为每秒200条,这就导致当系统内突发流量过大或遇到恶意攻击时很可能会出现TCAM存储空间仍然充足,但是流表无法及时更新到TCAM中的情况,使得SDN网络下行控制链路拥塞,进而导致新流无法得到及时传输,严重影响系统性能。
对于下行控制链路拥塞问题,将形成拥塞的流表项分为两类:一类是下发到源节点的流表项,数据最初存储于源节点的缓存中,因此无论是传统方法还是本文采用的MPLS算法都需要在源节点下发流表,此类流表的负载始终存在,只能通过重定向等方法利用其他交换机分担;另一类是控制器计算出流路径后在路径上的交换机中下发的流表项,此类流表项可以使用MPLS算法用数据前缀的方式代替,因此属于不是必须的下行控制链路负载,但是需要占用数据链路带宽,在数据链路负载和线性控制链路负载之间做出权衡,选择路径中部分交换机下发流表进行数据流的转发操作。
1.2 问题建模
1.2.1 系统元素
系统元素主要包括以下3种:
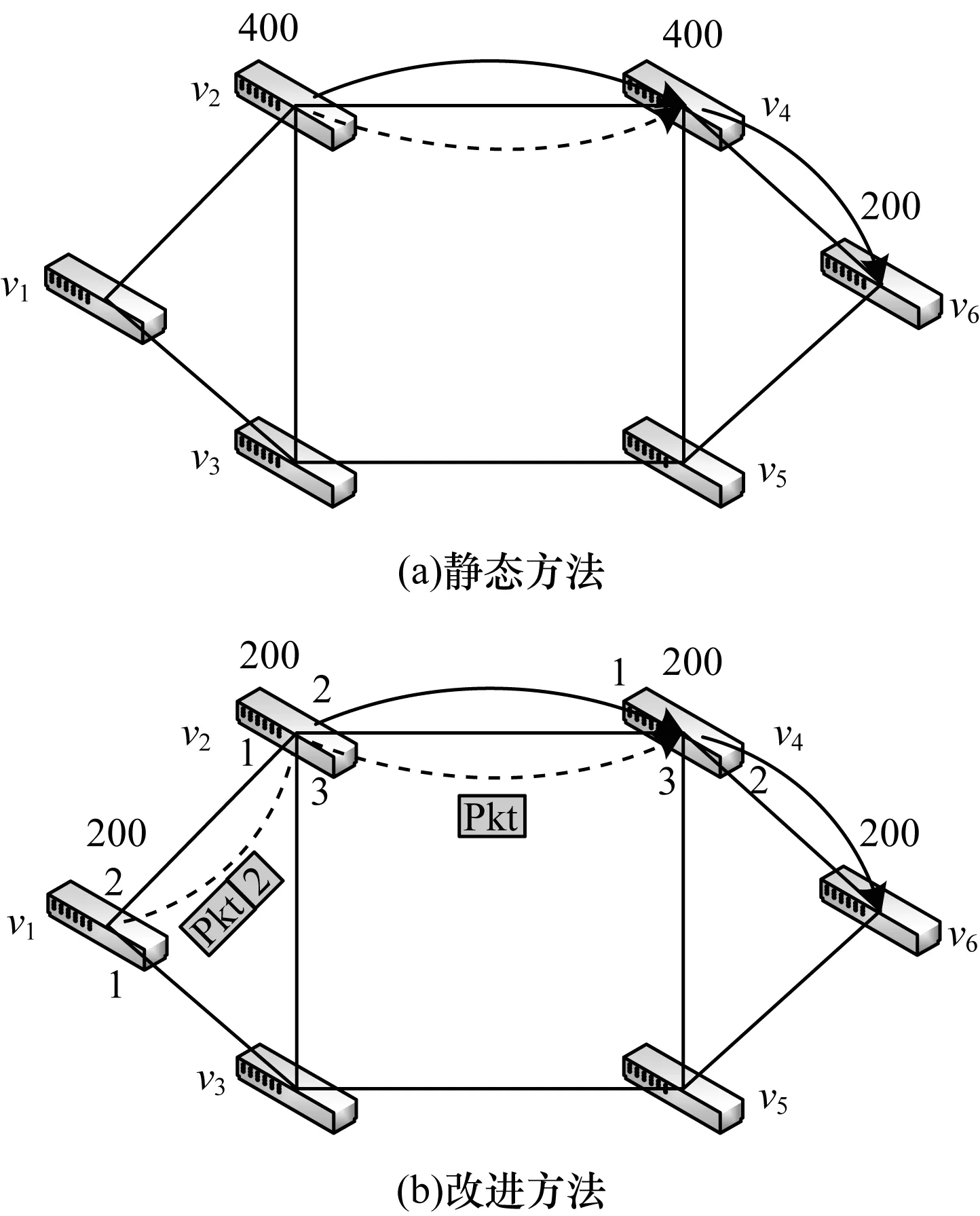
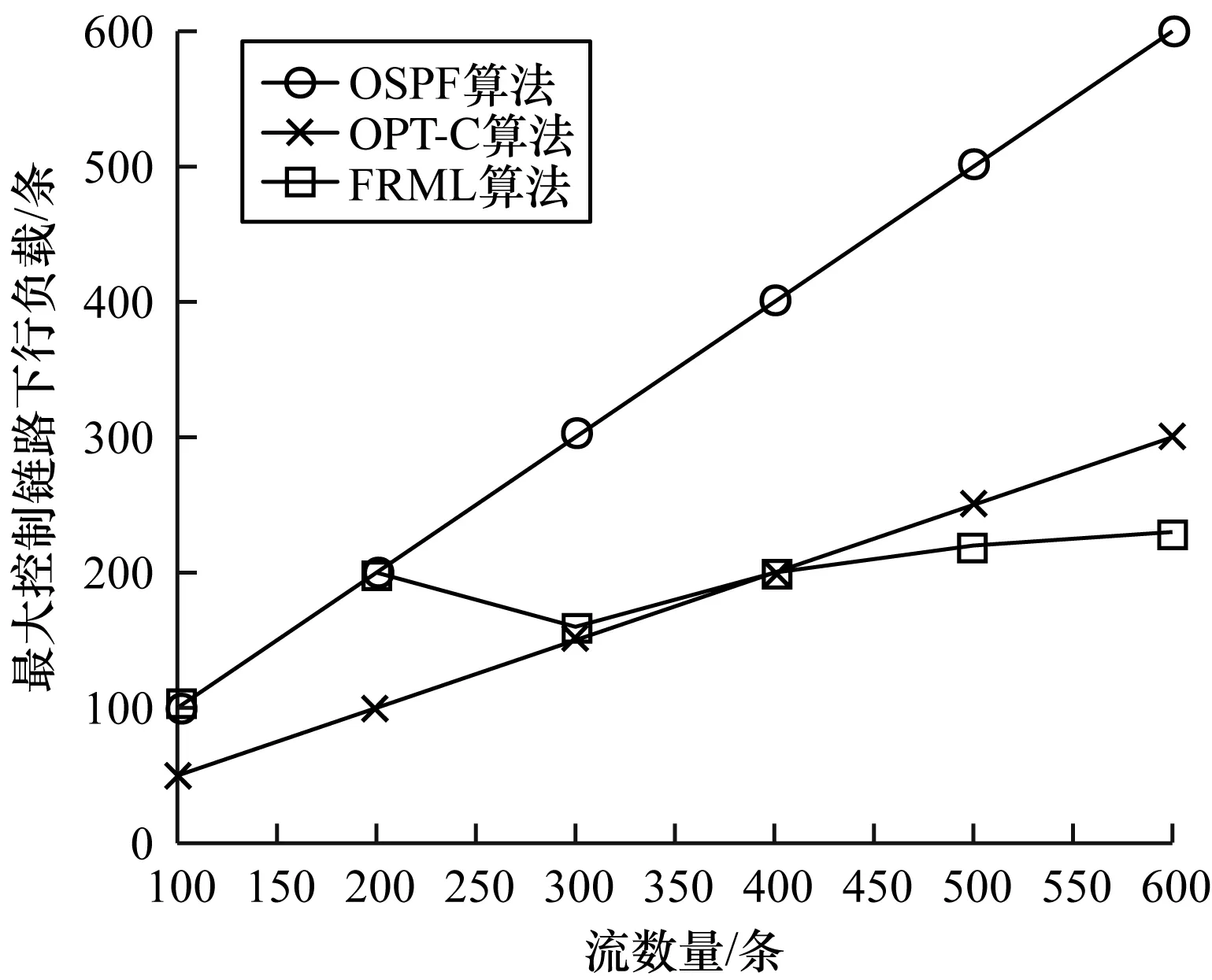
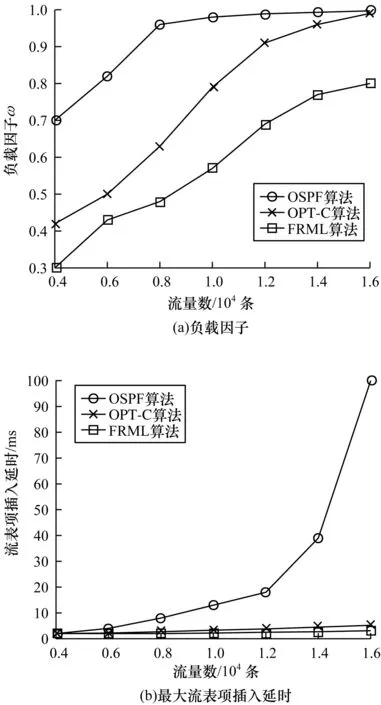
1)底层网络。本文考虑将软件定义网络结构用一个三元组来表示,即S(U,V,E)。其中,U={u1,u2,…,um}代表所有控制器,V={v1,v2,…,vm}代表所有交换机,m=|U|表示控制器数量,n=|V|表示交换机数量。在多控制器SDN中,有m 2)阈值设定。对于交换机vi,用F(vi)(条)表示待下发流表数,并定义其阈值,如式(1)所示: Ri=cd(vi)·B (1) 其中,B为其重定向阈值因子。对于源节点,当预计下发流表数超过阈值时,先将部分流通过通配符的方式重定向到邻居负载较低的交换机中,用Vi表示与vi距离只有一跳的所有交换机集合,pi=|Vi|。规定所有超出阈值的交换机集合为V′。当超过阈值时,将ft(vi,vij)条流量从vi重定向到vij,j=1,2,…,pi,vij∈Vi。对于路径交换机,若某一条流的路径上有交换机负载超过阈值,则启用MPLS方式进行流表下发,在路径交换机中选择n个负载最低的交换机下发流表。为方便讨论,假设所有下行链路具有相同的链路容量,即所有交换机链路容量均为cd(v)·B,则阈值可以统一表示为: R=cd(v)·B (2) 对于源节点重定向过程,为增加系统弹性,设定重定向下限T,其中T 3)链路开销。每个MPLS标签的大小为4 MB,因此,定义其额外链路开销如式(3)所示: (3) 其中,lf表示流f的路径向量,即: (4) (5) 1.2.2 优化目标与约束条件 优化目标与约束条件如下: 1)优化目标 对于本文提出的下行控制链路拥塞问题,将该问题定义为一个最优化问题,优化目标为使下行控制链路负载因子最小,交换机下行控制链路负载因子如式(6)所示: (6) ω越接近于1,证明系统总的负载越大,超过1则证明系统中待安装流表超过了系统能够承载的最大值,可能会出现系统崩溃等极其恶劣的情况。 该最优化问题优化目标如式(7)所示: minω,∀vi∈V (7) 2)约束条件 约束条件主要包括以下3种: (8) (9) 其中: (10) (3)数据链路开销约束。采用MPLS算法进行流表项下发的同时,也需要考虑可能会给数据链路带来的额外开销,每条流给数据链路带来的额外开销不得高于给定阈值C(f),则有: Inf(lf) (11) 针对下行控制链路拥塞问题,本文采用一种改进的MPLS算法进行解决,主要方法如下:1)基于OpenFlow协议周期性收集流表安装分布情况和接口状况;2)预测下一个周期的各交换机流表安装负载,将下周期可能超载的源节点交换机的流量重定向到相邻的负载较低的交换机,作为新的源节点进行路径计算;3)计算路径中如果存在下行控制链路负载超过阈值的交换机,则对该条流采用MPLS方式下发流表,选取路径中负载较低的几个交换机下发流表,借用一部分数据链路的带宽来缓解下行控制链路负载过高的问题。 针对上述提出的约束条件和优化目标,首先通过一个实例对工作流程进行说明。对于如图1所示的拓扑,参考文献[6]的数据,假设拓扑中交换机安装流表项的速度为每秒200条,在单位时间内存在两组流f1、f2先后到达交换机v2,流f1目的节点为v6,流f2目的节点为v4,两组流均包含200条子流,且f1先于f2进入系统,则进行优化前,流传输路径及下行控制链路负载如图1(a)所示。可以看出,流f1与流f2均需经过路径v2~v4,这就导致交换机v2和v4均需安装400条流表,严重超过了交换机安装速率的每秒200条,此时会导致下行控制链路拥塞,流表无法及时安装到系统中,造成流传输的延时,影响用户体验。 针对以上情况,本文提出的算法流程如图1(b)所示,首先将f2的流重定向到v1中,由v1作为新的源节点接收控制器的流表,然后控制器下发的流表为在f2的数据包中插入MPLS标签,该标签告知交换机数据从哪个端口发出,发出后交换机对本交换机对应的MPLS标签做删除处理,通过重定向和MPLS标签的方式共同作用缓解系统下行控制链路拥塞问题。可以看出,使用本文方法可以降低复用路径上的流表安装负载,且能够利用邻居节点来分担源节点的流表安装负载,付出的代价为增加数据链路的负担,如本实例减少了两个拥塞交换机上的流表安装负载,在数据链路每条流增加了(2+1)×4=12个字节的开销,单条链路每条流最多增加了2×4=8个字节的开销,相比于在两个交换机各多出200条的流表安装负载,显然拥有更好的效果。 图1 MPLS算法流程示意图Fig.1 Schematic diagram of MPLS algorithm procedure 根据系统对下一单位时间流表下发的预测,当源节点可能发生下行控制链路拥塞时,提前在交换机中安装通配符,将指定数目的流向邻居交换机进行重定向,由空闲的邻居节点作为新的源节点进行Packet-In消息的上报和流表下发节点,邻居节点间负载差距有多种情况,因此针对各种情况制定规则对流量进行重定向: 假设vi有邻居交换机vi1,vi2,…,vip∈Vi,且F(vi1) 规则1当F(vi) ft(vi,vij)=0 (12) 规则2若对于vi1,有F(vi1) ft(vi,vi1)=F(vi)-T (13) (14) ft(vi,vij)=R-F(vij),j=1,2,…,m (15) 规则5若对于vi1,有F(vi1)>R,且F(vi)-R>F(vi1)-R,即邻居节点均超载但仍有负载低于vi的节点,则: (16) 规则6若对于vi1,有F(vi1)>R,且F(vi)-R ft(vi,vij)=0 (17) 重定向算法如下: 算法1源节点流重定向算法 输入重定向阈值R,邻接矩阵V,系统内节点负载 输出重定向流量数和方向 1.∀vi∈V & F(vi)>R 2.for vij∈Vi,i=1,2,…,n 3.if F(vij) 4.if F(vi)-T 5.ft(vi,vi1)=F(vi)-T 6.else 7.ft(vi,vij)=R-F(vij) 8.end if 9.else if F(vi)-R>F(vi1)-R 11.end if 利用MPLS算法下发流表,具体实现过程如图2所示,MPLS算法将路径信息作为额外标签封装在原始数据包中,这样就只需在源节点和路径上某几个交换机节点下发流表项对标签信息进行封装,其他交换机只需要读取MPLS中的端口信息,将数据包从相应的端口发送出去即可,这种方法可以利用数据链路的带宽来缓解交换机中下行控制链路资源紧张的情况。 图2 MPLS算法实现过程Fig.2 Implementation process of MPLS algorithm 对于需要利用MPLS算法进行传输的流,最主要的是选取路径中下发流表的交换机,本文采用贪心算法,每次选取一个路径上负载最低的交换机作为中间节点,直到没有负载低于阈值R的交换机可选,或者MPLS算法的路径开销低于某个阈值C’为止,然后进行流表下发并进行下一条流的计算,具体算法流程如下: 算法2MPLS算法交换机选择 输入流路径向量lf,路径上交换机负载F(vi) 初始化下发交换机集合Vd={vs} 输出下发交换机集合Vd 1.对路径lf上交换机按负载大小排序,F(v′1) 2.for v′i∈lf,i=1,2,…,n 3.if F(v′i)>R or Inf(lf) 4.break 5.else add v′iin Vd 7.end if 8.end for 对于每一个单位时间的流表安装请求,本文算法计算过程如下:1)检测交换机超载情况;2)遍历源节点的邻居节点,并选择合适的邻居节点对流量进行重定向;3)选择流量进行MPLS标签安装。其中当检测到交换机超载时,便会启动后续过程,遍历超载交换机的所有邻居节点,进行一次重定向,之后会选择重定向后的流进行MPLS算法的交换机选择,最坏的情况是将所有交换机都选择一遍。因此,可以得到本文算法复杂度为O(m+n)。 对比算法选取了两种算法,第一种是OSPF路由算法[17],其运用经典的最短路由算法,另一种是文献[15]提出的OPT-L算法,即对LRD问题进行线性松弛后的线性最优解算法。 本文实验在mininet[18]平台上搭建了仿真实验环境,利用Ryu[19]开源控制器软件作为系统控制平面,选取了一个拥有100个交换机节点和50个终端节点的校园网络拓扑[20],设定该网络数据链路容量为100 Mb/s,运用随机算法模拟系统中随机到达的流量。为减少随机算法对模拟结果造成影响,对每组实验进行50次,取平均值得到最终的仿真结果。仿真实验平台为Inter Core i7-8700 3.2 GHz CPU,16 GB内存,Linux系统个人电脑。采用Java语言搭建仿真环境,并借助Matlab对实验结果进行分析。 首先对3种算法的系统最大下行控制链路负载进行对比,最大下行控制链路负载就是系统中负载最大的交换机的负载,可以衡量系统中负载最大的点的情况。仿真结果如图3所示,可以看出,随着系统中某个交换机到达的流数量增加,OSPF算法的交换机最大下行控制链路负载随之增加,并很快超过了系统最大每秒安装速率,造成严重的拥塞问题。OPT-C算法可以通过重定向方法缓解系统中最大下行控制链路负载,但是其重定向单元为宏流,即某一组流,因此受限于宏流的大小,只能将负载降低到OSPF算法的50%,且依然会使系统中负载超过安装速率,造成较大的下行控制链路负载。 图3 最大下行控制链路负载Fig.3 Maximum downlink control link load 本文FRML算法在系统负载到达阈值200前,与OSPF算法负载一致,但是并未超过每秒负载上限。随着系统中流量数增加,重定向及MPLS标签机制触发,可以将系统中负载降低到阈值200附近,并保持及其缓慢的增长速度,可以看到在负载较低时,FRML算法可以不进行任何操作,降低系统开销,当超过阈值时,FRML算法可以显著降低系统负载,且效果优于OPT-C算法。 下文对数据链路负载因子ω与系统最大流表项插入延时进行仿真,仿真结果如图4所示。 图4 负载因子与最大流表项插入延时对比Fig.4 Comparison of load factor and maximum flow table insertion delay 图4(a)表示负载因子与系统中总流量数之间的关系,随着系统中流量数增加,系统中出现某些交换机严重超载的情况,OSPF系统中负载显著增加,最后几乎达到系统满载,严重影响系统性能,OPT-C系统可以通过流重定向机制改善OSPF系统的负载,但是系统中流表下发数目并未减少,而只是将某些交换机的负载转移到了其他空闲交换机,因此随着流量数增加,系统中负载最终也会达到满载。FRML算法从根本上减少了下发到系统中的流表数,能够变相增加系统容量,大大减缓达到满载的速率。 图4(b)表示系统中最大流表插入时延与系统中流量数的关系。随着系统中流量数增加,OSPF系统逐渐达到满载,拥塞导致流表项插入延迟指数增长,造成严重的延迟现象。而OPT-C和FRML两种算法均使用了重定向算法,不会造成某个交换机流表插入延时的显著增加,但是FRML需要插入的流表数相对较少,因此FRML算法流表项插入延时相比于OPT-C算法有一定的优势。 最后对系统中的网络吞吐量进行仿真,结果如图5所示,可以看出OSPF算法很容易出现单个交换机负载过高,严重影响整个系统的负载能力,限制网络吞吐量。OPT-C算法可以缓解单个交换机负载能力,但是系统总的负载能力仍然没变,在流量增加到一定限度时仍然会达到吞吐量瓶颈,本文提出的FRML算法减少了系统中下发流表项数,使得系统中有限的下行控制链路容量可以容纳更多的流表项下发,因此可以进一步增加网络吞吐量及系统的容量。 图5 网络吞吐量仿真结果Fig.5 Simulation results of network throughput 本文针对SDN系统中下行控制链路负载较大的问题,通过重定向和下放MPLS标签的方法,缓解了源节点交换机与路径交换机存在的流表项插入速率较低导致的系统性能下降,并在SDN实验平台上进行了验证,结果表明,与传统的OSPF、OPT-C算法相比,该算法链路负载分别降低近60%、20%,最大表项插入延时方面相比于OSPF算法降低了近90%,略优于OPT-C算法,同时相比于OSPF算法和OPT-C算法网络吞吐量分别增加了近200%和30%。本文假设条件为流表容量充足条件下的流表下发策略,未考虑流表容量不足的情况会对本文实验造成的影响,下一步将针对更复杂的情况进行探讨,并在实际实验平台中验证本文算法的高效性与实用性。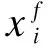


2 算法设计
2.1 源节点重定向算法

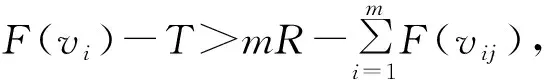
2.2 MPLS算法

2.3 算法复杂度分析
3 实验验证
3.1 性能指标与对比算法

3.2 仿真实验

4 结束语

