SWAN模型中不同破碎指标对波浪模拟的影响

丁 磊 ，张 鑫，张 晶

(1. 天津科技大学海洋与环境学院，天津 300457；2. 天津市海洋环境与修复技术工程中心，天津 300457；3. 中交水运规划设计院有限公司，北京 100007)

利用 SWAN模型进行近岸波浪模拟时，波浪破碎的描述对结果有显著影响，因此，选择合适的破碎指标使得模型能够较为合理地反映破碎前后的波高变化便具有重要的意义．

最常用的破碎指标为常数模式，通常取值为0.73[1](以下简称 BJ78)．然而，仅用常数来计算波浪破碎往往存在缺陷．因此，后来的研究者考虑了更多影响波浪破碎的因素．Nelson[2]根据一系列坡度小于0.01的实验室试验测得的波高值和水深之比的包络线提出了破碎指标与坡度之间的关系(以下简称NE87)．Ruessink等[3]基于现场观测建立了破碎指标与相对水深的线性关系(以下简称 RU03)．Goda[4]通过分析其他研究者的波浪破碎试验数据提出考虑坡度影响的破碎指标(以下简称 GO70)，目前在国际海岸工程界被广泛采用．2010年 Goda[5]重新对 GO70进行评估，提出了改进形式(以下简称 GO10).Salmon等[6]将坡度与相对水深结合得到破碎指标(以下简称SA15)．

申翼[7]在 GO70基础上建立了可调参数A与深水波陡的关系式，避免了人为调整系数的不便性，从而给出了新的Goda修正公式，即GOMOD15．之后，在SWAN模型中分别采用BJ78、NE87、RU03、SA15和 GOMOD15进行计算，并与试验和现场观测结果相比较，表明 GOMOD15的计算精度最高．Lin等[8]通过模型计算分别比较了 BJ78、NE87、SA15、RU03、GO10以及 Thornton等[9]1983年提出的破碎指标(以下简称 TG83)，结果表明：BJ78的不足在于平底条件下会低估局地生成波浪的有效波高，而高估外海生成波浪的有效波高；TG83由于过多计入了破波带外的能量耗散而低估了波高；RU03在浅水区的破碎指标值相对较低，从而低估了除平底外其他情况的有效波高；NE87在陡坡上的破碎指标值过大，从而会高估该条件下的有效波高；GO10在斜坡上的表现令人满意，但在平底上有较大误差；SA15显著减小了平底条件下有效波高的模拟误差，但在斜坡上的表现则不及 BJ78．于是，作者对 SA15进行改进，将其浅水条件下破碎指标与坡度的线性关系转变成非线性关系，得到 SAMOD17，从而在 SA15基础上又进一步提高了波浪谱模型在斜坡上的模拟精度．

综上，GOMOD15和 SAMOD17在波浪破碎模拟中的表现均优于 SWAN模型中可供选择的破碎指标，即 BJ78、NE87、RU03、TG83 和 SA15，然而目前尚未见关于对比 GOMOD15和 SAMOD17的工作，因此，本文将两者分别引入SWAN模型进行再比较，为今后模型使用过程中破碎指标的选择提供参考．

1 模型简介

SWAN模型是基于动谱平衡方程的第三代波浪模型[10]，综合考虑了波浪传播过程中的浅水变形、折射、绕射、底摩擦以及波浪破碎等多种因素的影响．

1.1 波浪破碎项

为了模拟波浪向岸传播过程中由于水深变浅引起的波浪破碎，SWAN 模型采用 Battjes等[1]提出的波浪破碎耗能源函数 Sdb(σ,θ)表达式，即

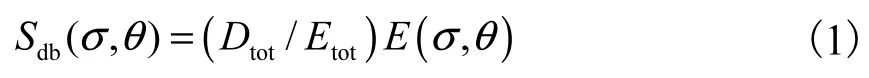
式中：σ为频率；θ为方向角；Etot为总波能；Dtot为单位面积上波浪破碎导致的能量平均损耗率；E(σ ,θ)为能量密度．

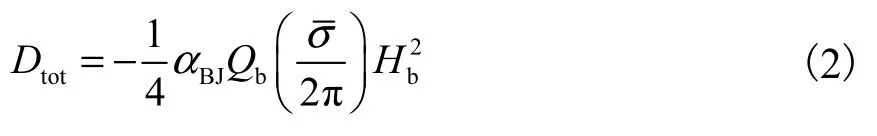
1.2 新破碎指标的引入

在SWAN模型中引入新的破碎指标 SAMOD17和GOMOD15，其具体形式如下：

SAMOD17表达式为

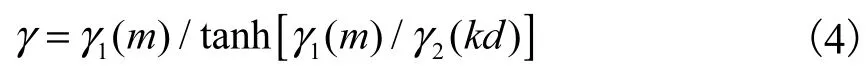
式中1γ和2γ分别与坡度m和相对水深kd(k为波数)相关，即

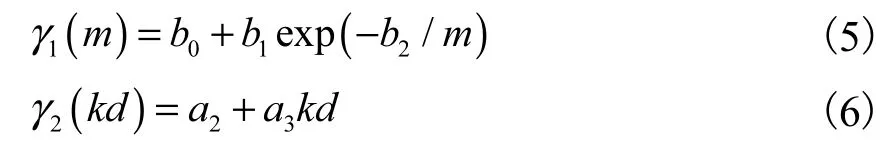
其中b0、b1、b2、a2和a3为可调参数，Lin 等[8]建议分别取值为 0.54、0.47、0.018、-8.06和 8.09，后文计算时将采用这些数值．

GOMOD15表达式为

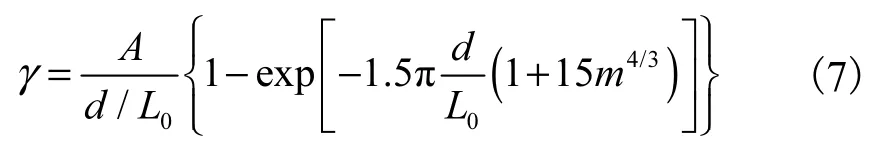
式中H0为深水波高．

2 模型验证

本文选择Bowen等[11]斜坡上的不规则波水槽试验数据进行 SWAN模型的验证．该试验的斜坡坡度为 1∶35，其布置图详见文献[11]．选择正向入射，均方根波高为0.07m，谱峰周期为2.0s的波浪条件(以下简称 BK7cm)，入射波浪处的水深为 0.44m，波浪谱取为JONSWAP谱，由此得到深水波陡为0.0187，则 A = 0 .148．

另外，为了定量反映 SWAN模型模拟结果与实测波高值之间的拟合程度，本文采用 Wilmott[12]提出的用来衡量模型精确性的统计方法

图 1显示了均方根波高(Hrms)随水深(d)变化的实测值与 SWAN模型分别采用 SAMOD17和GOMOD15所得计算值的比较结果．需要说明的是，SWAN模型输出的波高为有效波高Hs，文中采用的关系式[13]将其转换成均方根波高Hrms．结果表明，两种破碎指标对应的结果均较好地反映了波浪破碎前后波高演变的全过程，可用于下文研究．同时，使用 SAMOD17计算得到的Skill值为0.96，而GOMOD15 对应的Skill值则达到0.98，更接近于1.0．

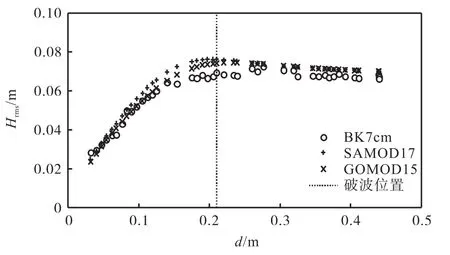
图1 均方根波高实测值与模拟结果的比较Fig. 1 Measured and simulated root-mean-square wave height

3 结果与分析

为了进一步比较SAMOD17和GOMOD15对波浪模拟的影响，本文还收集了其他4组实验室试验和现场观测数据．第 1组数据来自常艳玲[14]关于波浪水槽中的不规则波试验(以下简称 CYL)，第 2组数据来自Wood等[15]关于LWI波浪水槽中的不规则波试验(以下简称 LWI)，第 3组数据是从 Wu等[16]文献中选取的1980年2月2日现场观测数据(以下简称NSTS-2.2)，第4组数据是从Ris等[17]的文献中提取的荷兰哈灵水道海区的观测数据(以下简称Haringvliet)．

3.1 实验室试验

CYL的试验段地形主要由一段坡度为 1∶15的斜坡连接一段平底构成，试验布置图见文献[14]．该试验的波浪为正向入射，选取的入射有效波高为0.115m，有效周期为1.4s，入射波浪处水深为0.45m，平底处水深为 0.20m，波浪谱取为 JONSWAP谱，由此得到深水波陡为 0.054，则 A = 0 .166．由试验结果可知，此时的波浪破碎发生在平底处，从而可以用来检验 SAMOD17和 GOMOD15在平底地形上的表现．有效波高(Hs)随与造波机距离(l)变化的实测值与分别采用SAMOD17和GOMOD15的模拟结果的比较如图2所示．

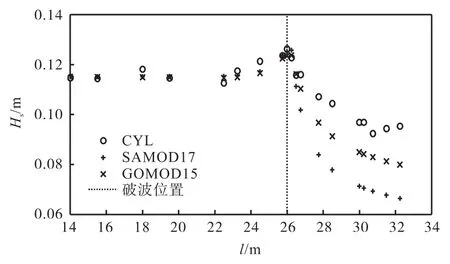
图2 有效波高实测值与模拟结果的比较Fig. 2 Measured and simulated significant wave height

结果表明，在平底条件下，波浪破碎发生后，SAMOD17与 GOMOD15的结果差异较为显著，而采用 GOMOD15的模拟结果更接近实测值．从Skill的数值来看，使用 SAMOD17 计算得到的Skill值为0.78，而GOMOD15的则达到0.91，更接近于1.0．

对于 LWI，其斜坡是由 4个坡度近似为 1∶12、1∶20、1∶30、1∶∞的坡连接而成的，试验布置图详见文献[15]．该试验的波浪为正向入射，入射有效波高为 0.17m，谱峰周期为 1.7s，入射波浪处的水深为0.7m，波浪谱取为JONSWAP谱，由此得到深水波陡为 0.07，则 A = 0 .171．有效波高(Hs)随与造波机距离(l)变化的实测值与分别采用 SAMOD17和GOMOD15的模拟结果的比较如图 3所示．结果表明：实测有效波高在离造波机大约 57m 的位置开始逐渐减小，并且在该位置之前，采用 SAMOD17与GOMOD15得到的模拟结果与实测值都较为接近.在这个位置之后，随着坡度的逐渐变缓，SAMOD17与 GOMOD15的结果差异逐渐显著，而采用GOMOD15的模拟结果更接近实测值．这从Skill的数值也可以看出，使用 SAMOD17 计算得到的Skill值为0.93，而GOMOD15对应的Skill值则达到0.98，更接近于 1.0，同时结合 BK7cm和 CYL的结果，说明引入 GOMOD15破碎指标的 SWAN模型较SAMOD17可以更好地模拟实验室尺度的不规则波浪的破碎过程．

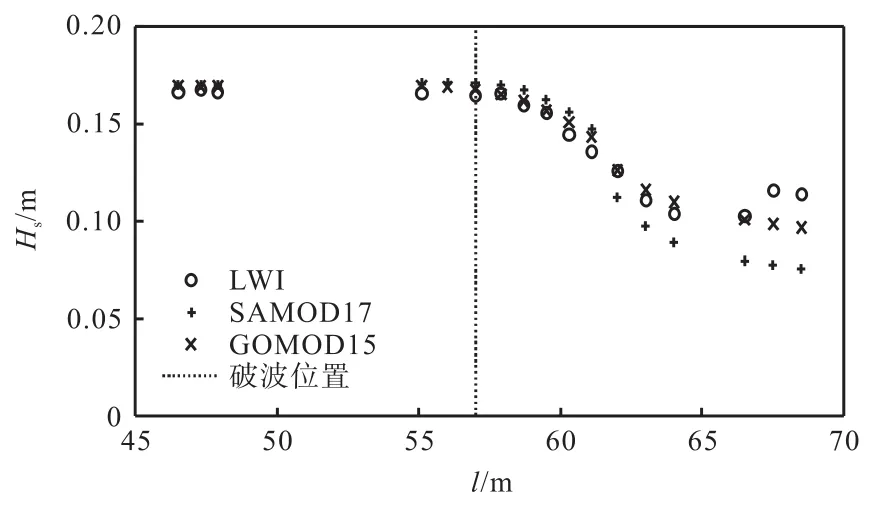
图3 有效波高实测值与模拟结果的比较Fig. 3 Measured and simulated significant wave height

3.2 现场观测

对于 NSTS-2.2，观测地点位于美国加州的Leadbetter海滩，该海滩东西向分布，海滩地形和观测点位置如图 4所示，图中横轴(x)表示沿岸距离，纵轴(y)为离岸距离．

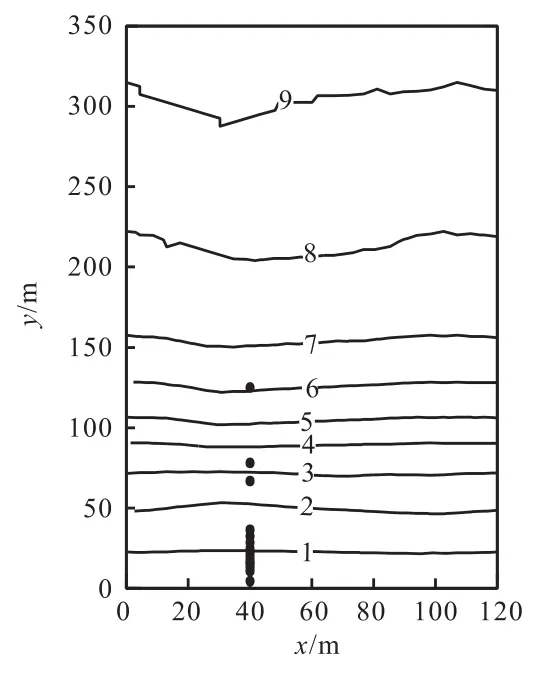
图4 Leadbetter沙滩1980年2月的近岸地形Fig. 4 Nearshore bathymetry at Leadbetter Beach in February 1980

该海滩外海大约9m水深处的波浪条件如下：入射均方根波高为 0.37m，谱峰周期为 16.0s，入射角度为15.2°，波浪谱取为JONSWAP谱，由此得到深水波陡为0.0021，则 A = 0 .117．

NSTS-2.2均方根波高实测值与模型结果比较如图5所示，使用SAMOD17和GOMOD15对应的结果均与实测值符合较好，由 SAMOD17 计算得到的Skill值为 0.92，而 GOMOD15对应的Skill值则达到0.93，更接近于1.0．

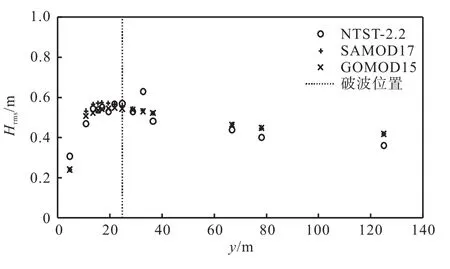
图5 均方根波高实测值与模拟结果的比较Fig. 5 Measured and simulated root-mean-square wave height

对于 Haringvliet，该海区是位于荷兰西南部的一个海湾，它的入口处有一个相对平坦的浅滩，浅滩在平均波浪方向上的坡度从 1∶500到水平(在浅滩顶部)变化．海域地形和观测点位置如图 6所示．选取1982年10月14日23:00UTC时刻的海况条件，波浪边界条件由JONSWAP谱生成，对应的波浪要素为有效波高 3.56m，平均周期 6.7s，平均波向306°，入射波浪处的水深为 16.78m，由此得到深水波陡为0.055，则 A = 0 .170．模型由定常风场驱动，设置风速为 14.0m/s，风向为300°，结合作者之前的工作[18]，其风拖曳力系数采用SWAN模型的默认选项FIT．

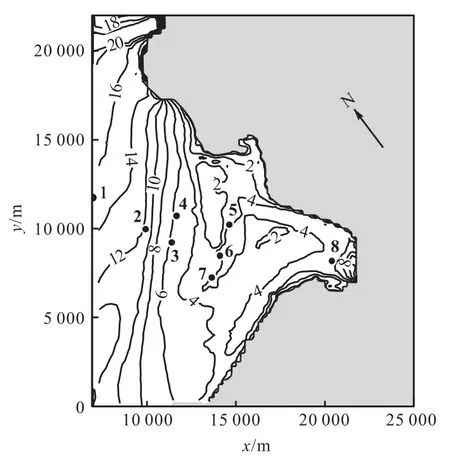
图6 海域地形Fig. 6 Bathymetry of sea area

图7显示了有效波高实测值与SWAN模型计算值的比较结果，此时由 SAMOD17 计算得到的Skill值为0.97，而GOMOD15对应的Skill值则达到0.99，更接近于1.0，即使用GOMOD15的模拟结果更接近实测值．综合 NSTS-2.2和 Haringvliet的结果，可以看到引入 GOMOD15破碎指标的 SWAN模型较SAMOD17可以更好地模拟现场条件下近岸波浪的破碎过程．

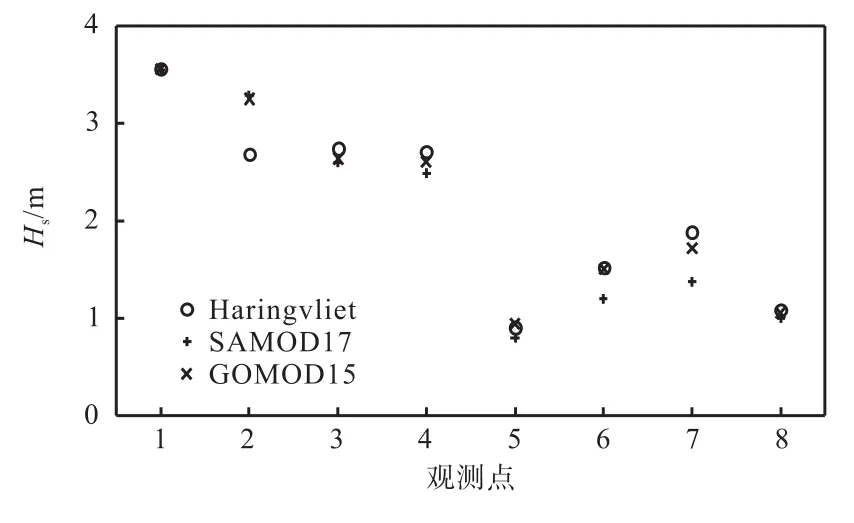
图7 有效波高实测值与模拟结果的比较Fig. 7 Measured and simulated significant wave height

4 结 语

选择经过比较目前常用的波浪破碎指标后推荐的 SAMOD17和 GOMOD15进行再比较．将两者分别引入SWAN模型，利用实验室水槽试验(包括斜坡和平底条件)和现场观测数据比较两者对 SWAN模型波浪模拟的影响．总体来看，随着坡度的逐渐变缓，SAMOD17与GOMOD15的结果差异逐渐变大，特别是在平底条件下，这种差异更为显著．同时，无论是与实验室水槽试验还是现场观测数据对比，采用GOMOD15得到的Skill值均比采用 SAMOD17得到的Skill值更接近于1.0，即GOMOD15的模拟结果更接近实测值．相比于SAMOD17，引入GOMOD15的SWAN模型可以更加合理地模拟实验室尺度的不规则波浪以及现场条件下近岸波浪的破碎过程，且不需要人为调整其参数，故在采用 SWAN模型模拟波浪破碎时推荐使用GOMOD15破碎指标．