立式曲面网板水动力及周围流场数值仿真研究

徐琦　于文明　郑建丽　梁晶晶

摘  要：该文研究了立式曲面网板在不同冲角下的水动力性能变化情况，并且对网板周围流场可视化及表面压力分布可视化进行了探究。结果表明，当网板雷诺数在5.2×104～9.5×104区间时，升力系数、阻力系数和力矩系数随雷诺数增大基本保持不变，而升力系数和力矩系数随冲角增大呈先增大后减小趋势;阻力系数随冲角增大一直增大。升力系数的试验值和模拟值随冲角增大均呈先增大后减小趋势，阻力系数的试验值和模拟值随冲角增大呈一直增大趋势，升阻比的试验值和模拟值随冲角均呈先增大后减小趋势。CFD结果显示，网板表面压力分布随冲角增大逐渐增大，而网板压力中心随冲角增大基本保持不变。

关键词：网板;水动力性能;模型试验;数值模拟;流场可视化;压力分布

中图分类号：S971.4       文献标识码：A 文章编号：2096-4706（2020）09-0064-07

Numerical Simulation Research of Hydrodynamic Force and Surrounding

Flow Field of Vertical Curved Reticular Lamina

XU Qi1，YU Wenming2，ZHENG Jianli3，LIANG Jingjing1

（1.Zhejiang Ocean University，Zhoushan  316022，China;2.South China Sea Fisheries Research Institute，Chinese Academy of Fishery Sciences，Guangzhou  510300，China;3.Fishery Machinery and Instrument Research Institute，Chinese Academy of Fishery Sciences，Shanghai  200092，China）

Abstract：This paper studies the changes in hydrodynamic performance of the vertical curved reticular lamina at different angles of attack，discusses the differences in the results of the different studies，and visualizes the flow field and surface pressure distribution around the reticular lamina. The results show that when the Reynolds number of the stencil is in the range of 5.2×104 to 9.5×104，the lift coefficient，drag coefficient and torque coefficient remain basically the same as the Reynolds number increases，while the lift coefficient and torque coefficient are first trend decreases after the increase;the drag coefficient increases with the angle of attack. The experimental value and the simulated value of the lift coefficient both increase first and then decrease as the angle of attack increases. The experimental and simulated values of drag coefficient have been increasing with increasing angle of attack. The experimental and simulated values of lift-to-drag ratio increase first and then decrease with the angle of attack. The CFD results show that the pressure distribution on the surface of the stencil gradually increases with increasing angle of attack，while the pressure center of the stencil basically remains unchanged as the angle of attack increases.

Keywords：reticular lamina;hydrodynamic performance;model test;numerical simulation;flow field visualization;pressure distribution

0  引  言

網板是单船拖网作业的重要属具之一，主要作用为实现网口扩张、增大扫海面积，其水动力性能的优劣直接影响渔获性能和经济效益[1]。因此，开展网板水动力性能的研究尤为重要。笔者对网板在不同冲角下水动力性能的变化进行了研究，探讨不同研究结果的差异，并实现网板周围流场及表面压力分布可视化。

在设计网板时一般须满足几项条件：一是在一定拖速内保证网口的扩张基本不变;二是要求网板具有较高扩张力和较低阻力;三是要求网板稳定性好;四是要求网板使用简单，维修方便[2]。Park等[3]利用水槽试验分析了不同弯曲度的立式曲面网板水动力性能，得到弯曲度为15%时升力系数最大，表层作业时其最适冲角范围大于底层作业。现代拖网网板已有很多改进，包括采用新的结构形式和新型材料改进网板水动力性能，而日本渔业研究者对立式曲面网板进行了改进，采用不同的曲面形状，使得较原型网板曲度减小，适宜冲角范围增大，阻力降低，广泛应用于大、中型单船拖网渔业中[4]。目前为止，在我国远洋渔业中立式曲面网板仍有较高的使用率。因此，开展对立式曲面网板水动力性能的研究，对优化和开发新型网板具有十分重要的意义。

目前水槽模型试验已成为研究网板水动力性能的标准方法，其具有试验过程便于观察、试验条件可控的优点，研究者可以将实物网板按照尺度比例制作模型进行性能测试，而不需要制作出实物网板进行海上实测，这样节省了大量的人力和财力。模型试验虽是测量网板水动力性能标准的方法，但在试验过程中消耗费用较多，并且需要精密的仪器[5]，而随着计算机技术的发展，数值模拟技术被广泛使用，计算流体动力学逐渐被渔业研究者应用于网板水动力性能研究中，其中FLUENT分析方法具有先进的求解技术，可以快速准确地求解出CFD结果。Xu等[6]对比了V形网板的水槽试验和数值模拟结果，发现两种研究结果吻合较好，最优型的网板结构为展弦比0.49，板面折角17°。Leifsson等[7]在使用CFD数值模拟技术研究立式曲面网板水动力性能时发现传统的求解模型计算需要大量迭代次数，耗时太多，因此对模型算法进行了优化。利用模型试验和数值模拟研究网板水动力性能已成为目前渔业学者的研究思路，通过对比两种研究方法的结果即可互相验证，也可弥补相互的缺点。

本文利用水槽模型试验和CFD数值模拟方法研究立式曲面网板在不同冲角下水动力性能的变化，并对比两种研究方法的结果差异性，提出科学的建议。同时，利用CFD数值模拟技术实现网板周围流场可视化，直观地分析网板水动力性能的变化，显示出网板在水中所受到的压力分布。

1  材料与方法

1.1  网板水动力特性计算公式

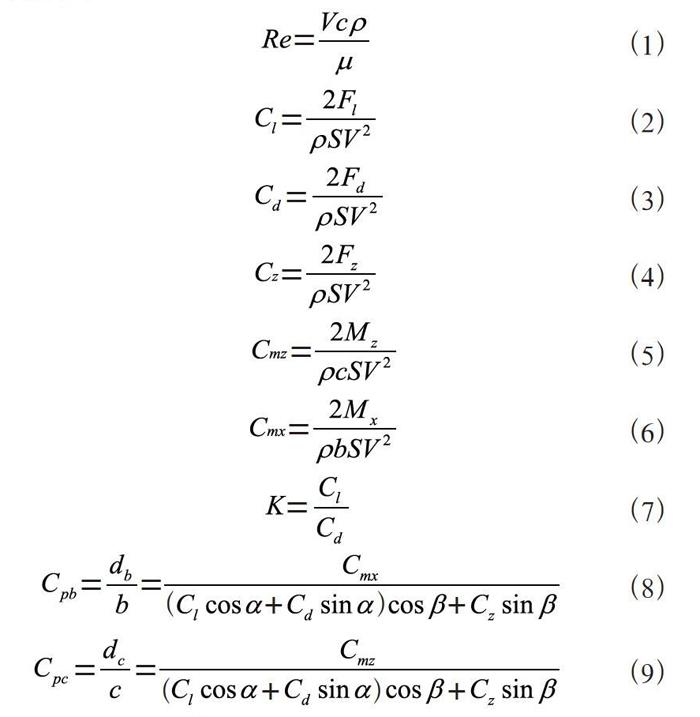
网板水动力特性的参数主要包括雷诺数Re、升力系数Cl、阻力系数Cd、垂直系数Cz、滚转力矩系数Cmx、纵向力矩系数Cmz、升阻比K、翼展到压力中心距离的压力中心系数Cpb、翼弦到压力中心距离的压力中心字数Cpc，计算公式如下所示：

式中：c为网板翼弦（m），ρ为流体密度（kg/m3），b为网板翼展（m），V为流速（m/s），μ为流体动力粘性系数（kg/m/s），Fl为网板扩张力（N），Fd为网板阻力（N），Fz为网板垂直扩张力（N），Mz为纵向力矩（N·m），Mx为滚转力矩（N·m），S为网板面积（m2），db为网板顶端到压力中心距离（m），dc为网板翼端到压力中心距离（m），α为网板冲角（°），β为网板倾角（°）。

水槽模型试验中，当流速增大至某一特定值后，升力系数或阻力系数基本保持不变即进入自动模型区。本次试验所使用升力系数、阻力系数和垂直系数均为进入自动模型区后测量值的平均值。

1.2  水槽试验条件设置

立式曲面网板模型如图1所示，比例尺为1：20，展弦比为1.65，网板外侧圆弧相对弯度38%，内侧圆弧相对弯度23%。

水槽模型试验在东海水产研究所循环水槽完成，试验水槽尺寸长1.8 m，宽0.5 m，水深0.5 m，最大流速为2.5 m/s。三分力传感器为日本共和电业制造的LSM-B-500NSA1-P型传感器，量程500 N，精度0.1%，记录的测量值为水流稳定后20 s内的平均值。流速计为螺旋式，由日本计测研株式会社生产。网板模型位于水槽中部，通过连接杆与三分力传感器连接，如图2所示。通过调节三分力传感器下端转轴可以改变网板模型的冲角。水槽模型试验中流速设置为50 cm/s、60 cm/s、70 cm/s、80 cm/s、90 cm/s，网板冲角为0°～50°，其中在0°～15°和30°～50°范围内时以5°为间隔，15°～30°之间设置为15°、18°、20°、22°、25°、27°和30°。水槽试验中水温为20 ℃，水密度为998.2 kg/m3，粘性密度为1.011×10-3 kg/（m*s）。

1.3  数值模拟条件设置

数值模拟通过ANSYS 15.0软件中的FLUENT完成[8]。数值模拟计算中使用有限体积法（Finite Volume Method，FVM）对Navier-Stokes方程进行离散。有限体积的求解方法采用SIMPLE算法，是一种压力修正的算法，通过在交错网格的基础上计算压力场，而后求解动量方程。FLUENT求解中离散格式设置为压力二阶格式、动量方程为二阶迎风格式。湍流模型选择可实现k-ε模型[9]（Realizable k-ε），其具有既满足对雷诺应力的约束条件，又可以在雷诺应力上保持与真实情况湍流一致的优点。边界层设置中使用增强壁面函数，加强了边界层的网格密度，提高模型的计算精度。模拟计算区域如图3所示，模拟计算区域与实际水槽规格一致，尺寸为1 800.00 mm*500.00 mm*500.00 mm。

网板冲角22°时数值模拟计算中局部区域和网板周围网格划分如图4所示，网格划分全部为四面体网格，最大网格尺寸为50.00 mm，最小网格尺寸為0.61 mm。网板边界层周围第一层网格厚度为5.1×10-2 mm（y+≈1），通过从网板表面向外膨胀15层，以1.2为增长率增强边界层网格密度。

模拟计算区域总网格数为1.9×106，节点数为6.4×105。数值模拟计算区域边界条件设置如图5所示，沿X轴方向的水流速度为0.5 m/s，湍流强度为5%，湍流粘性率为10，速度入口为0.5 m/s，压力出口为0 Pa，所有网板外壁面和所有水槽内壁面均设置为固定无滑移条件。

2  结果与分析

2.1  雷诺数与网板水动力系数的关系

水槽模型试验中将测量值代入网板水动力特性计算公式（1）—（6）得到网板升力系数、阻力系数、力矩系数与雷诺数和冲角的相互关系如图6所示。由图可知，不同冲角条件下升力系数Cl随雷诺数增大基本保持不变，在一定雷诺数条件下，升力系数Cl随冲角增大呈先增大后减小趋势，在冲角25°时达到最大。阻力系数Cd随冲角增大呈一直增大趋势，在冲角不变条件下隨雷诺数增大基本保持不变。在冲角0°～25°之间，力矩系数Cmx随冲角增大逐渐增大，在25°～50°之间，随冲角增大逐渐减小。力矩系数Cmz随冲角增大呈先增大后减小的趋势，在冲角30°时达到最大。升力系数、阻力系数和力矩系数在一定冲角下随雷诺数增大基本保持不变，因此可认为当雷诺数为5.2×104～9.5×104时，在设置的流速和冲角条件下进入自动模型区。

2.2  模型试验和数值模拟结果对比分析

立式曲面网板的升力系数、阻力系数和升阻比与冲角相互关系的试验值和模拟值对比结果如图7所示。

由图可知，试验值和模拟值的升力系数Cl均随冲角增大呈先增大后减小趋势，均在临界冲角25°时达到最大值，分别为1.45和1.59，当冲角大于临界冲角后升力系数值急剧下降，两种方法研究结果在冲角小于25°时差异较大，在冲角大于25°后差异较小，升力系数的模拟值始终大于试验值。阻力系数Cd的试验值和模拟值均随冲角增大逐渐增大，在冲角18°～22°之间两种方法的结果偏差较大，在冲角小于15°时吻合较好，试验值在冲角大于27°后有明显增大趋势，阻力系数的模拟值也始终大于试验值。升阻比K的试验值和模拟值随冲角均呈先增大后减小的趋势，其值均在冲角15°时达到最大，分别为3.25和2.93，其中试验值在冲角25°时又明显增大，可能原因为试验中出现的操作误差。升阻比的试验值和模拟值在冲角大于27°后吻合较好，在冲角10°～25°之间偏差较大，适宜的工作冲角范围均为10°～22°之间，其中试验值始终大于模拟值。总之，立式曲面网板升力系数、阻力系数和升阻比的试验值和模拟值偏差较小，证明了数值模拟的准确性。

2.3  网板周围流场可视化及表面压力分布

立式曲面网板在不同冲角下网板中心平面周围流场分布如图8所示。图中水流方向为从左至右，初始流速为0.5 m/s。由图8可知，网板外侧箭头指向部分流速均大于0.6 m/s，内侧圆形标示部分流速均小于0.5 m/s，由于外侧流速增大，压力减小，内侧流速减小，压力增大，导致在网板内外两侧形成压力差，从而产生网板升力，图中箭头指向部分随冲角增大呈先增大后减小趋势，在冲角25°时达到最大，这与模型试验结果相符合。网板后部矩形标示部分流速为负值，表示在该处形成涡旋，产生涡旋的主要原因为水流经过网板背部时在网板表面形成一层很薄的边界层，随着流速的增大水流开始逐渐离开网板表面，造成边界层分离情况，由于边界层分离时粘性力的存在，分离后会在后部区域产生涡旋，形成压差阻力，随着冲角增大该区域面积增大，表明阻力值逐渐增大，与模型试验结果吻合。随着冲角增大网板左侧流速衰减区逐渐减小，主要原因是随着冲角增大，水流与网板接触面积逐渐增大，降低了流速减弱的程度。

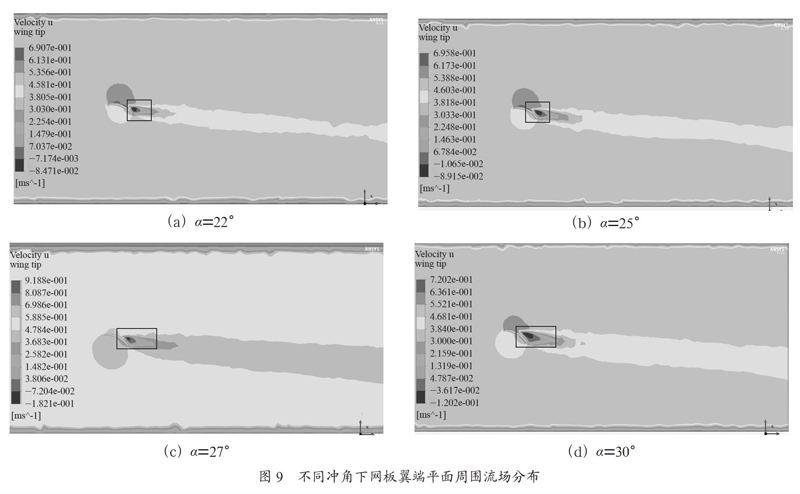
不同冲角下网板翼端平面周围流场分布如图9所示。由图9可知，网板背部产生的边界层分离点随着冲角增大逐渐向网板前端移动。网板翼端尾部矩形标示部分流速为负值，是水流与网板表面分离时形成的翼端涡，其随着冲角增大逐渐增大。网板前端流速衰减区随着冲角增大逐渐增大，后端流速衰减区随着冲角增大明显变宽。

在不同冲角条件下网板表面压力分布如图10所示，随着冲角增大网板表面压力分布逐渐增大，主要原因为冲角增大后网板与水流的接触面积增大，导致网板表面压力增大区域也逐渐增大，而网板压力中心的压力随冲角增大基本保持不变。

3  讨论

3.1  网板周围流场可视化

本文利用水槽模型试验和数值模拟研究了立式曲面网板水动力性能的变化，并对比分析了两种方法得到的研究结果，最后利用数值模拟实现了网板周围流场可视化，为今后网板的性能的研究提供了科学依据。关于网板水动力性能的研究国内外已屡见不鲜，而利用可视化手段研究网板周围流态分布还较少，目前主要实现网板周围流场可视化的方法主要有三种：线条法[10]、气泡法[11]和数值模拟，其中线条法是指将轻柔线条一端固定在网板表面，根据线条另一端在水流中所呈现出的姿态来判断网板周围的流态;气泡法指将水槽中的水通电，电解产生氢气泡，气泡随着水流经过网板后流态发生改变进而判断流态的分布情况。但线条法和气泡法只能对网板周围流场进行定性的研究，不能精确地显示网板周围流态的速度场。数值模拟技术具有高效、低成本等优点，可将网板周围流场精确地描述出来，因此利用数值模拟技术研究网板周围流态分布与网板水动力性能的关系，即可以掌握网板周围流态分布变化的原因，也可为后续网板的优化与设计提供直观的科学依据。

3.2  模型试验和数值模拟结果比较

网板的升力系数和阻力系数数值模拟结果均较水槽模型试验结果高，其主要可能由两个方面的原因导致：一是数值模拟在构建网板模型时未考虑摩擦力，使得数值模拟测试值偏高;二是因为在水槽模型试验中水流的不稳定性造成网板的震荡，使得测量水动力性能的仪器产生误差。网板模型试验时尺度比的大小会直接影响试验结果的准确性，因此在今后网板模型试验中应选择合适的模型尺度比，尽量降低模型的尺度效应对试验结果的影响。

3.3  网板开发研究趋势

网板在拖曳过程中多数情况下会存在倾斜的状态，网板在内倾状态下有利于增加稳定性并能够顺利越过障碍物，但不能内倾过大，会破坏平衡状态，造成起浮。同时网板正常工作状态也存在后倾，这样安装有利于越过障碍物。网板曳行时也会不同程度地受到外力的干扰，也可能会导致网板出现倾斜的情况，而不同的倾斜程度对水动力性能有一定影响，因此今后可开展不同倾斜程度对网板水动力性能的影响研究。影响网板水动力性能的因素除网板自身结构参数外，还有作业方式和作业海区底质类型等因素，在实际生产作业中，海底对网板的水动力性能有较大影响。本文利用模型试验和数值模拟研究立式曲面网板水动力性能的过程中，由于尽量避免无关因素影响网板性能测试数据的准确性，忽略了海底底质对网板水动力性能的影响，而且模型试验中模拟海底底质也是非常困难的，但随着计算机技术的发展，在数值模拟中可利用离散单元法建立模拟海底，通过设置海底底质黏土的材料和粘度指数来实现不同海底底质的类型，并通过连接力模型将海底与网格化的网板整合进行求解计算[12]。因此，今后研究网板水动力性能中可引入分析不同海底底质对网板水动力性能的影响。

4  结  论

立式曲面网板的水动力性能参数在进入自动模型区即雷诺数为5.2×104～9.5×104区间内时变化趋势为：升力系数的试验值和模拟值随冲角增大均呈先增大后减小趋势。阻力系数的试验值和模拟值随冲角增大呈一直增大趋势。升阻比的试验值和模拟值随冲角均呈先增大后减小趋势。

由立式曲面网板周围流场分布可知，网板升力随冲角增大呈先增大后减小趋势，在冲角25°时最大。网板压差阻力随冲角增大呈一直增大趋势。网板背部产生的边界层分离点随冲角增大逐渐向网板前端移动。网板翼端尾部形成明显的翼端涡，其随冲角增大逐渐增大。网板前端流速衰减区随冲角增大逐渐增大。网板表面压力分布随冲角增大逐渐增大，而网板压力中心随冲角增大基本保持不变。

参考文献：

[1] 张勋，王明彦，徐宝生.拖网网板型式、结构与性能的研究与应用进展 [J].中国水产科学，2004，11（z1）：107-113.

[2] 孙满昌.海洋渔业技术学 [M].北京：中国农业出版社，2005.

[3] PARK C D，MATUDA K，HU F，et al. Hydrodynamic Characteristics of Cambered Plates in Free Stream and near the Bottom [J].Nippon SuisanGakkaishi，1993，59（4）：627-632.

[4] 刘健，黄洪亮，陈帅，等.小展弦比立式曲面网板的水动力性能 [J].水产学报，2013，37（11）：1742-1749.

[5] 王锦浩，张勋，王明彦，等.矩形V型曲面网板水动力性能的研究——Ⅱ展弦比、缝口位置、缝口宽度对网板水动力性能的影响 [J].中国水产科学，2004，11（z1）：9-13.

[6] XU Q C，HUANG L Y，ZHAO F F，et al. Study on the hydrodynamic characteristics of the rectangular V-type otter board using computational fluid dynamics [J].Fisheries Science，2017，83（2）：181-190.

[7] LEIFSSON L，HERMANNSSON E，KOZIEL S. Optimal shape design of multi-element trawl-doors using local surrogate models [J].Journal of computational science，2015，10：55-62.

[8] 凌桂龙.ANSYS Workbench 15.0从入门到精通 [M].北京：清华大学出版社，2014.

[9] SHIH T H，LIOU W W，SHABBIR A，et al. A new k -? eddy viscosity model for high reynolds number turbulent flows [J].Computers Fluids，1995，24（3）：227-238.

[10] PARK C D，MATUDA K，TOKAI T. Surface Flow Visualization of Flat Plates by Tuft Method [J].Nippon Suisan Gakkaishi，1994，60（2）：193-199.

[11] PARK C D，MATUDA K，TOKAI T. Flow Visualization around Cambered Plates Using Hydrogen Bubbles [J].Nippon Suisan Gakkaishi，1994，60（4）：485-491.

[12] JUN C W，SOHN J H，PARK S H. Effect analysis of design parameter of trawl door by considering interaction with seabed [J].International Journal of Precision Engineering & Manufacturing，2016，17（11）：1515-1522.

作者簡介：徐琦（1988—），男，汉族，吉林榆树人，渔业一级船长，中级职称，工学学士，研究方向：渔具渔法。