基于双层博弈的水、光、储综合系统分区调峰方法

朱子琪， 石晓蕊， 刘海洲， 王 瑜， 祁秋民， 王正辉

（1.中国电建集团 青海省电力设计院有限公司， 青海 西宁 810008； 2.国网青海省电力公司 西宁供电公司，青海 西宁 810003； 3.国网青海省电力公司 黄化供电公司， 青海 黄化 811200）

0 前言

随着全球能源危机和环境污染问题的日益严峻，光伏发电的应用备受关注。 然而，光伏的随机性和波动性可能影响电网运行安全和电能质量，因此要引入火电等常规电源参与对光伏发电的调节[1]，[2]。 在我国部分水资源丰富地区，拥有大量梯级水电、抽水蓄能电站等调节资源，可充分利用水电调节能力，辅以储能装置对光伏进行调节，保证电能质量和电网的安全运行[3]～[5]。

国内外学者已就水、光、储系统联合调峰问题开展了相关研究，主要针对风、光、水、火调节特性和风、光、水、火联合调峰两个方面。 文献[6]从时移电量和调峰成本两方面描述了严寒地区典型居民楼调峰能力及调峰特性。 文献[7]基于实测数据提出了不同时间尺度下新能源出力概率分布曲线，为接入新能源的电力系统生产模拟奠定基础。 文献[8]提出一种以弃风量、弃光量、弃水量最小为目标，考虑多约束条件的风、光、水、火、储联合系统优化调峰模型。 文献[9]利用电源之间的互补特性， 将新能源和常规电源打捆调峰，使新能源的送出更为平稳。

上述调峰方法为水、光、储系统的联合调峰奠定了必要的技术基础， 但涉及的经济层面较少。 针对此问题，文献[10]提出了风、光、水、火电力互补的经济补偿机制；文献[11]，[12]提出利用抽水蓄能的灵活可调节性平抑新能源波动， 并以调峰成本最低为目标进行调峰。 以上方法均属于“一站式”调峰模式，即调度中心根据计算结果直接将调度指令下发至调度实体。 随着可调节实体种类和数量增多， 调度人员无法实时掌控调度实体的调节能力， 有可能造成调度实体无力调节而引起违约。另外，“一站式”调峰模式追求总的出力平稳，且总效益最高，所得到的结果可能造成内部收益极不均衡。在梯级水电站、储能等运营主体不同的背景下，虽然“一站式”调峰模式的技术可行，但在经济上很难达到平衡[13]，[14]。

针对上述问题， 本文提出了基于双层博弈的水、光、储综合系统分区调峰方法。 首先建立水、光、储双层博弈联合调峰新模式；下层采用非合作博弈模型求取各分区代理的意愿调节曲线， 使得各分区的收益达到最大； 上层采用合作博弈理论修正下层上报调节曲线，使得水、光、储总体系统效益最大； 上层修正结果在下层上报结果的基础上进行，可以减少收益不平衡问题。

1 双层博弈调峰模式及博弈性分析

1.1 调峰模式

针对目前水、光、储联合调峰中可能存在的收益不平衡问题，提出双层博弈调峰模式（图1）。

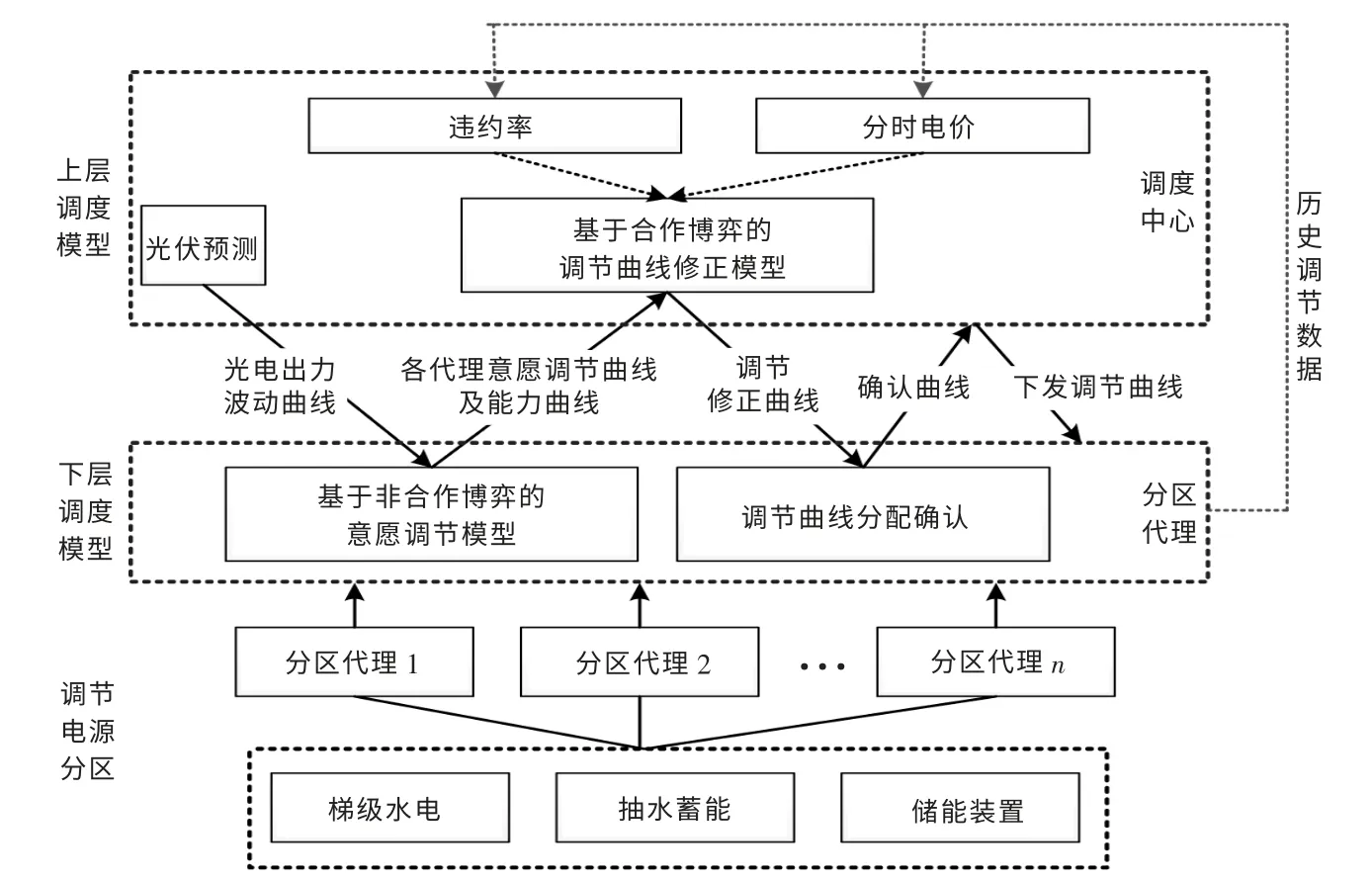
图1 双层调峰模式Fig.1 Double peaking shaving mode

该调度模式下，从光伏预测曲线到调度最终下发各代理调节曲线要经历5 个环节。

①调度中心将光伏预测曲线结果下发给各分区代理中心；

②各分区代理中心根据当前各电源调节能力约束和光伏波动曲线，基于非合作博弈求取自身最大收益的调节曲线，并将自身的调节能力曲线一起上报调度中心；

③调度中心根据光伏波动曲线和各代理初始调节曲线，对各代理中心的联合收益进行合作博弈，使整体联合收益最大，将计算得到的修正调节曲线下发至各代理中心；

④各代理中心计算判断调度中心分配的调节曲线是否超过自身调节能力，将判断结果返回调度中心；

⑤若返回结果在调节能力范围内，即技术可行，调度中心下发修正后的调节；否则，超过限值的分区取限值，其余调峰所需功率正常分配。

该模式下得到的最终解并不是经济最优解，而是一个实际可执行的可行解。

1.2 博弈性分析

当光伏实发功率与计划功率出现误差时，须要各分区电源参与调峰。 梯级水电、抽水蓄能和储能等电源的调节能力、调节灵活度及成本均不相同，各分区所包含的各类调节电源比例不同，使其调节特性和调节成本也不相同；在博弈过程中，合适的调节性能和成本会给该分区带来较大的优势；在调峰过程中，各分区电源间具有明显的博弈性。根据图1 分析可知，下层各分区代理根据光伏实发电量上报意愿调节曲线时， 为了实现自身利益最大化， 根据其他参与者的决策信息实时改变自身决策，各分区间的调峰策略相互影响，没有明显的时序性和跟随关系； 因此可采用经典的非合作博弈模型描述各参与决策者的博弈过程； 上层调度中心统筹各分区代理， 期望各分区能够相互合作，使得整体收益最大，达到最佳的社会效益；在此基础上，各参与决策者再合理分配内部收益。此时，各参与决策者之间虽有竞争，但合作关系更为明显， 且各决策者间也没有明显的时序性和跟随关系， 故可采用合作博弈描述博弈主体间的博弈过程。

2 基于非合作博弈的下层意愿调节模型

2.1 分区收益函数

针对任意分区代理i，设其在时刻t 的收益函数为Feit，市场交换价格为Seit，成本价格为Ceit，则收益函数Feit可表示为

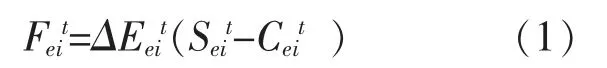
式中：成本Ceit包括一次建设成本、运维成本等；ΔEeit为t 时刻各分区调峰功率， 与当前交易价格和成本有关。

ΔEeit表达式：

式中：每个分区函数fi（·）的表达形式不同，须根据实际电网情况拟合得出。

2.2 非合作博弈调节模型

（1）模型建立

非合作博弈的核心： 各分区决策者在收益相互影响的局势中采取合适的策略， 使自身的收益最大。 设置N 个分区，则调峰过程中共有N 个自由决策者，其收益函数集合为{Fe1t，Fe2t，…，Fe（N）t}，策略集合为{Se1t，Se2t，…，Se（N）t}。 若在博弈过程中，某时刻t 的策略集合满足式（3），则博弈过程能够达到均衡状态。

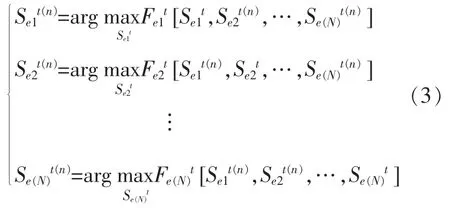
式中：{Se1t，Se2t，…，Se（N）t}是各分区的市场参与价格，为待优化的决策变量。

（2）约束条件

①各分区调节功率 之和与光伏出力误差ΔEe－pht应保持平衡，满足式（4）：

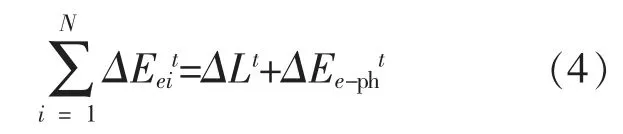
式中：ΔLt为负荷预测误差引起的调峰需求；ΔEe－pht为光伏预测误差导致的调峰需求。

②各分区的输出功率Peit+ΔEeit在各区的输出功率上、下限内，满足式（5）：

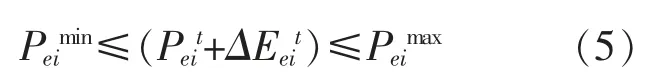
式中：Peit为第i 个分区当前的有功出力；Peimax，Peimin分别为第i 个分区的输出功率上、下限。

③各分区的调节功率ΔEeit在各区的调节能力上、下限内，满足式（6）：

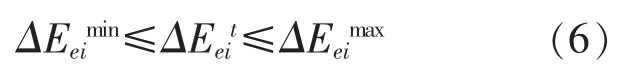
式中：ΔEeimax，ΔEeimin分别为第i 个分区调节能力的上、下限。

（3）基于逆向归纳法的模型求解

根据式（3）可知，文中建立的非合作博弈的解位于空间RN+1，且为非线性方程，求解难度较大。由于采用传统纳什均衡求解方法很难对其求解，为此本文提出基于逆向归纳的求解方法， 将其转为N 个独立方程求解的问题，有效地降低求解维数。基于逆向归纳的求解方法的基本思路：先逆序推导均衡态， 然后依次求出各参与决策者的策略集合（交换价格）。

由于各分区首先满足式（4）所示的调节任务，因此， 各分区首先对调节功率ΔEeit进行博弈，使得其收益最大化。 针对任意分区i， 其调节功率ΔEeit关于交换价格Seit的表达式为

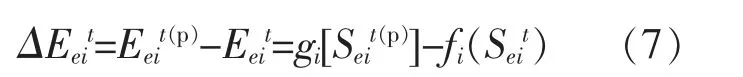
式 中：Eeit（p）为 第i 个 分 区的计划 功 率；Seit（p）为 第i个分区的计划电价；gi（·）为计划功率与计划电价函数关系式，可通过拟合得到。

在计划功率与预测功率误差允许范围内，可认为Seit（p）≈Seit，式（7）可简写为

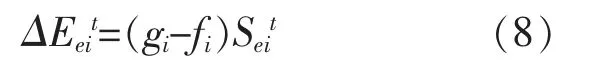
则

根据式（1）可得：

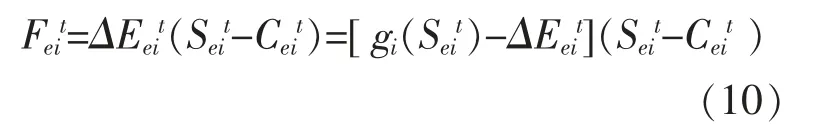
分区i 对其调节功率进行博弈，使其利益Feit最大，故博弈调节功率满足式（11）：

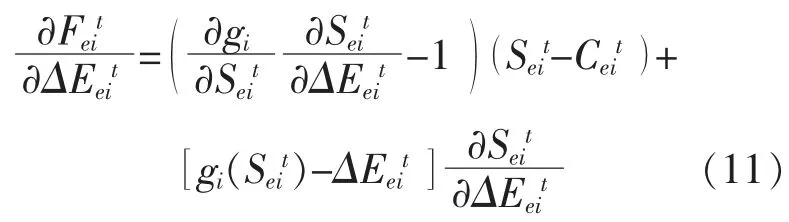
将式（10）代入式（11），可得：

由式（6）和式（7）可知，式（12）各分区的调节功率ΔEeit解应在式（13）的范围内取值。

对式（12）的解讨论如下。

①ΔEeit在可行域有解时， 表明各分区调节非合作博弈过程可以达到均衡状态。 为了使各分区调节功率满足式（4）的约束条件，将式（12）得到的调节功率按比例增减， 得到最后的均衡调节功率ΔEeit（n）。 最后根据式（9）可反推出其各分区均衡电价Seit（n）。

②ΔEeit在可行域无解时， 表明各分区调节非合作博弈过程无法达到均衡状态，此时，将越限分区i 的调节功率取式（13）的限值，即：

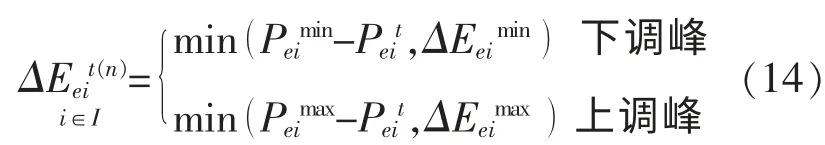
式中：I 为越限分区编号构成的集合。

根据式（4）和式（14）可得剩余的调峰功率：

该部分电量由未越限的分区i∈∃I 承担。 由于该部分分区的调节功率有解，只须将式（12）得到的调节功率（i∈∃I ）按比例增减，使最后的调节功率之和等于式（15） 所示的剩余调节功率即可。 最后根据式（9）可反推出其各分区电价Seit（n）。

3 基于合作博弈的上层调节曲线修正模型

（1）模型建立

合作博弈的核心： 将各分区决策者看作一个整体，采取合适的策略使得整体的利益最大，同时保证各决策者的利益平衡， 合作博弈决策须要在非合作博弈决策的基础上进行。从社会效益角度，希望各调节电源的综合效益达到最大。 将各调节电源看成一个联盟，联盟的收益函数集合为{F∑t}，联盟策略集合为{S∑t}。 博弈模型如下：

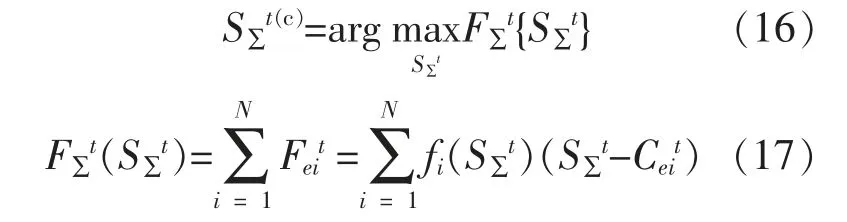
在式（17）中，各参与市场调节的分区地位等同。实际运行表明，部分分区会因为某些因素而出现违约现象，因此要对违约较大的分区进行惩罚，使其参与市场调节的份额较少。

设置权重系数为

式中：λei为考核期内分区代理的违约率。

式（17）可改写为

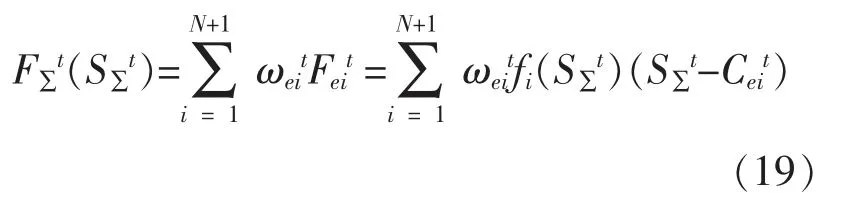
（2）模型求解

为了使联盟的收益最大， 联盟以交换价格进行博弈，须满足：

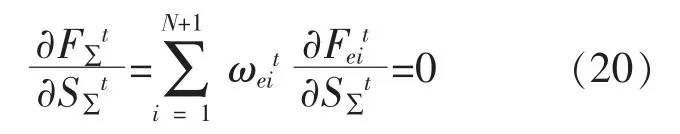
将式（19）代入式（20）可得：

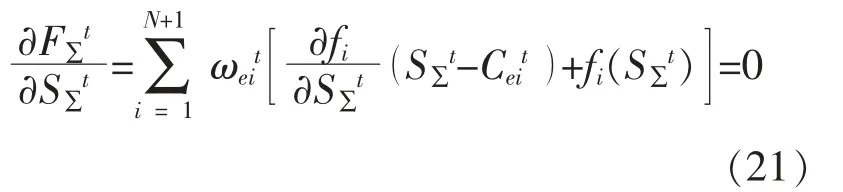
式（21）的解S∑t（c）即为联盟交易的均衡价格，联盟的均衡调节功率和收益分别为

首先，以非合作博弈结果为参考值，进行内部收益分配，计算各决策者对联合系统的贡献：

然后，根据式（24）按照贡献大小来分配收益。

上述合作博弈得到的调节曲线和收益以非合作博弈结果为基准， 考虑了各分区的意愿调节曲线，具有更高的可执行性。将得到的结果返回各分区进行校验， 若修正后的曲线在各分区调节能力范围内，则执行；否则，超过限值的分区取限值，剩余量由其他分区按照式（24）继续分担。

须要说明的是， 合作博弈在非合作博弈结果基础上进行， 只有当各决策者合作形成的联合系统收益大于非合作时的各决策者收益总和时，才有采用合作博弈修正调节曲线的必要。 调节曲线修正的条件为

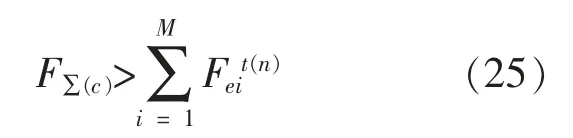
4 算例分析

4.1 算例简介

青海某地电网含有的光伏比例较高， 具有较大波动性， 需要附近梯水电站等调节电源参与联合调峰。 为了方便调节，设该电网有3 个代理，即分区代理A、分区代理B、分区代理C。 各代理下的调节电源终端调节特性如表1 所示。

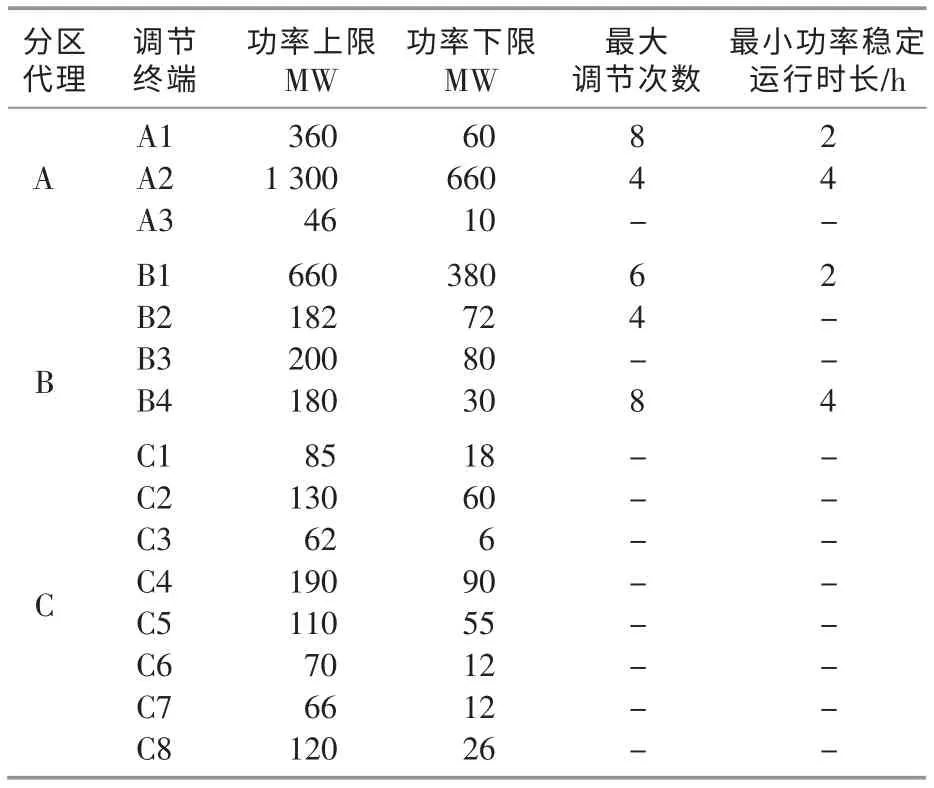
表1 各分区代理下负荷终端特性Table 1 Load terminal characteristics table for each partition agent

4.2 双层博弈调度经济性对比分析

为了对比分析本文所提出双层博弈方法的经济优越性，构建两个仿真方案：方案1 以联合系统收益最大为目标进行联合调度；方案2 按照本文提出的双层博弈调度方法进行联合调度。

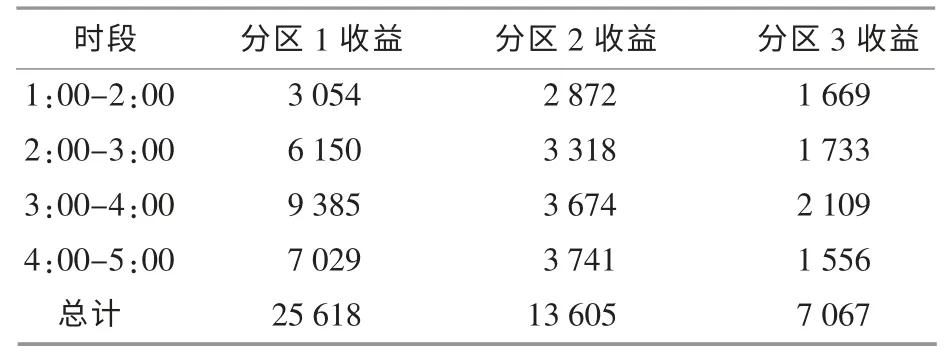
表2 方案1 联合调度经济性分析Table 2 Economic analysis of scheme 1 元

采用非合作博弈时，计算得到3 个分区的收益（表3）；采用合作博弈时，先根据式（23）计算3 个分区对联合系统的贡献，再分配内部收益（表3）。

表3 方案2 联合调度经济性分析Table 3 Economic analysis of scheme 2 元

从表2 和表3 可知， 与其他联合调峰方法相比， 本文所提出的双层博弈方法的非合作博弈调度和合作博弈调峰的总经济收益均有所提高； 并且采用合作博弈时各分区代理的经济收益会更好。

计算各分区代理的收入均匀度如表4 所示。

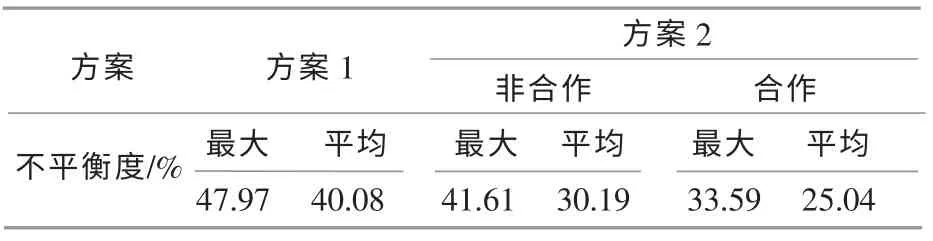
表4 收益均匀度情况Table 4 Income uniformity statement

由表4 可知，采用方案1 方法进行调度时，无法保证内部收益的相对均匀性， 内部收益相差较大，该方案虽然在技术上可行，但在经济上较难实施；本文所提的非合作博弈及合作博弈调度方法，可将内部收益不均衡度分别降低9.89%和15.04%，可保证内部的相对公平，因此在经济上也具有较大的可行性。

4.3 双层博弈调度违约率对比分析

为了对比分析本文所提出的双层博弈方法违约率情况，同样以方案1、方案2 为例进行分析。

按照方案1 和方案2 得到的各分区的调节电量示于图2。

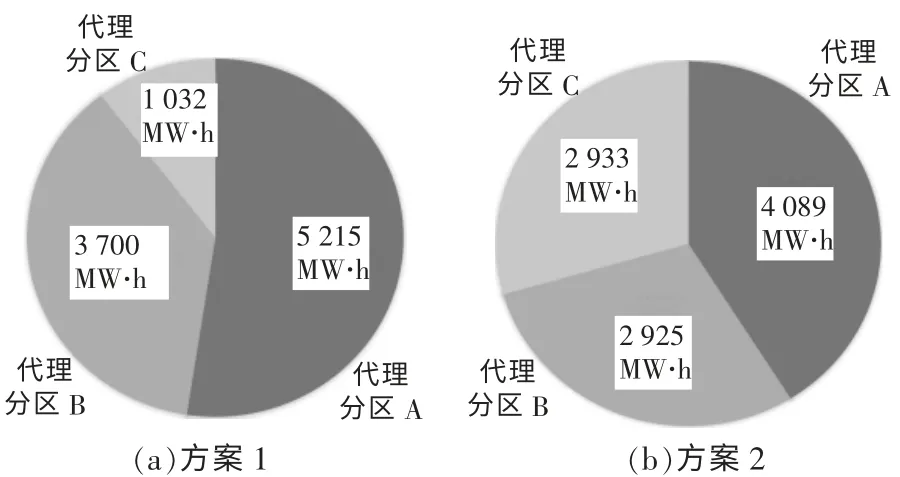
图2 各分区代理调节电量Fig.2 Electricity regulation by each partition agent

如图2（a）所示，采用方案1 进行调度时，会将大量的调节量分配给分区代理A 和分区代理B。 结合表2 分析可知，这是由于分配至该两个分区代理会使得效益最大所致， 可能引起违约现象的发生。 调节后的电量分配如图2（b）所示。 采用本文所提调度方法，增加了各分区代理确认环节，各分区代理更加了解所代理调节实体的调节能力，有效降低违约率。

两个方案的违约情况如表5 所示。

表5 违约情况Table 5 Breach of contract

由表5 可知，方案1 的违约率较高，主要因为分区代理1 和分区代理2 的调节限制较多， 而调度中心无法实时掌握其调峰能力， 将大量调节电量分配给分区代理1 和分区代理2。 因此，须要减少分区1 和分区2 的调节电量， 增加分区3 的调节电量。

5 结论

针对目前光伏出力波动调解过程中出现的违约率较高和内部收益不均的问题， 提出了基于双层博弈的水、光、储综合系统分区调峰方法。 该方法一方面可以通过价格博弈获得经济可行解，避免内部收益相差过大； 另一方面可以通过分区代理的确认环节，减少调节违约率的发生，降低系统调节压力。

以实际电网为例进行分析表明， 本文所提出的调峰方法具有如下优势。

①采用双层博弈调峰方法分配调峰任务时，虽然会在一定程度上降低系统整体收益， 但会使系统内部收益相对均衡，便于执行。

②对于水、光、储联合调峰系统，采用合作博弈时各决策者的收益均比非合作博弈有不同程度增加，且系统内部各决策者的内部收益更加平衡。

③增加分区代理层和代理调节曲线确认环节，可以有效地降低各分区调节违约率，降低系统调节压力。