导流涵道安装角度对垂直轴水轮机性能影响研究

刘清照，陈 兵

（1.中国船舶重工集团公司 第七一三研究所， 河南 郑州 450000； 2.大连理工大学 海洋科学技术学院， 辽宁盘锦 124221）

0 引言

20 世纪50 年代，为了提高风力发电效率，有学者提出增加风力导流涵道，其概念又被称为扩散器[1]。 1978-1983 年，Gilbert B L 通过研究发现，相比于无扩散器，将扩散器运用于风机后，风机效率可提高90%[2]，[3]。 随着研究的进一步深入，近年来， 研究者将导流涵道运用到潮流能水轮机上，并对导流涵道内部形状进行优化。 大量研究表明，安装导流涵道可以有效提高潮流能垂直轴水轮机的能源利用率且大幅度降低其转动波动。Ponta[4]通过实验测试了不同导流罩的水动力特性。Malipeddi A R[5]研究了多种情况下导流涵道的外形参数值对Darrieus 水轮机水动性能的影响，指出导流涵道的外形变化可将水轮机的发电效率从0.4 增加到最大的0.63。 张亮[6]对6 种不同形式的导流涵道的增速性能进行了数值和实验研究。 陈晗[7]对安装有导流涵道的弹簧控角水轮机进行实验研究，发现安装导流涵道的水轮机性能比单独水轮机性能更好。

导流涵道的利用虽然提高了水轮机的能源利用率，同时也带来了一些问题。 首先是转子上增加导流涵道后， 涵道内的流场变得更加复杂，叶片和导流涵道的受力情况有待进一步研究。 其次，目前的实验和数值模拟，主要针对来流速度方向与导流涵道安装方向一致进行研究， 当来流方向变化时， 叶轮和导流涵道的水力学性能并未有过详细的研究。

本文主要针对导流涵道安装角度α 为0～10°时（角度过大没有太大研究价值），利用二维数值模拟研究的方法， 研究带导流涵道垂直轴水轮机叶片、转子以及导流涵道的受力情况，并对导流涵道对垂直轴水轮机工作效率以及扭矩的影响进行分析，为以后增速装置的安装设计提供支持。

1 导流涵道及水轮机的模型参数

本文主要研究H-Darrieus 型潮流能垂直轴水轮机， 模型中不计算转轴与叶片中间的连接臂对水轮机的影响，其设计参数如表1 所示。

表1 垂直轴水轮机的设计参数Table 1 Parameters of vertical turbine

程帅兵[8]提出了一种新型的导流涵道，本文采用相同的导流涵道外形，导流涵道的α 用导流涵道安装方向与来流方向的夹角表示，计算中来流速度不变，通过改变导流涵道安装方向从而改变α，水轮机转子模型如图1 所示。

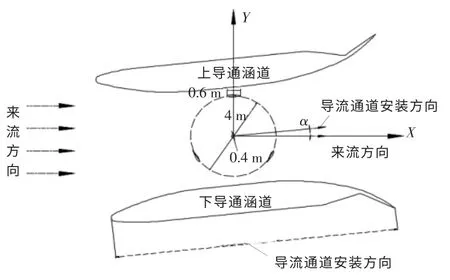
图1 水轮机转子模型Fig.1 Model of the rotor

2 数值研究模型

2.1 叶片和水轮机受力

水轮机叶片在转动过程中受到来流作用产生的升力L、 阻力Dr和对转轴轴心O 的力矩Mo是分析水轮机叶片和转子受力情况的基础。 图2 为单个叶片的相对速度和受力图，图中：α 为叶片几何攻角；θ 为叶片方位角；φ 为叶片偏角；ω 为旋转角的角速度；R 为转子半径。

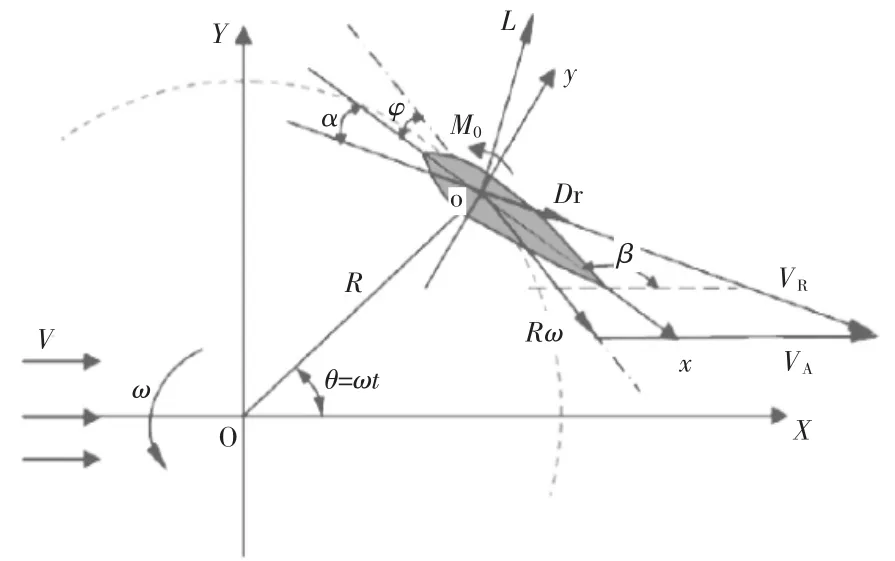
图2 单个叶片的相对速度和受力图Fig.2 Relative velocities and forces on single blade

定义单个叶片的弦向力Fx和法向力Fy为

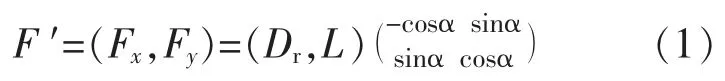
水轮机转子受到单个叶片的切向力Ft和径向力Fn为

对于固定偏角的水轮机：

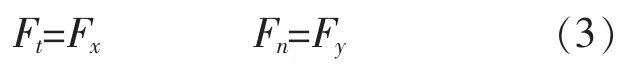
单个叶片对转子的推向力tx和侧向力ty为

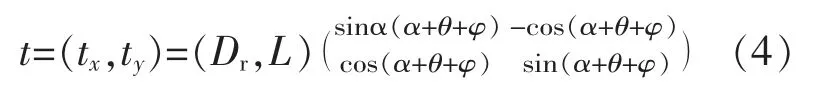
故单个叶片的受力对水轮机转轴轴心的力矩为

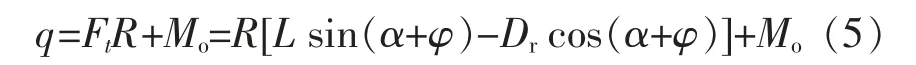
所有叶片受到的平均推力Tx、 平均侧向力Ty、平均转矩Q 以及功率P 为

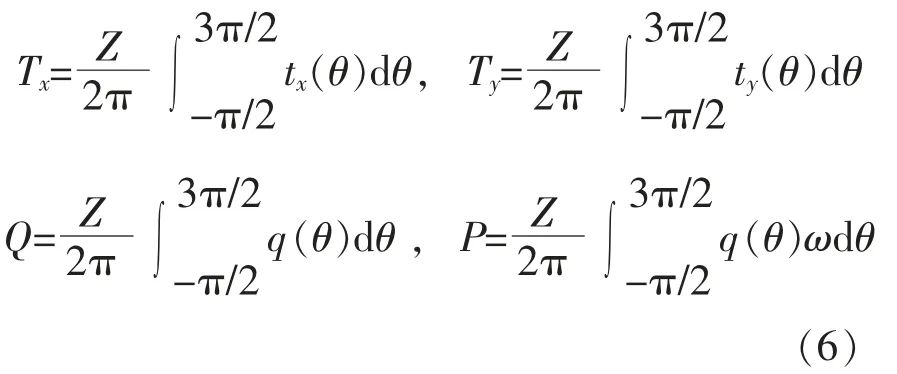
水轮机转子的转速大小由自身的转动惯量J、作用在叶片上的水动力力矩Mω、摩擦阻力力矩MR、输出端的负载力矩Ml决定。 控制方程以及负载力矩为[9]

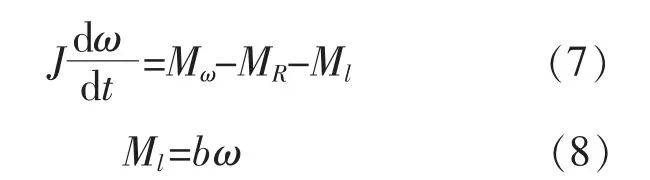
式中：b 为负载阻尼系数。

将垂直轴水轮机的转子的输出转矩系数（CQ）和平均能量利用率系数（CP）表示成无量纲形式为

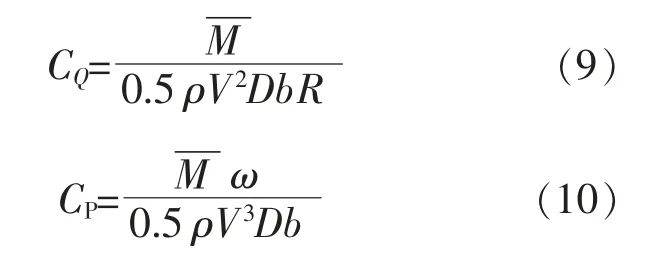
2.2 数值模拟计算

本文采用ANSYS Fluent 14.0 进行数值模拟计算，满足流体运动的N-S 方程[10]，在不考虑三维模型效应以及自由液面对水轮机影响的前提下，采用非定常隐式求解，湍流模型选用K-ω SST 湍流模型，速度和压力耦合采用SIMPLE 算法，时间步长设定为0.005 s。

根据表1 中水轮机的基本参数， 建立了适当的计算域。整个计算域分为外部流体域区、导流涵道旋转区以及转子旋转区。 整体计算区域如图3所示。

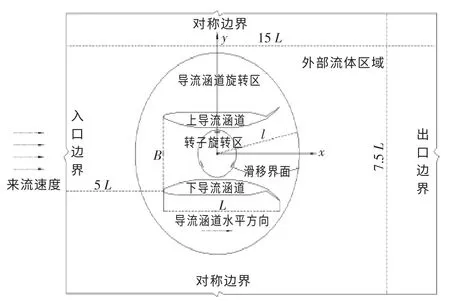
图3 整体计算区域Fig.3 Total computational domain

流体域长度为15 L（L 为导流涵道的水平长度），宽度为7.5 L。 流体域入口设置为速度入口（速度大小为1.5 m/s），出口设置为压力出口，上下边界设置为对称边界，导流涵道设置为固壁边界，旋转部分采用滑移壁面边界。为减小误差，提高计算精度，采用结构化网格划分，并对水轮机转子以及叶片周围网格进行加密处理并确保Y+=1， 经网格无关性验证， 最终网格数约为27万（图4）。

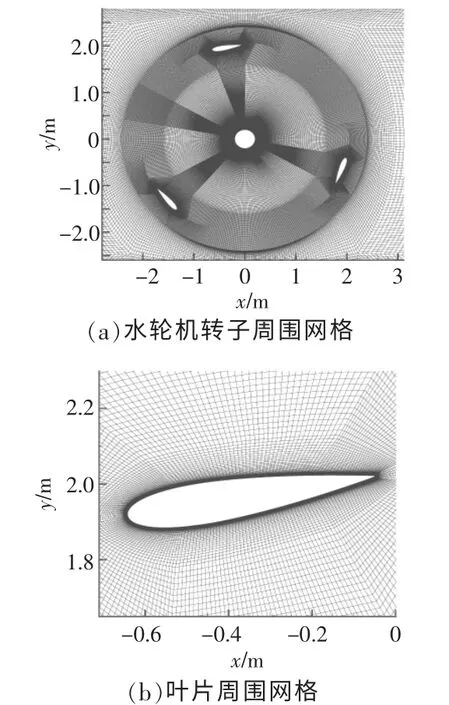
图4 叶片网格系统Fig.4 Grid system of rotation blades

3 结果与分析

3.1 带导流涵道水轮机的能源利用率

为避免流场中初速忽然增大而造成的计算误差，计算时，无穷远来流采用初速从零逐渐增大到1.5 m/s，取水轮机转子稳定后数据进行分析。尖速比λ（TSR）是垂直轴水轮机最重要的设计参数，改变水轮机的负载阻尼系数b， 可以得到水轮机的能源利用率系数随λ 的变化曲线（图5）。 由图5 可知， 水轮机的能源利用率系数随着λ 的增大先增大后减小，且b 为2 200 时，此时λ 为1.89，水轮机能源利用率系数Cp 达到最大值0.658。 故本文讨论当b 为2 200，α 为0，2，4，6，8，10 °时，导流涵道不同安装角度对垂直轴水轮机的水动力学性能的影响。

图5 α=0°时Cp 的变化曲线Fig.5 Variation curve of power coefficient at α=0 °

图6～8 分别为不同α 时的λ，Cp、输出转矩Ct的变化曲线。 由图6～8 可知：λ，Cp以及Ct均随着α 的增加而减小； 当α 为0°与10°时，Cp最大减少13.6%，且α 从0°到2°时，减小幅度最大，说明当α 为0°时， 进入导流涵道的流体将增加，故此时λ 最大，潮流能水轮机的性能最好，Cp最大。

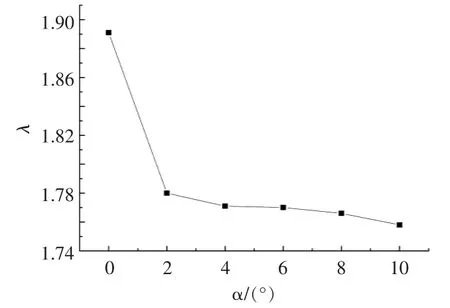
图6 α 不同时λ 的变化曲线Fig.6 Variation curve of TSR in different angle

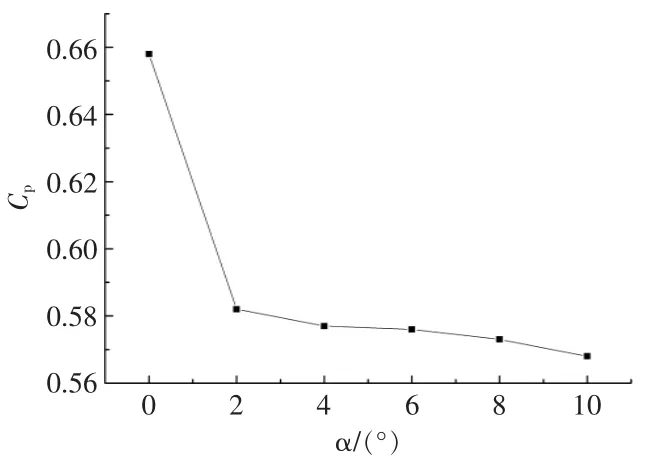
图7 α 不同时Cp 的变化曲线Fig.7 Variation curve of power coefficient in different angle

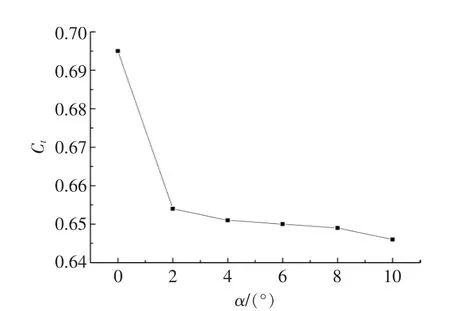
图8 α 不同时输出转矩系数的变化曲线Fig.8 Variation curve of output torques coefficient in different angle

在实际工程中，潮流来流方向时刻在改变，且导流涵道的安装方向与来流方向不可能绝对相同， 所以研究导流涵道的安装角度对垂直轴水轮机有着重要的意义。

3.2 水轮机叶片水动力分析

为方便研究和分析，各参数采用真实值表示，不采用无量纲处理。 水轮机转子的受力情况与水轮机叶片受力有着直接的关系，α 不同时，单个叶片所受推力、侧力和平均力的变化曲线如图9～11所示。

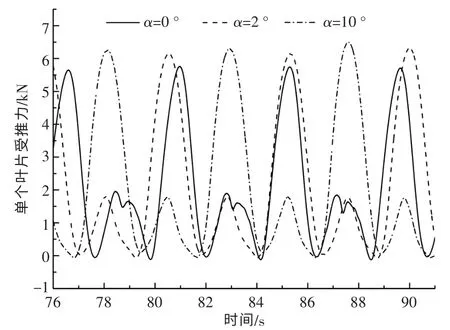
图9 单个叶片所受瞬时平均推力Fig.9 Instantaneous average thrust on a single blade

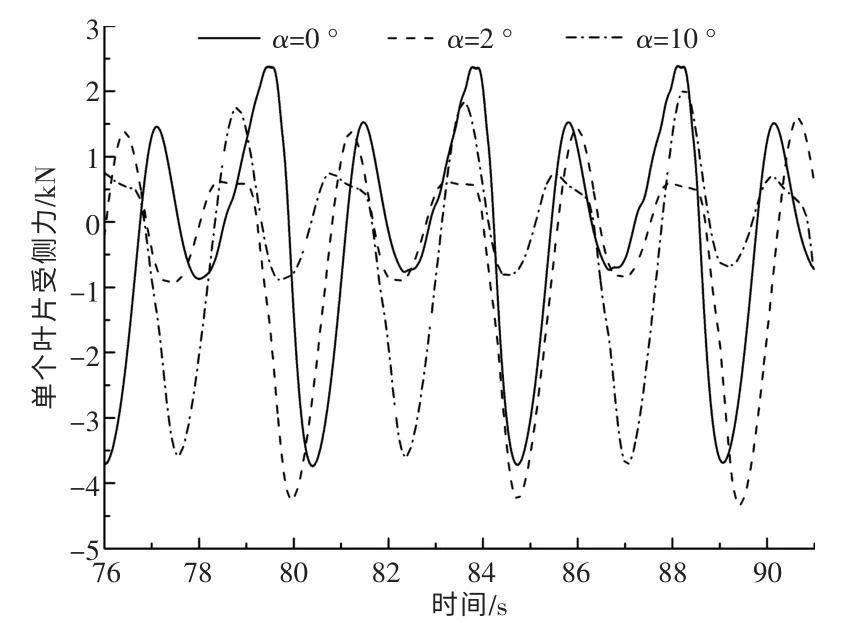
图10 单个叶片所受瞬时平均侧力Fig.10 Instantaneous average lateral force on a single blade

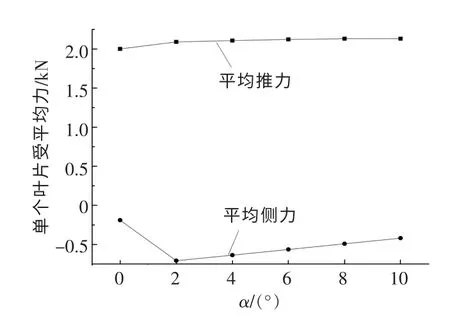
图11 α 不同时单个叶片所受平均力Fig.11 A single blade receives an average force at different angle

由图9 可知： 在转子旋转的上半区域，α 越大，单个叶片的瞬时受力越大；在转子旋转的下半区，当α 为0°时有两个波峰，而当α 为2°和10°时，只有一个波峰，且数值大小基本相同，故单个叶片所受平均推力随着α 的增加而增加， 且当α从0°增加到2°时，增加幅度最大，符合图11 中单个叶片所受平均推力的变化趋势。 由图10 可知，当α 为2°时，叶片所受瞬时负方向侧力值最大，随着α 的增大，叶片所受瞬时负方向侧力的绝对值在变小，符合图11 中当α 从0°增加到2°时，侧力绝对值忽然增大，而后绝对值缓慢减小的变化趋势。 出现这种现象是由于转子两侧流体速度发生变化，转子在上下旋转半区受力发生改变。

图12 为α 不同时单个叶片所受瞬时转矩的变化曲线。 由图12 可知，当α 为0°时，转子旋转的下半周期较其他角度有着明显的增加， 且增加时间较长，故单个叶片对转子的平均力矩最大。

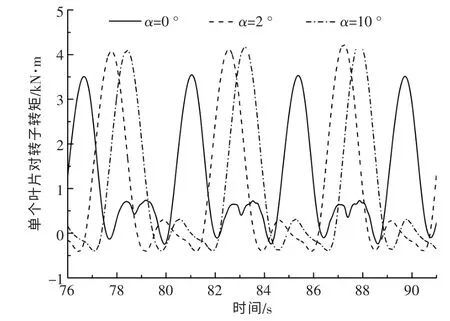
图12 α 不同时单个叶片所受瞬时转矩Fig.12 Instantaneous moment of a single blade at different angle

图13 为α 不同时单个叶片所受平均转矩的变化曲线。 由图13 可知，随着α 的增大，单个叶片所受的平均转矩逐渐减小， 由于输出转矩主要由叶片提供， 故输出转矩的变化规律与其有相同的变化趋势。

图13 不同α 单个叶片受平均转矩Fig.13 The average torque of a single blade at different angle

从上述结果可知，当α 发生改变时，对叶片所受的侧力的方向有较大的影响， 在实际工程应用中应对叶片侧向受力情况更加重视。

3.3 水轮机导流涵道水动力分析

当导流涵道安装方向发生变化时，上、下导流涵道的受力情况将发生很大的变化。

图14，15 分别为α 不同时，导流涵道的受力和受转矩变化曲线。

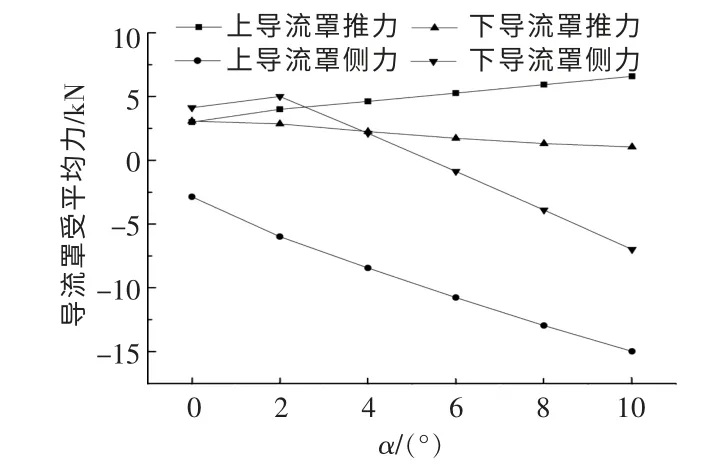
图14 α 不同时导流涵道的受力情况Fig.14 Force on channel at different angle

图15 α 不同时导流涵道的受转矩情况Fig.15 Torque on channel at different angle

由图14 可知：随着α 的增大，上导流涵道所受平均推力在逐渐增大， 受平均侧力绝对值也在逐渐增大， 下导流涵道受到的平均推力在逐渐减小；但当α 为6°时，下导流罩受到平均侧力值由正向变为负向，且所受负向力值在增大。 由图15可知：随着α 的增大，上、下导流涵道受平均转矩在逐渐增大， 故α 对上下导流涵道的影响非常大，α 越大， 上导流涵道受到的力和力矩越大，对导流涵道的强度要求越高。

α 为0°和10°时，上、下导流涵道瞬时受力对比分析曲线分别如图16，17 所示。

图16 α 为0°时上下导流涵道瞬时受力Fig.16 Instantaneous force on channel at α=0°

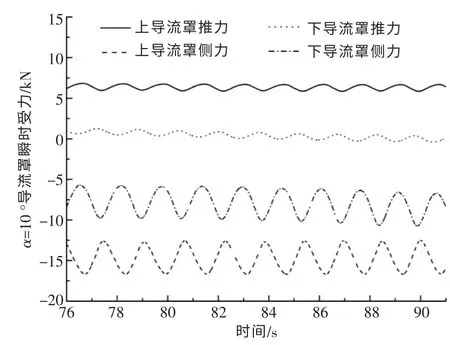
图17 α 为10°时上下导流涵道瞬时受力Fig.17 Instantaneous force on channel at α=10°

由图16 可知，当α 为0°时，上、下导流涵道所受瞬时推力方向相同， 且周期和大小也基本相同， 所受侧力的周期和值大小基本相同， 方向相反，侧力的波动幅度明显大于推力的波动幅度。由图17 可知：上导流涵道所受推力值增大，且所受侧力方向发生改变，侧力值明显增加；下导流涵道所受推力值变小， 所受侧力值方向不变但测力值明显增大。 说明上、下导流涵道在α 变大时，工作环境变差，上、下导流涵道受到的侧力值明显增加。

3.4 水轮机速度场分布情况分析

通过前文的结果数据，得到水轮机转子在稳态工作时的水轮机叶片和导流涵道的受力情况。 图18 为α 为0，2，6，10°时的速度场分布图。

图18 α 不同时的速度场分布Fig.18 Distribution of velocity flow field at different angle

由图18（a）可知，水轮子转子的速度呈对称分布，上、下导流涵道受到的力和力矩数值相同。由图18（b），（c），（d）可知：转子尾部速度场发生明显变化， 导流涵道内流体接近下导流涵道处的速度明显高于上导流涵道，且α 越大，这种现象越明显；对于导流涵道外部流体，随着α 的增大，接近下导流涵道前部的流体速度在逐渐增大， 接近上导流涵道中部的流体速度在逐渐减小； 同一流场中，速度越大的位置压力越小，故下导流涵道受到的侧力方向会由正到负， 上导流涵道受到导流涵道内外的压力差在不断增大， 上导流涵道所受到的力和力矩均随着夹角的增加而增加， 导流涵道工作环境变差。

4 结论

本文通过改变导流涵道α（0～10°），对带导流涵道的垂直轴水轮机水动力学性能进行了分析，并通过速度场云图对水轮机各部分进行受力情况的分析，得到以下结论。

①当来流方向与导流涵道安装方向相同 （即安装角α=0°）时，垂直轴水轮机的输出转矩和能源利用率系数最大， 能源利用率系数最大值可达0.658。

②当来流方向与导流涵道安装方向不同时，随着α 的增大， 带导流涵道水轮机的尖速比、输出转矩、能源利用率系数逐渐减小，且能源利用率系数最大减小为13.6%， 故建议安装角度尽量减小，最好不大于10°。

③当来流方向与导流涵道安装方向不同时，随着α 的增大，水轮机叶片受到的平均切力会逐渐增加，平均推力和平均扭矩会逐渐减小，上导流涵道的水动力情况更加恶劣， 在实际工程应用中建议考虑α 对导流涵道的影响。

通过导流涵道α 对垂直轴水轮机水动力学影响分析， 建议在实际工程中将导流涵道设计为安装方向可自动调节， 以提高垂直轴水轮机的性能。