基于Hotbooting Q 算法的多微网能量交易博弈模型

李 聪， 余加喜， 姜 文， 吴清玉， 宋丽珠， 莫若慧， 吴 锋

（南网海南电网电力调度控制中心， 海南 海口 570100）

0 引言

随着分布式电源接入电网比例的不断提高，其出力的随机性和间歇性对电力系统的安全稳定运行构成了威胁。 微网（MG）通过先进的通信、计量和协调控制技术，将分布式电源、储能系统等多种分布式能源聚合，通过协调内部各机组出力，极大地减小了分布式电源单独并网对公网造成的冲击，缓和了风光等可再生能源的波动性，实现了资源的优化配置和协调管理，提高了市场竞争力[1]～[3]。

MG 参与电力市场交易可带来诸多益处，其交易行为不可避免地会受到其余MG 以及上级电网的影响，博弈论是目前有效处理MG 电能交易的方法。文献[4]考虑了多MG 参与配电市场竞标，并基于完全信息博弈求解不同策略下的MG投标电量与投标电价，对MG 参与配电市场以及零售市场的交易机制进行了验证。文献[5]构建了MG 间博弈交易模型以及MG 内部博弈交易模型。 然而，对于竞争的电力市场，MG 间往往是竞争关系而非合作关系，因此，非合作博弈模型在MG 能量交易中的使用更为合理。 文献[6]提出了基于贡献机制的电能交易策略， 当负荷需求高峰、MG 内部供电不足时，贡献值越高的MG 可优先获得上级电网的电量供应。文献[7]从非合作博弈理论出发，设计了MG 剩余电量参与电力市场的价格竞争机制，并从各MG 电能不足的概率角度，证明了所建立的非合作博弈模型存在唯一纳什均衡点。

上述文献在对博弈模型的求解上多采用的是常规的迭代求解，对不确定性因素的处理多采用的是场景法或随机规划法，且决策往往是在日前进行，难以做到实时分析与在线决策。 强化深度学习法能够依托MG 的大量经典数据， 根据实际的调度要求与优化目标，给出对应的控制方案以及优化策略，实现对大数据的处理，达到实时在线决策的目的。 文献[8]，[9]基于强化深度学习法对MG 内部复合储能调度进行优化， 实现了变量的实时在线决策控制，并且在不同时刻、天气、季节等场景下均能有效处理。 文献[10]，[11]构建了一个基于强化深度学习算法优化的MG 平准化电能成本的长短期电能管理方案，从规划和运行的角度将深度学习算法融入到MG 的实时运行与调度中。

本文首先建立了多MG 电能交易博弈模型，并将MG 的电能博弈定性描述为马尔科夫过程。然后建立了基于强化深度学习的MG 电能交易模型， 通过Hotbooting 技术获得相似场景下的Q 学习算法的Q 值表和V 值表，大大减少了Q 学习算法的学习步长，提高了算法的收敛性，且具有良好的学习效果。

1 MG 间电能交易博弈机制设定

本文考虑的MG 由风光等新能源机组、 电储能系统、负载端需求响应组成，各部分模型建模如下。

1.1 光伏发电模型

根据太阳辐射强度，光伏阵列输出功率为

式中：ηct为光伏阵列能量转换效率；SCA为光伏阵列面积；Gt为某地t 时间段的实际太阳辐射强度。

1.2 风机发电模型

DG 的出力与环境风速有着直接关系， 一般采用二参数的威布尔分布描述风速分布模型，风电输出功率表达式为

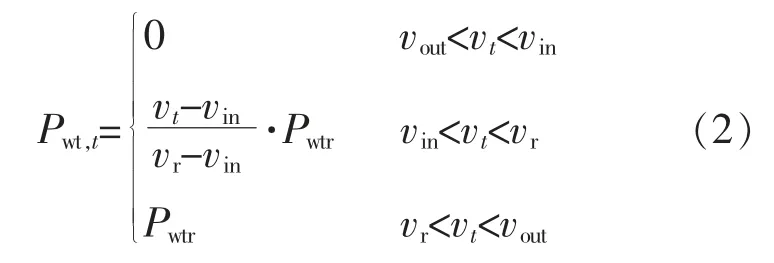
式中：vt，Pwt，t分别为t 时刻环境风速、 风电输出功率；Pwtr为风电额定输出功率；vin，vr，vout分别为 切入风速、额定风速、切出风速。

根据式（1）和（2），k 时刻的估计误差为

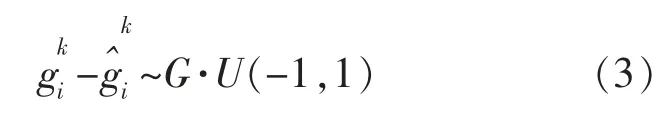
1.3 多微网电能交易博弈模型

考虑到风光电出力的不确定性，MG 须根据实际的风电出力向上级电网进行购电以满足辖区内负荷需求。 为减少MG 与上级电网间的电量交易，本文设计了MG 间的电量交易机制，如图1 所示。 当MGi 电量不足时，首先与MG 进行信息交流，假设此时MGj 为电量盈余微网，则MGj 可以与MGi 进行电能交易。 此外，同一个时刻，往往会有多个MG 处于电量紧缺状态， 同时也会有多个MG 处于电量盈余状态， 于是MG 间的电量交易构成博弈模型，在不考虑MG 间联盟的前提下，可认为这是一个非合作博弈模型， 每个MG 以自身利益最大化参与电能交易。

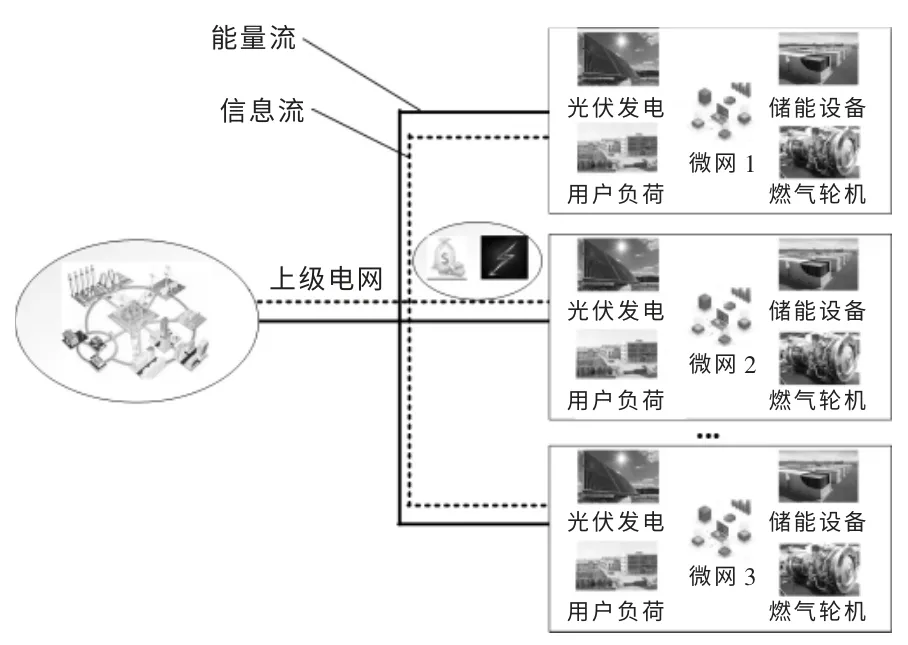
图1 多MG 电能交易场景示意图Fig.1 Schematic diagram of multi microgrid electric energy trading scenario

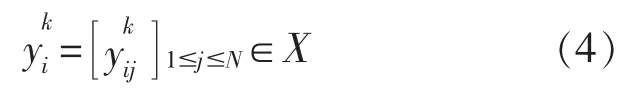
为充分消纳风电等新能源出力， 减轻MG 对于上级电网的依赖， 应尽可能地减少MG 与上级电网的交易电量， 从而减少煤炭等的使用以及污染气体的排放。 故应当让系统优先考虑MG 间的电能交易，MG 间的具体交易模型图如图2 所示。

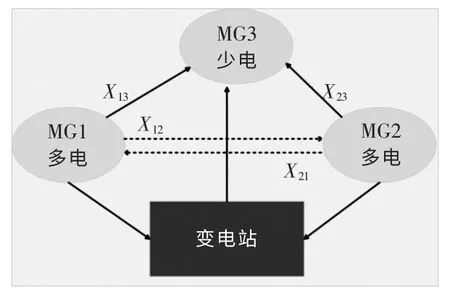
图2 多MG 电能交易模型图Fig.2 Multi microgrid power trading model

在MG 间交易优先的情况下， 交易规则及步骤如下：

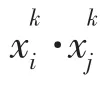
②MG 间优先进行交易， 当交易电量无法满足时，再考虑从变电站进行购售电。

基于以上原则，双方的交易规则可表示为

上述公式表明，MGi 与MGj 之间只存在一次交易，电能交易过程是电量守恒的，满足对称性。由此可推导MGi 与变电站之间的实际电量交易yii为

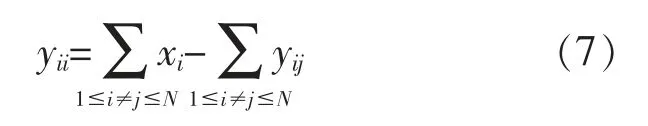
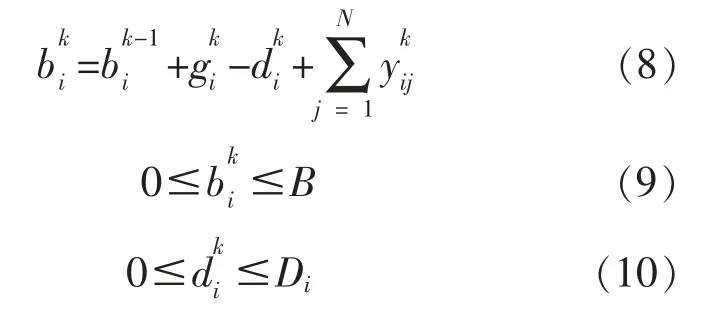
由上述公式可知， 电量的变化必然导致MG的增益发生改变。 为刻画电量的增加对MG 收益带来的影响，设置增益函数并对其具体表达式进行研究。 MG 的增益主要取决于储能设备储电量的增加，故首先增益函数G（b）为单调增函数，其次，考虑到其余MG 的缺电量不可能无限增大，故当储电量达到一定值后，多余的电量只能以较低的价格出售给变电站。 因此随着电量的变化，G（b）的增长速度应逐渐减小。 此处以对数函数刻画增量函数[12]：

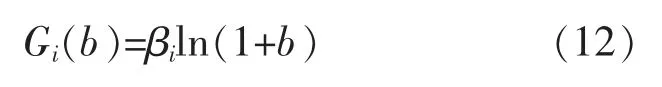
式中：βi为大于0 的系数， 反映MGi 对内部负荷的供电能力。

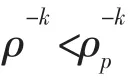
系统的效益函数为

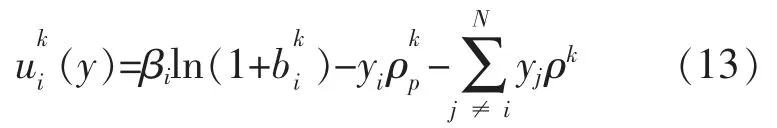
进而推导出MGi 的效益函数为

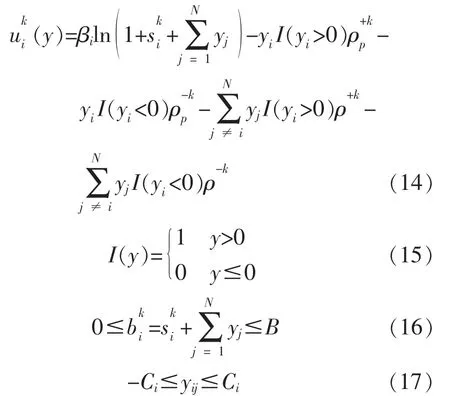
2 基于Hotbooting Q 学习的MG 电能交易

2.1 基于深度Q 学习算法的MG 电能交易

MG 与上级电网或者其余MG 进行电量交易，将会影响下一时刻电量的存储值以及其余MG 交易决策， 因此，MG 的电能交易博弈可以马尔克夫过程描述。 在动态博弈中，当其余MG 的电量水平以及MG 自身的负荷需求未知时，MG 可使用深度Q 学习算法获得满足自身利益的电量交易策略。

MGi 的瞬时效益函数为

MGi 根据自身的交易策略，不断地对Q 函数进行实时更新，具体计算式如下：

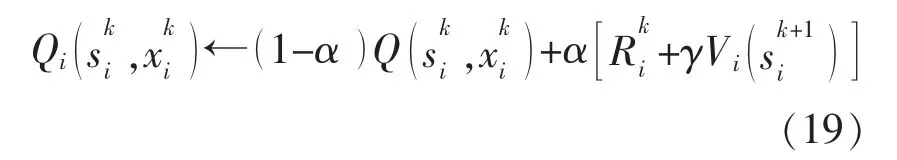
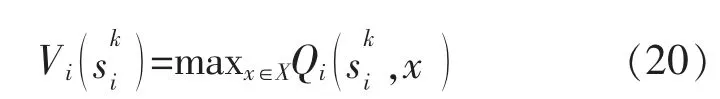
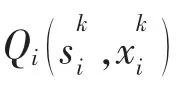
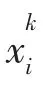
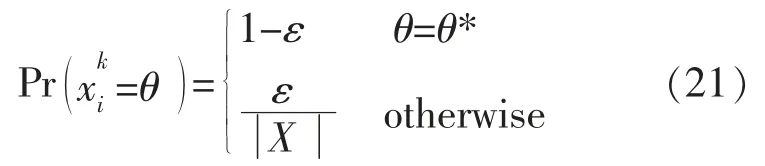
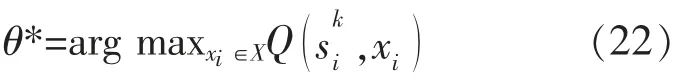
至此， 本文建立了基于深度Q 学习算法的MG 电能交易博弈模型。

2.2 Hotbooting 技术在深度Q 学习算法中的应用

深度Q 学习算法在初始化Q 值表时往往将其中所有元素简单的化为0， 每次在重复学习前将从0 开始进行大量的探索与训练， 极大地缩减了学习效率。 如果能够将Hotbooting 技术与深度Q 学习算法相结合， 则能大大缩短前期的训练时间，提高算法的收敛性。

根据以往电能交易的相似场景，在相似的环境下通过大规模的仿真实验获取训练数据，在此训练数据的基础上通过Hotbooting 技术对Q 值表和V 值表进行初始化处理， 用处理后的Q 值表和V 值表替代原来初始化的Q 值表和V 值表。

具体的模型求解步骤如下：

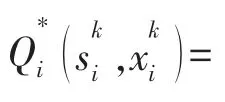
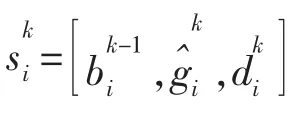
③通过数据筛选，得出合法的交易值；

⑤将交易策略及时汇报，并更新电量值，获取下一时段状态；

⑥使用Hotbooting 技术模拟交易， 获得模拟Q 值表、V 值表；

⑦深度Q 学习算法交易控制中心调整交易策略，获得最佳预期效益。

系统的求解流程图如图3 所示。

图3 基于Hotbooting Q 交易算法的求解流程图Fig.3 Solution flow chart based on Hotbooting Q transaction algorithm

3 算例分析

本文建立了基于Hotbooting Q 学习的MG 电能交易算法，并通过MATLAB 编程完成了对上述模型的仿真计算。 场景设定为智能电网下存在一个由变电站（PP）以及3 个MG 组成的博弈框架，研究四者之间的电能交易策略， 设定MG 用户为利益主导型， 即每次迭代MG 均以自身利益最大化作为优化目标。

3.1 实验数据及案例描述

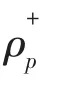
智能体采用贪婪算法以保证学习过程不陷入局部最优解，即有1-ε 的概率选择式（22）的策略，贪婪系数ε 取为0.8[10]，产生随机动作的概率为1-ε=0.2， 同时更新并继续计算新的Q值， 直至实验结束。 在强化学习中，α 取0.7，γ取0.8，设置学习步长为5 000 步，学习次数为500 次。

3.2 算法效率及有效性测试

为了对不同的结果进行对比， 本文设置了3种仿真案例，分别作如下描述：

Case1： 采用Hotbooting Q 交易算法对多MG电能交易博弈模型进行求解；

Case2：采用深度Q 学习算法对多MG 电能交易博弈模型进行求解；

Case3： 采用Greedy 策略对多MG 电能交易博弈模型进行求解。

图4 为3 种案例下的MG 电能交易后的平均效益变化情况。从图中可以看到：采用Hotbooting Q 交易算法和深度Q 学习算法时有一个明显的学习过程；而从收敛速度上看，相比深度Q 学习算法，采用Hotbooting Q交易算法要快很多，在学习步长进行到500 步左右即可完成收敛， 而深度Q学习算法要在3 500 步左右完成收敛。这主要得益于Hotbooting 技术在交易开始前便对相似场景下的数据进行了大量的模拟，因此后续的学习探索阶段的时间大大减少，可以较快掌握外界环境的交易规则以及交易规律。另外，如果交易过程单纯使用Greedy 算法，并不能从交易数据中获得经验，没有学习过程，且交易的效益也较差。可见，采用Hotbooting Q 交易算法对于提高整个算法的收敛性是有效的。

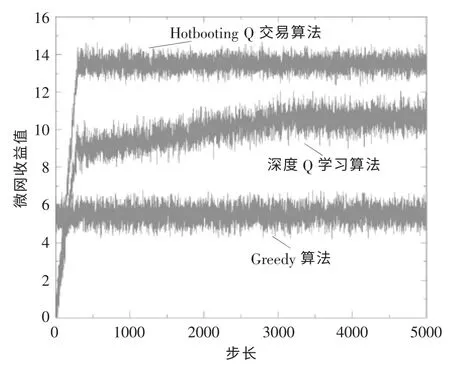
图4 不同算法的MG 电量效益Fig.4 Power efficiency of microgrid with different algorithms

从MG 收益的角度分析，采用Greedy 算法交易策略的收益很不理想，其收益值为5.8 左右；采用深度Q 学习算法的收益值为10.5 左右，与Greedy 算法相比， 收益值提高了44.76%； 采用Hotbooting Q 交易算法的收益值最终稳定在13左右，相较于深度Q 学习算法和Greedy 算法分别提高了15%和55.6%， 且收敛速度明显优于深度Q 学习算法。 因此，本文提出的Hotbooting Q 交易算法是行之有效的。

本文所提出的多MG 电能交易博弈模型的主要目的是为了减少MG 从上级电网的购电量，增加MG 间的交易电量， 提高MG 独立运行的安全性与稳定性。 图5 展示了在学习步长为5 000 步下的MG 从上级电网的购电量曲线。 与上述分析一致，在收敛速度上，Hotbooting Q 交易算法依然领先于深度Q 学习算法。 从削减MG 向上级电网购电量的角度来看， 采用Hotbooting Q 交易算法时，在步长为3 500 步（此时3 种算法均已收敛）时，MG 向上级电网的购电量为0.08，而深度Q 学习算法的结果为0.15 左右，Greedy 算法维持在0.42 左右。 可见，Hotbooting Q 交易算法不论在收敛速度上还是在最终的计算结果上， 均能取得很好的效果， 与深度Q 学习算法和Greedy 算法相比，MG 从上级电网的购电量分别较少了75%和60%，达到了预期的效果。

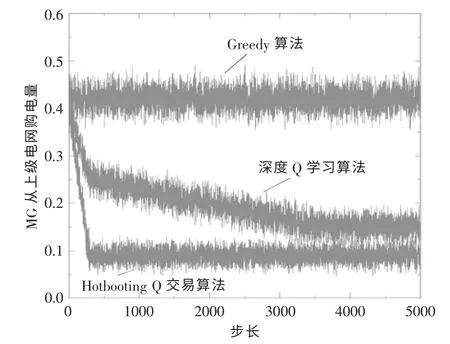
图5 MG 从上级电网购买电量曲线Fig.5 Micro grid purchases electricity curve from superior grid

本文将一天24 h 设置为0：00-6：00，7：00-12：00，13：00-18：00 和19：00-24：00 4 个时段，每个时段进行一次交易， 考虑到用户用电负荷的峰谷情况， 预设在1～6 h 所有MG 的电量储存值为0。 同时设置4 个参考算例，具体算例描述如下：

Case1：MG 间不进行交易；

Case2： 采用Greedy 算法对多MG 电能交易博弈模型进行求解；

Case3：采用深度Q 学习算法对多MG 电能交易博弈模型进行求解；

Case4： 采用Hotbooting Q 交易算法对多MG电能交易博弈模型进行求解。

图6 显示了在4 个交易时段下， 当3 种算法均收敛时，MG 从上级电网购电量的变化情况。

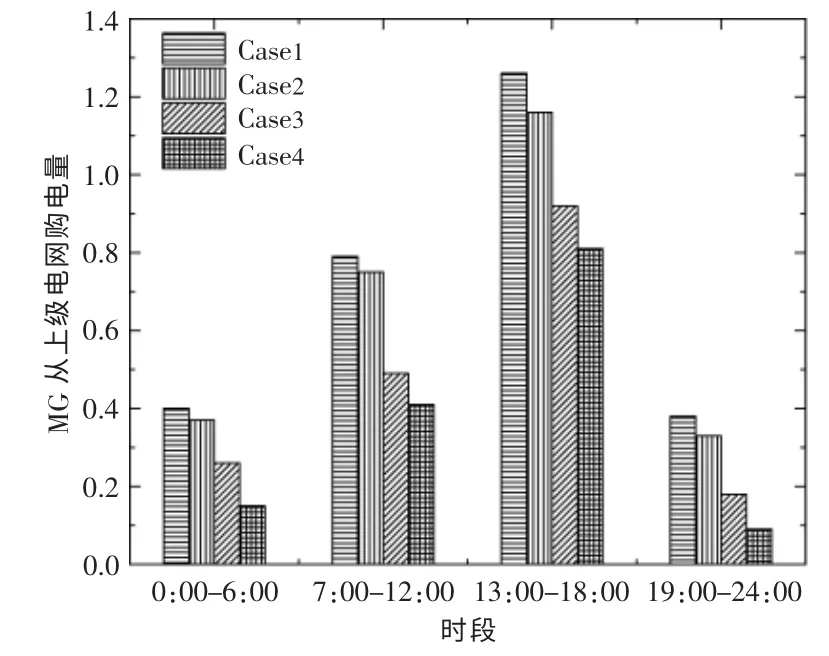
图6 不同算法下MG 从上级电网购电量对比Fig.6 Comparison chart of power purchase from microgrid to superior grid under different algorithms

从图6 中可以看到： 当MG 间无法进行电量交易时，MG 只能从上级电网进行购电，且购电量在中间两个负荷高峰时段较高； 当MG 间可进行电量交易时， 相对于Case1，3 种算法的购电量均有不同程度的下降。 Greedy 算法由于训练效果较差，虽然购电量有所下降，但是效果并不理想；深度Q 学习算法以及Hotbooting Q 交易算法效果较为理想。可见在每个时刻，后两种算法均可以大幅度削减MG 向上级电网的购电量， 减少MG 对上级电网的依赖性。

不同时段下的MG 平均收益值如图7 所示。从图中可以看到： 在各个时刻，3 种算法在收益上的规律与上述分析也保持一致，Hotbooting Q 交易算法在各个时刻的计算结果均为最优；在7：00-12：00 和19：00-24：00，MG 的收益显然低于1：00-6：00 和13：00-18：00， 这主要是因为这两个时段负载需求上升，MG 需要从上级电网购电，从而增大了购电成本，导致收益有所下降。

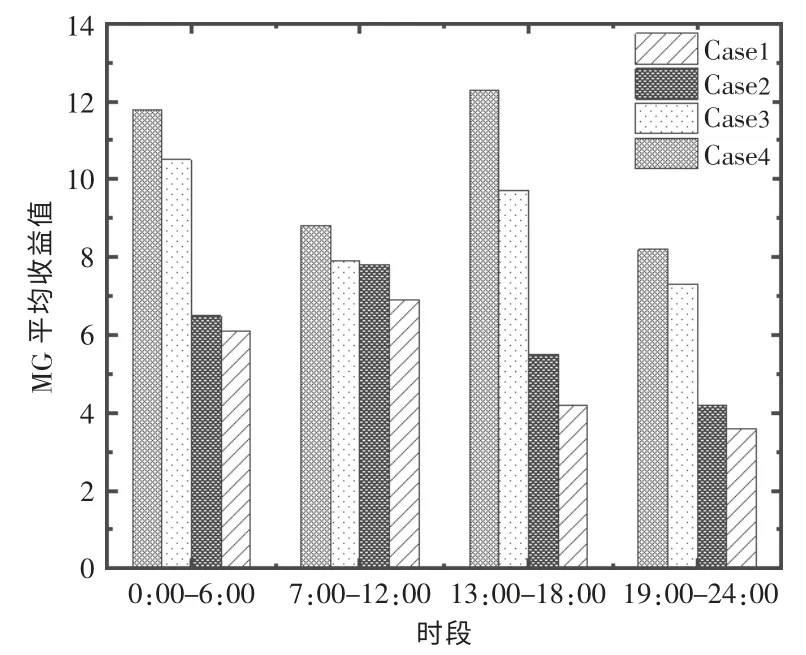
图7 3 种算法下的各时刻收益变化值Fig.7 Change graph of income at each time under three algorithms

由式（18）可知，增益系数的取值将会对MG的电能交易产生影响， 而效益函数主要包括两部分：MG 内存储电量的变化带来的收益变化和MG交易方式的变化带来的收益变化。 通过调节参数可设置两种收益的权重比。

设置β 值为[6，10]，从图8 可以看到，随着β值的增大，3 种算法下的MG 平均收益均有所增加，且深度Q 学习算法以及Greedy 算法下的MG收益值随着β 的变化呈现出近似线性关系。 在整个增益系数变化范围内， 基于Hotbooting Q 交易算法的MG 收益值由9 增加到13.5， 增幅为50%。此外，在不同的增益函数下，Hotbooting Q 交易算法的性能依然比深度Q 学习算法和Greedy算法优秀。

图8 MG 效益随β 值变化情况Fig.8 Schematic diagram of MG benefit changing with β value

4 结论

①多MG 间的电能交易可有效提高MG 用户收益，减轻MG 对上级电网的依赖性，减少与上级电网的交易电量。

②Hotbooting Q 交易算法可加快算法的收敛速度，减少算法前期的学习以及探索时间，提高求解效率。

③与深度Q 学习算法以及Greedy 算法相比，Hotbooting Q 交易算法可显著提高MG 的收益，减少MG 从上级电网的购电量， 所求得的结果在3 种算法中最优。