齿轮箱复合故障诊断方法及其应用研究
大庆油田工程有限公司巴州分公司
齿轮箱作为机械设备中传递动力和扭矩的部件,长时间处于负荷大、转速高和温度高的恶劣工作环境中,其中的零部件极易因疲劳进而引发局部故障。大量的工程实践表明,故障往往不是单独出现,某些故障会诱发其他故障的发生,从而出现复合故障[1]。复合故障是指某些机械零部件出现两个或两个以上相互耦合、相互交叉的故障[2]。不同部位、不同模式的故障信号相互耦合,彼此干扰,给故障诊断工作带来了许多挑战。因此,开展强噪声环境下齿轮箱复合故障诊断的研究具有重要意义。
文献[3]运用局部均值分解(LMD)将复合故障信号进行分解,低频分量提取转轴故障特征,高频分量提取轴承故障特征,实现复合故障诊断。文献[4]提出了一种基于形态分量分析(MCA)和包络阶次谱的复合故障诊断方法,分离变转速工况下齿轮箱滚动轴承和齿轮故障。文献[5]首先将轴承复合故障信号运用VMD 分解为多个模态分量,然后将这些分量进行Hilbert 变换,输入到独立分量分析(ICA)中实现复合故障的分离。
齿轮和滚动轴承是齿轮箱最主要的组件,当齿轮发生局部故障时,齿轮的啮合频率与其谐波频率会被转动频率与其谐波频率调制,获取的故障信号中包含调频-调幅成分;当滚动轴承发生局部故障时,滚动轴承故障零件的固有频率会被其故障特征频率调制,获取的故障信号包含周期性的冲击脉冲。因此,齿轮和滚动轴承的故障特征频率可以作为开展齿轮箱复合故障诊断的重要依据。
1 方法理论
1.1 变分模态分解(VMD)
VMD 中将变分问题描述为约束条件为各模态之和等于输入信号f,寻求k个模态函数,使得每个模态函数的估计带宽之和最小[6]。方法定义本征模态函数为一个调幅-调频信号,其表达式为
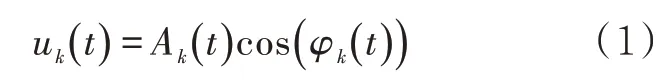
式中:uk(t)可以看作一个幅值为Ak(t)、频率为ωk(t)的谐波信号。
VMD 引入二次惩罚因子α 和拉格朗日乘法算子λ(t),将约束性变分问题变为非约束性变分问题,二次惩罚因子α可在高斯噪声存在的情况下保证信号的重构精度,拉格朗日算子λ(t)加强了约束条件的严格性。扩展的拉格朗日表达式为

1.2 最大相关峭度解卷积(MCKD)
MCKD 以相关峭度为标准,构造有限冲击响应滤波器,使原始冲击信号通过滤波后相关峭度值达到最大,突出被噪声掩盖的周期冲击成分[7]。
选取一个最优滤波器f(l),使相关峭度CKM(T)最大,令:
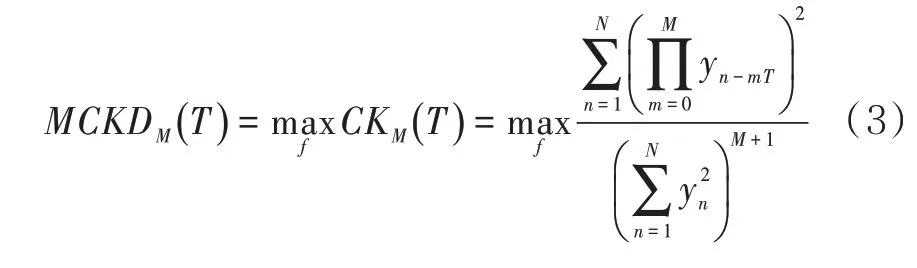
式中:T为冲击信号周期;M为位移数;为滤波器向量,L为滤波器的长度。
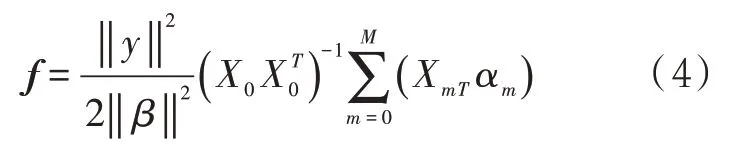
式中:y为滤波后的输出信号,β为输出信号相关向量,XmT是初始信号相关向量。
基于VMD 和MCKD 的齿轮箱复合故障诊断方法步骤如下:
(1)将采集到的齿轮箱复合故障振动信号进行VMD 分解,通过设定不同的模态数,使信号达到最佳的分解效果。
(2)基于互相关准则,筛选与原始信号互相关系数大于0.5 的模态分量进行重构,实现振动信号的降噪。
(3)根据齿轮和滚动轴承故障不同冲击特征频率确定解卷积周期,通过循环迭代最终确定最佳解卷积滤波器长度,运用MCKD 对降噪后的信号进行滤波,分离轴承和齿轮故障特征,实现复合故障诊断。
2 工程应用
在某油田下属作业区开展故障诊断工作的过程中,多次发现往复式注水泵机组传动齿轮箱存在齿轮和轴承复合故障的情况,包括轴承内圈与齿面磨损、轴承外圈与轮齿断裂等。基于现场采集到的齿轮箱复合故障信号,对齿轮箱复合故障诊断展开研究。
已知齿轮箱输入轴的转速为1 450 r/min,输入轴的转动频率为24.17 Hz,输入轴主动轮的齿数为30,中间轴从动轮的齿数为65,振动信号的采样频率fs=42 240 Hz,测点位于输入轴和输出轴轴承座竖直方向,如图1 所示。输入轴轴承为圆柱滚子轴承,轴承的节径D=140 mm,圆柱滚子的直径d0=20 mm,齿数Z=15,接触角α=0°。则根据滚动轴承故障频率公式计算轴承内圈故障频率fi=241.17 Hz,外圈故障频率fo=165.38 Hz,滚动体故障频率fb=178.73 Hz。

图1 测点位置示意图Fig.1 Schematic diagram of measuring point location
将采集的滚动轴承内圈和齿轮齿面磨损复合故障信号进行VMD 分解,当k=4 时信号达到最佳的分解效果,分解后的时域波形及频谱图如图2所示。
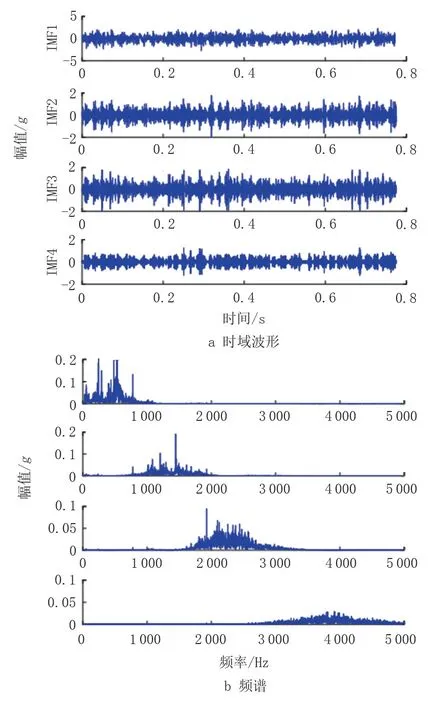
图2 分解后各模态时域波形及频谱Fig.2 Time domain waveform and spectrum of each mode after decomposition
为了达到降噪的目的,滤除噪声干扰,求解分解后各模态分量与原信号的互相关系数,见表1。

表1 轴承内圈和齿面磨损复合故障信号分解后的互相关系数Tab.1 Cross-Correlation coefficient of compound fault signal of bearing inner ring and gear surface wear after decomposition
选取互相关系数>0.5 的模态分量进行信号重构,由表1 可知,选取分解分量IMF1、IMF2 和IMF3 进行重构。
轴承内圈故障的解卷积周期T=fs/fi=175,齿面磨损故障的解卷积周期T=fs/fr=1 748,设定位移数M=7,设定滤波器长度L的搜寻区间为[20,1 000],搜寻步长为20,通过搜寻迭代确定最佳滤波器长度L,最后达到最佳滤波效果。分离后的轴承内圈故障和齿面磨损故障时域波形及频谱如图3 和图4 所示(fm为齿面磨损特征频率,fr为机组的转频)。
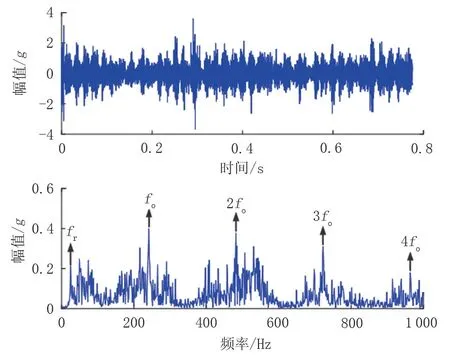
图3 分离后轴承内圈故障时域波形及频谱Fig.3 Time domain waveform and spectrum of bearing inner ring fault after separation
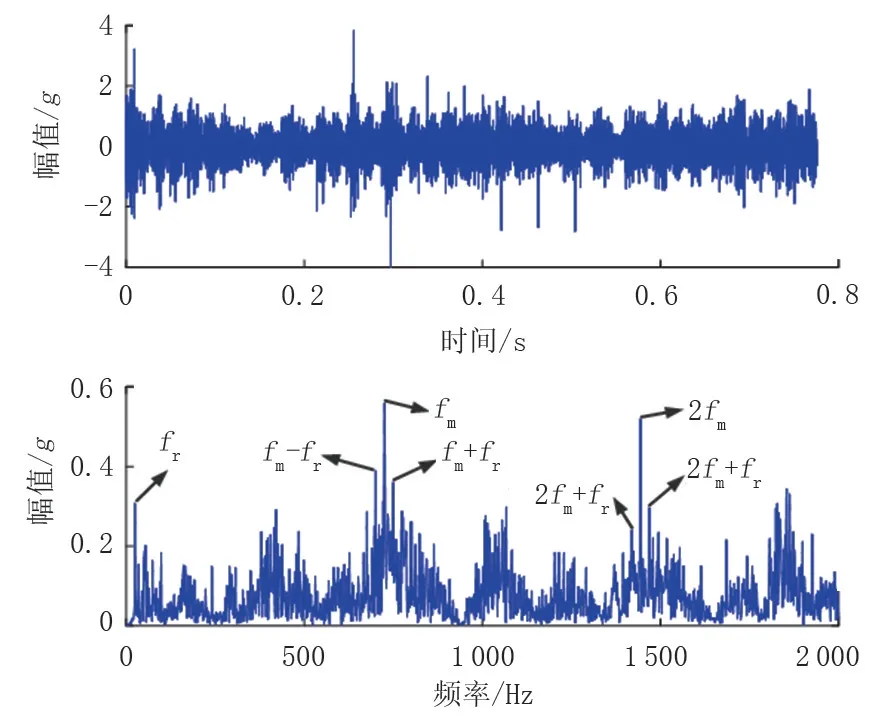
图4 分离后齿面磨损故障时域波形及频谱Fig.4 Time domain waveform and spectrum of gear surface wear failure after separation
由图3 可知,分离后的故障频谱图中轴承内圈故障特征频率及倍频可以清晰分辨。由图4 可知,分离后的故障时域波形中可以清晰分辨故障周期性冲击成分,频谱图中齿面磨损故障特征频率及倍频也可以清晰分辨,且具有调制现象。
将采集的滚动轴承外圈和齿轮轮齿断裂复合故障信号进行VMD 分解,当k=4 时信号达到最佳的分解效果。
求解分解后各模态分量与原信号的互相关系数,如表2 所示。选取IMF1、IMF2 和IMF3 分量进行重构。

表2 轴承外圈和轮齿断裂复合故障信号分解后的互相关系数Tab.2 Cross-Correlation coefficient of compound fault signal of bearing outer ring and gear tooth fracture after decomposition
轴承外圈故障的解卷积周期T=fs/fi=255,齿面磨损故障的解卷积周期T=fs/fr=1 748,设定位移数M=7,通过搜寻迭代确定最佳滤波器长度L,最后达到最佳滤波效果。分离后的轴承外圈故障和轮齿断裂故障时域波形及频谱如图5和图6所示。
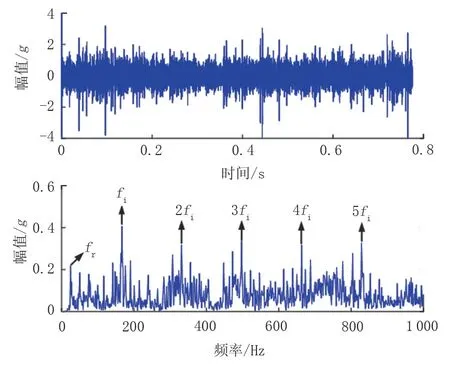
图5 分离后轴承外圈故障时域波形及频谱Fig.5 Time domain waveform and spectrum of bearing outer ring fault after separation
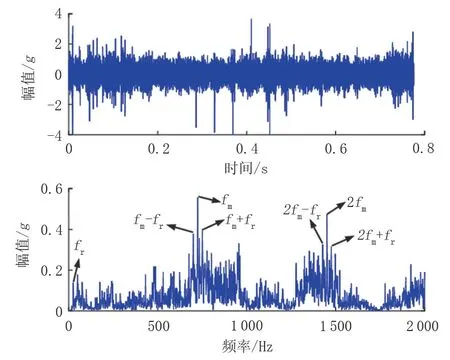
图6 分离后轮齿断裂故障时域波形及频谱Fig.6 Time domain waveform and spectrum of gear tooth fracture failure after separation
由图5 可知,分离后的故障频谱图中轴承外圈故障特征频率及倍频可以清晰分辨。由图6 可知,分离后的故障时域波形中可以清晰分辨故障周期性冲击成分,频谱图中轮齿断裂故障特征频率及倍频也可以清晰分辨,且具有调制现象。
3 结论
针对油田齿轮箱复合故障难以实现精确诊断的问题,提出了基于VMD 和MCKD 的齿轮箱复合故障诊断方法。运用VMD 对故障信号进行自适应分解,滤除噪声干扰;根据轴承和齿轮故障特征频率的不同,运用MCKD 分离轴承和齿轮故障特征,实现齿轮箱复合故障诊断。通过现场工程应用,轴承和齿轮的故障特征频率凸显,表明了该方法的有效性。

