改进BAS-TIMS算法在空战机动决策中的应用

嵇慧明，余敏建，乔新航，杨海燕，张帅文

(1. 中国人民解放军94701部队， 安徽 安庆 246000； 2. 空军工程大学 空管领航学院， 陕西 西安 710051)

随着技术的快速发展，战机性能逐步得到提升，空战对抗也变得异常激烈。空战机动是为了使我机取得最优空战态势，对目标机构成威胁并实施有效的攻击，甚至在我机处于劣势时，通过机动摆脱目标机的锁定，脱离危险[1-3]。当前，空军航空兵在空战决策时，仍以飞行员的自主判断决策为主，在复杂多变的战场环境中，无疑造成飞行员的精力分散，降低机动决策效率和精度。因此，对空战机动决策问题展开研究，实时生成合理、可靠、精确的机动策略则显得至关重要。

目前，用于空战机动决策的智能方法主要有影响图法[4-5]、贝叶斯网络[6-7]、专家系统法[8]、强化学习[9-11]、遗传算法[12-14]及其改进算法[15]等。利用影响图法对空战要素之间的关系进行分析，结合博弈法生成空战机动对策，所得结果较为贴近空战实际，但计算时间长，难以满足空战实时性要求；将客观信息和专家知识融入贝叶斯算法中，可以更好地描述复杂空战环境，从而提高空战机动决策仿真效果，但是对提升空战决策效率没有明显改善；强化学习、遗传算法及其改进算法等进化算法稳定性不够，在应用中存在收敛性差、易陷入局部最优、实时性不够等缺点。

Kaneshige等[16]利用生物学中的免疫机制，将态势-机动视为免疫应答，建立了战术免疫机动系统(Tactical Immunized Maneuver System，TIMS)，可有效提高决策精度和速度，但是在免疫搜索进化时效率较低；Jiang等[17]对自然界中天牛觅食现象进行模拟，建立了天牛须智能搜索(Beetle Antennae Search, BAS)算法，该算法具有良好的搜索适应性，但是搜索时间较长，且全局搜索能力有待进一步提升。若对BAS算法实施改进，并与TIMS进行融合，可以进一步提升算法的搜索收敛稳定性和搜索速度，在实际空战机动决策中更加具有实际应用意义。

本文基于改进BAS-TIMS算法对空战机动对策生成问题展开研究。对传统的机动动作库进行扩充并给出了机动动作控制模型，进一步贴近空战机动实际；利用非参量法对战机机动决策优势进行评估，弥补了参量法的参数多、模型复杂的缺陷；针对天牛须算法全局搜索能力低的缺点，引入了蒙特卡洛概率迭代方法，对BAS算法进行改进，并和战术免疫机动系统融合，使战机机动策略搜索具有一定的方向性，从而进一步提升空战机动决策效率，更好地解决空战机动决策问题。

1 空战机动策略模型

1.1 战机基本机动策略库

目前，空战机动策略集模型主要分成两类：第一类是基于典型空战战术的机动序列，如定常盘旋、蛇形机动、半筋斗、斜筋斗等；第二类是基于战机在三维空间中操纵方式的基本机动动作库，NASA学者设计了7种基本机动动作库[18]——减速前飞、匀速前飞、加速前飞、右转、左转、爬升和俯冲。本文在这7种基本机动动作的基础上，增加了左爬升、右爬升、左俯冲、右俯冲4种机动，对原机动动作库予以扩充，得到了11种基本机动策略，并给出了每种机动策略的控制方法，使得机动更加精细，能够更为全面地反映飞机在三维空间内的运动情况，如图1所示。

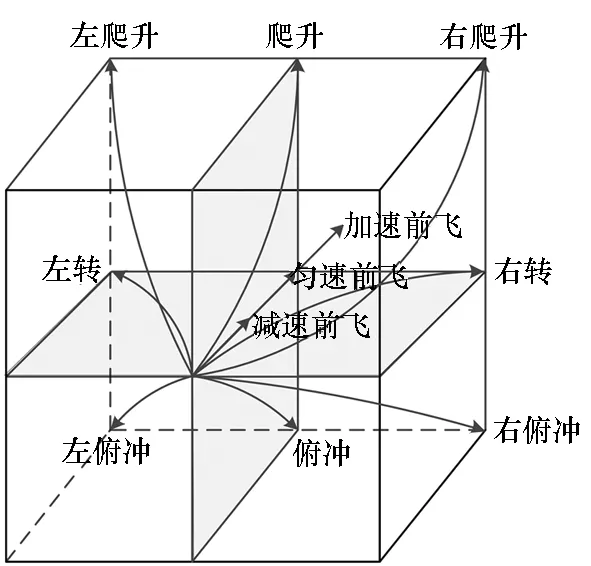
图1 空战机动策略库Fig.1 Air combat maneuver strategy library

1.2 战机基本机动策略控制

为了对机动动作实现精确控制，现将11种基本策略分成3类来研究：平飞机动、俯仰机动和转弯机动。用三自由度的方式对上述11种指挥引导策略建立相应的模型，以nx、ny、γ作为控制变量，nx、ny、γ分别表示切向过载、法向过载和转弯坡度，建立统一的战机机动策略控制模型。

(1)

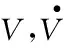
每种基本机动策略的控制量见表1。

对式(1)实施变换，可以将战机控制量转换为更加直观的飞行姿态变化。

(2)

当明确控制量nx，ny，γ的大小以及初始飞行状态时，可对式(2)进行积分，得到控制后战机的新的姿态α，β，V，从而可得战机三维位置坐标的变化率。

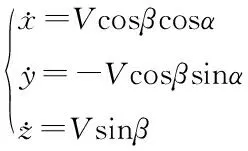
(3)

表1 11种基本机动策略控制量

2 战机机动决策优势评估

战机机动决策的根本目的是使我方战机的空战态势最优，且受到目标机的威胁最小。空战态势优势评估主要有参量法和非参量法两类，非参量法在实际应用中需要大量的参数，可行性不高，因此在传统的距离、高度、速度和角度等空战优势评估指标的基础上，增加了战机性能优势评估指标，用非参量法建立空战优势评价指标体系，如图2所示。

图2 空战优势评价指标体系Fig.2 Evaluation index system of air combat superiority

2.1 距离优势[19]

(4)

其中：D，DRmax，DMmax分别为战机间相对距离、雷达最大探测距离和导弹最大攻击距离；DMkmax，DMkmin分别为导弹最大、最小不可逃逸距离。

2.2 高度优势

(5)

其中：HW，HM分别为我机与目标机的高度；Hbest为战机最佳空战高度，通常可根据战机的高度以查表的方式获得。

2.3 速度优势[20]

(6)

其中：VW，VM分别为我机与目标机的速度；Vbest为我机最佳空战速度。

2.4 角度优势[21]

(7)

其中：Sφ，Sq分别为方位角优势和进入角优势；λ1，λ2为权重系数；λ1+λ2=1，具体取值通常由专家打分给出，本文中取λ1=λ2=0.5。

(8)

其中：φ，q分别为目标方位角和我机进入角；φRmax为雷达最大搜索方位角；φMmax为空空导弹最大离轴发射角；φMkmax为空空导弹不可逃逸区最大偏角。

(9)

当φ>90°时，令φ′=180°-φ；当φ<-90°时，令φ′=-180°-φ，并以φ′替代原式中的φ。当q<φ≤0时，令q′=q+360°；当q>-φ>0时，令q′=q-360°，并以q′替代原式中的q。

2.5 性能优势

战机的空战性能通常用对数公式表示。

C=[lnB+ln(∑A1+1)+ln(∑A2+1)]ε1ε2ε3ε4

(10)

式中：B，A1，A2分别为战机的机动性参数、火力打击能力参数和探测能力参数；ε1，ε2，ε3和ε4分别为战机的操纵效能系数、生存能力系数、航程性能系数和电抗能力系数,且εi≠0(i=1,2,3,4)。这7个参数可以根据飞机的相关性能参数获得，具体计算方式参考文献[22-23]，对于典型的作战飞机型号，可通过查表的方式获取。此处不再详述。

根据式(10)可建立战机性能优势函数：

(11)

其中：CW，CM分别为我机与目标机的空战性能，SP∈(0,1)。

2.6 战机综合优势

SSC=ωDSD+ωHSH+ωVSV+ωASA+ωPSP

(12)

式中，ωD，ωH，ωV，ωA，ωP分别为各项指标对应的权重。传统的权重值通常由专家打分法求取，有着较强的人为主观性。为了提高信息处理的客观性，本文采用文献[24-25]中的改进粗糙集理论方法求取指标对应的权重。

(13)

式中，φ(i)为单个属性i的重要度表示，具体计算步骤可参考文献[24-25]。

3 基于改进BAS-TIMS的空战机动对策生成

3.1 天牛须搜索算法

天牛须搜索算法是在2017年提出的一种新的智能搜索算法，其生物学原理是对自然界中天牛觅食现象的模拟。天牛觅食时，在不知道食物位置的情况下，会通过左右两只触角对食物的气味强度进行比较，从而确定下一步的飞行方向，直至找到食物的位置，如图3所示。

图3 天牛觅食示意图Fig.3 Schematic diagram of beetle finding food

在对天牛觅食过程模拟时，食物的气味强度可以作为待优化问题的适应度函数，前进方向作为搜索的选择结果，前进距离作为仿真步长，则天牛的觅食过程可以抽象成相应的算法模型，描述如下：

1)天牛是在三维空间内移动，为了提升模型的适用度，现将其范围扩展到任意维空间，假设天牛可以在一个任意维度的空间内搜索；

2)为了更好地描述天牛的觅食搜索过程，现将天牛的身体视为一个质点，天牛须位于两侧，且以质点为中心对称，则左右两侧天牛须的长度之和即为天牛的身体宽度；

3)天牛每一次搜索后的前进距离和身体宽度成一定的比例；

4)假设天牛在每次前进后头的朝向随机，则天牛须的方向也随之成为随机变量；

5)气味在整个空间里分布是连续变化的。

3.2 BAS算法搜索策略及改进

运用BAS算法对目标实施搜索时，首先需要初始化参数并随机生成天牛方向，然后计算天牛的左右须位置及其适应度值，接着通过适应度函数值判断前进方向，满足结束条件后输出最优值。具体如图4所示。

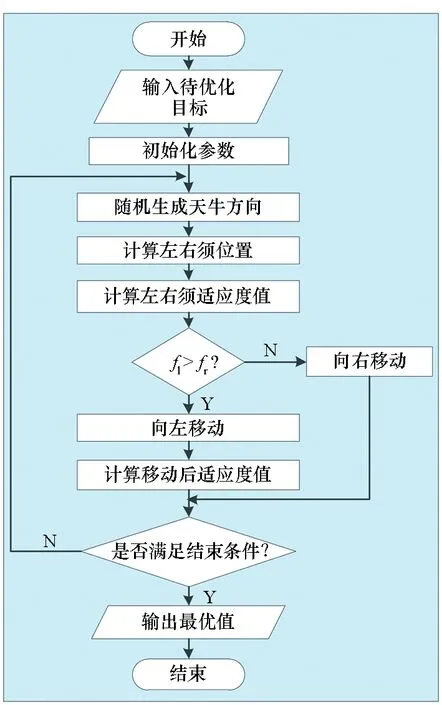
图4 天牛须搜索算法流程Fig.4 Flow of BAS algorithm

步骤1：初始化相关参数。对于k维空间内的最优化搜索问题，设天牛的质心为x，左须向量为xl，右须向量为xr，x、xl和xr均为k维向量。

步骤2：对天牛的方向向量予以定义：

(14)

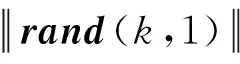
(15)

其中：xt为迭代t次后天牛的质心位置，dt为迭代t次后左、右须之间的距离。

步骤3：判断前进方向。分别计算天牛左须xl和右须xr的适应度函数值fl和fr，故天牛的前进方向为：

xt=xt-1-bδtsgn(fl-fr)

(16)

式中：δt为第t步时天牛的移动步长。sgn(C)为符号函数，当C<0时，sgn(C)=-1；当C>0时，sgn(C)=1；当C=0时，sgn(C)=0。

步骤4：计算天牛移动后新的适应度函数值，并对天牛的步长和左右须之间的距离进行更新。

(17)

其中：attd为距离衰减系数，attδ为步长衰减系数。一般情况下，初始时刻天牛的搜索步长大，随着距离气味源的距离拉近，搜索步长逐渐减小。

步骤5：判断过程是否满足终止条件，若满足，则输出对应的选择方案，否则返回步骤二，直至满足结束条件。

BAS算法在搜索时具有很强的适应性，每次迭代后，将进化个体视为正在觅食的天牛，计算算法在移动后的适应度函数值，并与移动前的算法适应度函数值进行对比，若移动后的适应度函数值更优，则予以移动，否则不移动。具体搜索模型为：

(18)

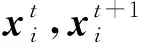
利用BAS算法对问题的最优解实施搜索，具有搜索速度快等优点，但是在迭代过程中容易陷入局部最优。为了提高BAS算法的全局搜索能力，引入模拟退火算法中的蒙特卡洛准则，对BAS算法进行改进。图5为搜索选择概率图，在每次搜索选择时，以概率p接受较差解，从而提升BAS的全局搜索能力。且有：

(19)

其中：f(xt)表示第t次迭代后预计适应度函数值；f(xt-1)表示第t-1次迭代后的适应度函数值；k为衰减系数。

由计算公式可以看出，随着迭代次数的不断增加，选择较差解的概率值p将越来越小。

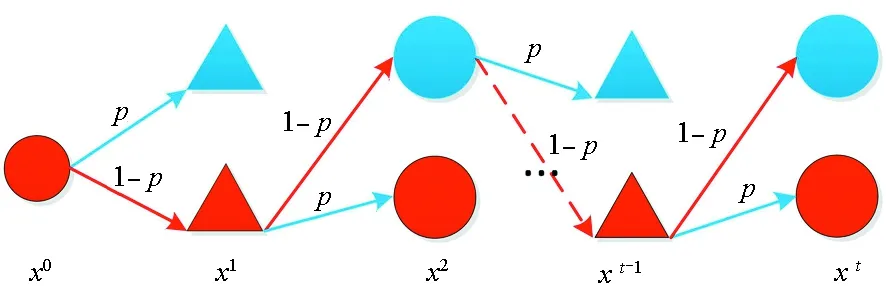
图5 搜索选择概率图Fig.5 Search selection probability

3.3 战术免疫机动系统模型

免疫是一种科学的内建防御体系，存在于所有的生物中，以减弱外部攻击。生物免疫系统在免疫应答产生的过程中，接收来自抗原-抗体复合物的连续反馈，从而产生越来越特异的抗体应答。它可以记住先前的遭遇是如何被击败的，从而在后期发生类似的遭遇时能够快速做出反应，这是一个学习范式，能够开发解决方案，并不断增加系统的精度。

对生物免疫系统进行数学化描述，在人工免疫算法的基础上，建立了战术免疫机动系统，该系统良好的自学习能力与实时性能，能够较好地克服空战中影响战机决策的不确定因素，从而对求解空战对策的实时生成问题有着良好的适配性。系统主要由以下几个部分组成。

3.3.1 机动动作库的构建

在第1节中，建立了11种基本指挥引导策略，并对其控制方法加以描述。基于控制变量nx，ny，γ及其范围，可以构建战机的机动动作库：

Mk=[nx,ny,γ]∈[-2,2; -5,7; -0.5π,0.5π]

(20)

在三自由度控制模型中，当控制变量的值确定时，战机的机动动作也唯一确定。例如，当(nx，ny，γ)=(0,1,0)时，战机做匀速前飞机动。

3.3.2 机动策略编码

将战机的机动策略存于24位二进制字符串中，该字符串被分成四个部分：6位(1～6)代表战机识别码，6位(7～12)代表控制变量nx，6位(13～18)代表控制变量ny，6位(19～24)代表控制变量γ。具体如图6所示。

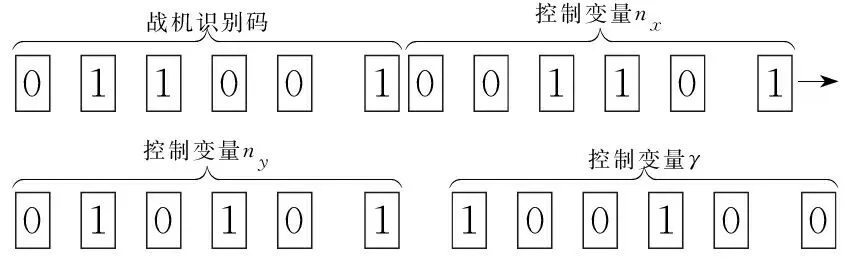
图6 机动策略编码示意图Fig.6 Schematic diagram of maneuver strategy coding

nx的数值精度为1/16，ny的数值精度为3/16，γ的数值精度为π/64。

3.3.3 机动策略评估

建立机动动作库后，可以对后续的机动策略充分预测，并构造亲和度函数对机动策略实施评估。基于式(12)，机动策略评估的亲和度函数为：

fk(C)=α·S′k(G)+(1-α)·[1-T′k(G)]

(21)

式中，fk(C)表示战机做机动k时的亲和度函数值，S′k(G)表示战机做机动k时的态势优势值，T′k(G)表示战机做机动k时受到目标机的态势威胁值，α为态势优势重要度系数。

3.3.4 空战态势编码

空战态势主要包括目标机和我方战机的位置信息、航向、高度、速度等，在战术免疫机动系统中，为了实现机动策略与空战态势间的免疫操作，需要对空战态势进行编码，选取以下6个特征进行编码：战机间距离、相对高度、目标方位角、航向交叉角、我方战机速度、目标机速度。

相对高度的范围为 [0 m，4800 m]，精度为150 m；目标方位角范围为 [0°，360°]，精度为6°；航向交叉角的范围为 [0°，360°]，精度为6°；我方战机和目标机的速度范围为 [0 m/s，400 m/s]，精度为12.5 m/s。利用上述方法对其进行编码操作。

3.3.5 机动策略选择

将战机当前的机动状态作为初始状态，利用相应的算子对机动策略进行选择，最终将亲和度函数值最大的机动策略作为最优选择。当发现成功的机动动作时，将其机动策略以及相应的空战态势特征放入相应的数据库中，为后续的模型进化提供依据。

3.3.6 机动策略解码

首先根据选择的机动策略的编码，计算出控制变量nx，ny，γ的值，然后由表1中的11种指挥引导策略控制量范围得出我方战机的基本机动策略，接着根据式(2)、式(3)计算机动后我方战机的位置和机动后的航向、速度和高度。

3.4 改进BAS算法与TIMS模型的融合

改进的天牛须搜索算法虽然具备良好的全局搜索能力，但是在每次搜索时，计算复杂度是相同的，若对机动动作进行精确化搜索，则计算量十分庞大，影响收敛速度；TIMS模型能够随着迭代次数的增加对机动策略选择库进行扩充，在后续选择中降低计算复杂度，但是对于之前未出现的态势，进化搜索时收敛速度较慢。将改进BAS算法和TIMS模型进行融合，并在仿真实验中对融合算法的优越性进行检验，具体过程如图7所示。

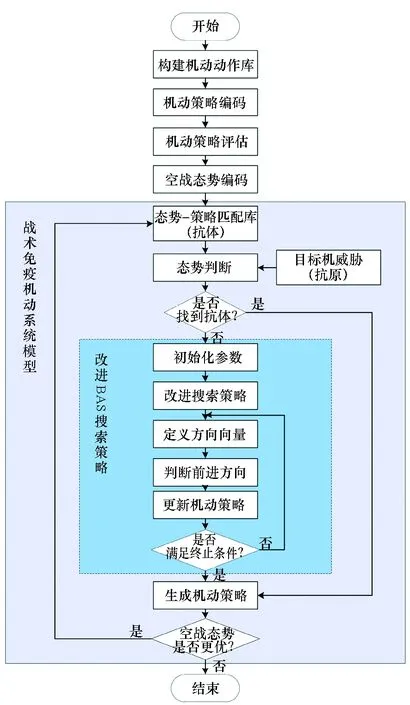
图7 改进BAS算法和TIMS模型融合Fig.7 Fusion of improved BAS algorithm and TIMS model

3.5 空战机动对策生成

空战时，敌我双方都在试图通过机动使目标机对己方的威胁最小，同时尽量使己方获得最优空战态势，构成攻击条件对目标实施打击。因此，需要根据敌我双方的空战态势实时生成机动决策方案，基于上述的改进BAS-TIMS，生成我方战机的机动对策，其过程如图8所示。

步骤1：获取我方战机和目标机的空战态势数据，并做格式化处理。

步骤2：对空空导弹弹道进行仿真，并计算出实时攻击线的距离，判断是否构成攻击条件，若满足则对目标机实施攻击，否则转入下一步机动。

步骤3：对我方战机的空战态势和受到目标机的威胁实施评估，并在此基础上利用改进的BAS-TIMS算法求解下一步的机动策略。

步骤4：机动完成后，转入步骤1，反复迭代生成机动策略，直至我方战机对敌方构成攻击条件并发射导弹。

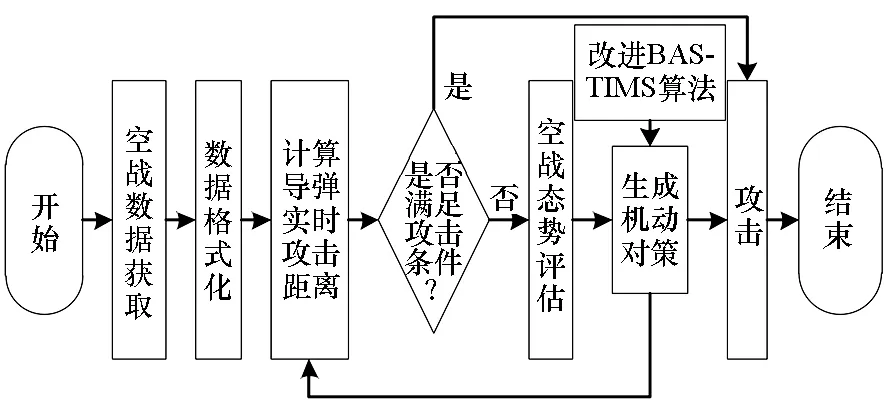
图8 空战机动对策生成Fig.8 Generation of air combat maneuver countermeasures

4 算例仿真分析

4.1 算例仿真

为了验证本文算法在空战机动决策中的有效性，现以敌我一对一空战对抗为背景设计算例进行仿真。初始条件：我机初始位置坐标为(0 km,40 km,6200 m)，航向135°，速度900 km/h；目标机初始位置坐标为(70 km,30 km,6000 m)，航向330°，速度800 km/h。假设敌我双方战机选择同一型号战机，经计算，战机综合优势的各项指标对应权重ωD，ωH，ωV，ωA，ωP分别为0.181，0.181，0.189 7，0.212 7，0.235 6。该型战机的性能优势为0.680 9，雷达最大搜索角φRmax=80°，空空导弹最大离轴发射角φMmax=50°，空空导弹不可逃逸区最大偏角φMkmax=30°，雷达最大探测距离DRmax=120 km，导弹最大攻击距离DMmax=60 km，导弹最大、最小不可逃逸距离分别为DMkmax=30 km、DMkmin=5 km。态势优势重要度系数α取0.7，设仿真步长为5 s，仿真时长为300 s。初始时刻，TIMS模型库中置入1000条实际空战训练的机动序列。当敌我双方均采用本文改进算法策略实施机动时，仿真结果如图9所示。

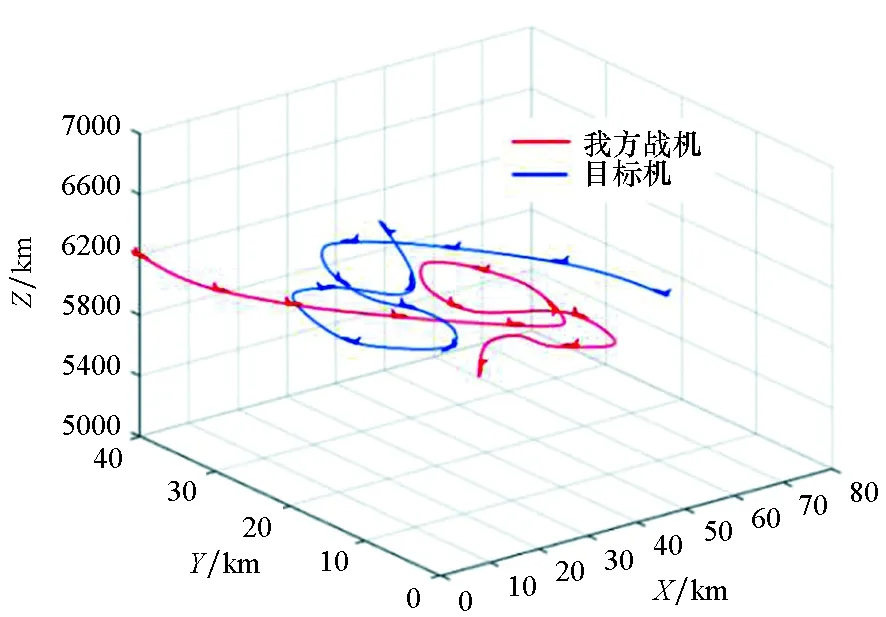
图9 空战对抗三维轨迹Fig.9 Three-dimensional trajectory of air combat

图9在水平面上的投影如图10所示。

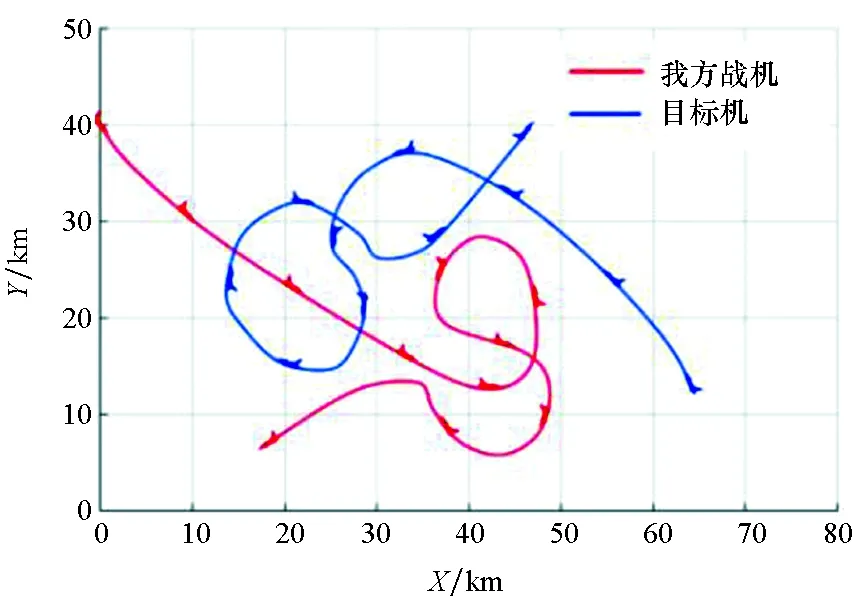
图10 敌我双方空战对抗轨迹水平面投影Fig.10 Plane projection of air combat trajectory

我方战机与目标机对应的机动策略切向过载nx、法向过载ny、转弯坡度γ的变化分别如图11所示，高度和速度变化如图12所示。

图9～12对敌我双方的空战轨迹和机动策略参数进行了描述。初始阶段，我方战机相对目标机在高度和速度上具有一定的优势，角度上处于劣势，通过左转机动，试图化解角度劣势；在一段时间的调整后，我机通过左转机动，对目标进行攻击，并不断调整高度和速度以保持自身优势，目标机也实施大坡度转弯机动，试图摆脱我机的攻击，第一次攻击占位完毕后，我方战机迅速左转回撤，为下一波次的攻击做准备，目标机也积极实施机动，试图在摆脱我方战机的攻击后，通过机动对我方战机构成威胁。综上所述，我方战机和目标机都在积极机动占位，试图使己方保持空战态势优势，并对目标构成威胁。敌我方战机空战态势优势随时间的变化如图13所示。

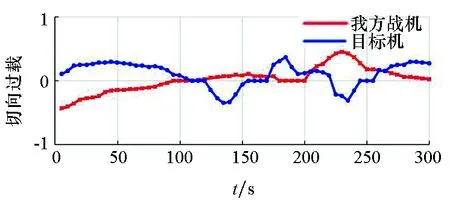
(a) 切向过载(a) Tangential overload

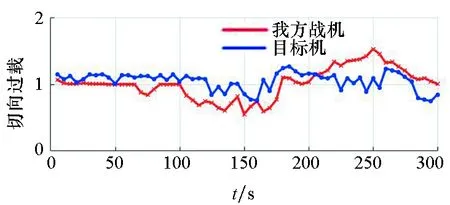
(b) 法向过载(b) Normal overload

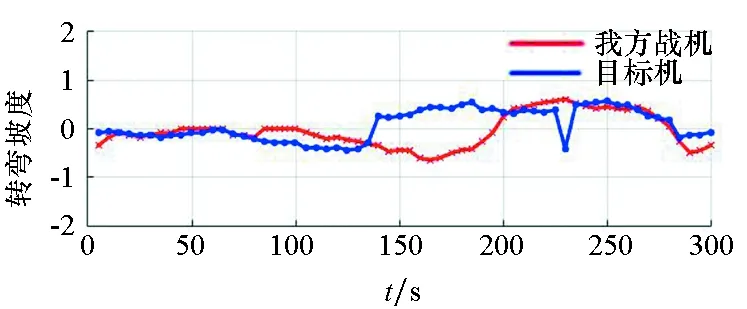
(c) 转弯坡度(c) Turning slope图11 切向过载、法向过载和转弯坡度随时间的变化Fig.11 Changes of tangential overload, normal overload and turning slope with time

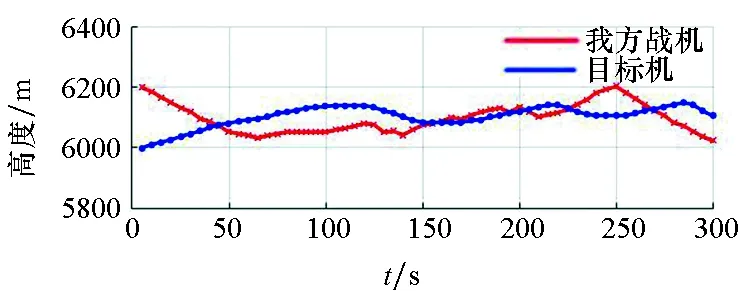
(a) 高度(a) Atitude

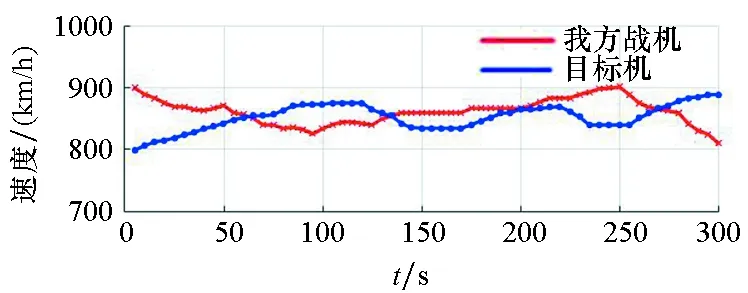
(b) 速度(b) Velocity图12 高度和速度随时间的变化Fig.12 Changes of a titude and velocity with time

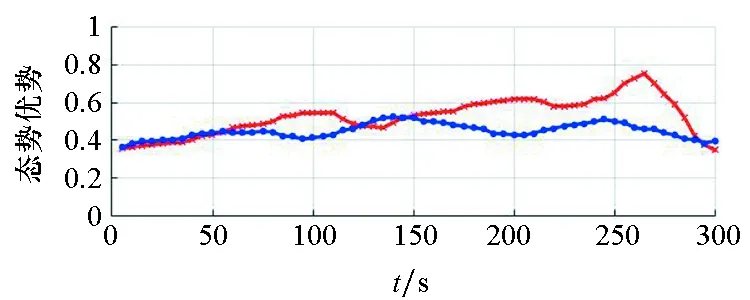
图13 空战态势优势随时间的变化Fig.13 Changes of air combat situation superiority with time

由图13可以看出，初始阶段，我方战机相对处于劣势，通过合理的机动决策，不断增大态势优势；目标机在态势变弱后，也开始实施机动来增强自己的空战态势。证明了改进BAS-TIMS算法生成的空战机动决策能够将己方的劣势地位转化成优势地位。

为了进一步验证改进BAS-TIMS算法的可靠性和有效性，现选取文献[26]中的博弈论方法和文献[27]中的改进共生生物免疫进化算法进行比较。选取上述算例中第250 s处的空战态势作为输入，对3种算法分别迭代50次后，其收敛精度对比如图14所示。

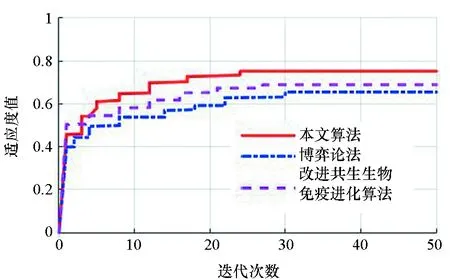
图14 3种算法收敛过程对比Fig.14 Comparison of convergence processes of 3 algorithms

将3种算法分别计算50次，算法最优值和收敛时间对比见表2。

表2 3种算法最优值和收敛时间

综合图14和表2可知，本文算法收敛速度明显快于博弈论法和改进共生生物免疫进化算法，且收敛时适应度值也高于其他两种算法。验证了本文所提改进BAS-TIMS算法能够更好地解决空战机动决策问题。

4.2 算例对比分析

为了检验改进算法的优越性，现选取一静态飞行数据作为目标机的机动轨迹，分别用改进BAS-TIMS算法、传统BAS算法和传统TIMS算法的计算结果与目标机展开对抗。初始时刻，我机位置坐标为(92 km, 27 km, 5800 m)，航向270°，速度900 km/h；目标机位置坐标为(2 km, 26 km, 5400 m)，航向90°，速度800 km/h。静态仿真条件同上。仿真结果如图15所示。

图15 3种算法空战对抗三维轨迹对比Fig.15 Comparison of 3D trajectories of air combat confrontation with three algorithms

图15在水平面上的投影如图16所示。

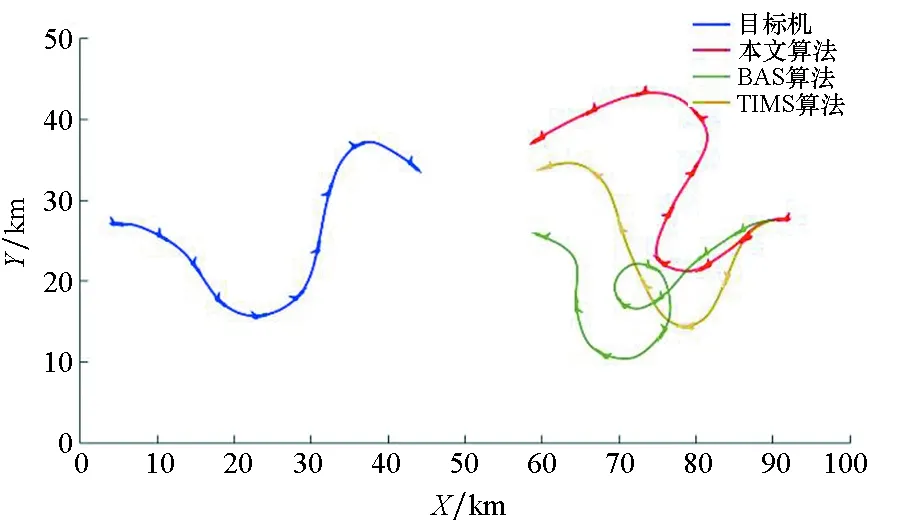
图16 3种算法空战对抗轨迹水平面投影Fig.16 Plane projection of air combat trajectory with three algorithms

3种算法的空战态势优势随时间变化的对比结果如图17所示，3种算法每次迭代的收敛时间对比结果如表3所示。

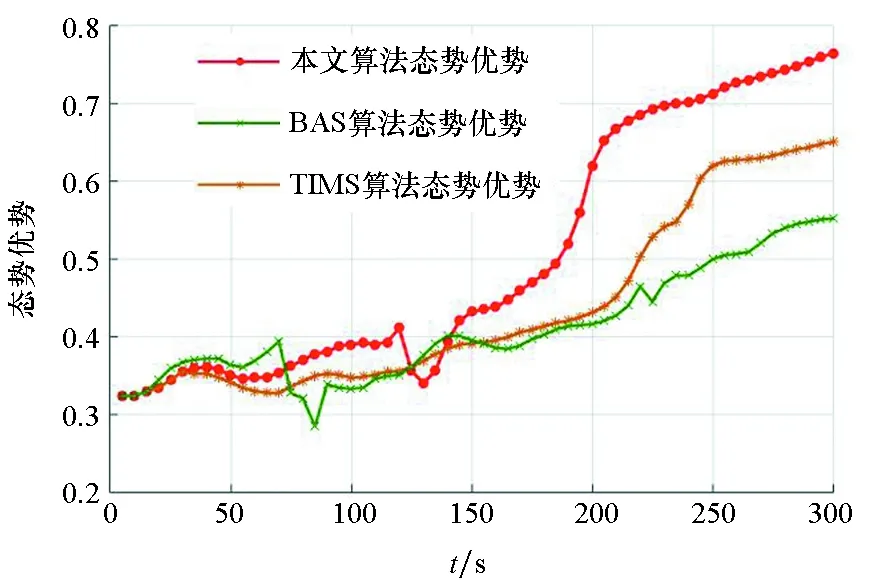
图17 3种算法战机空战态势优势随时间的变化Fig.17 Changes of air combat situation superiority with time based on three algorithms

结合图17及表3，可以得出本文BAS算法计算的机动策略明显优于传统的BAS和TIMS算法，且收敛速度也明显得到提升，进一步证明了本文算法的优越性。

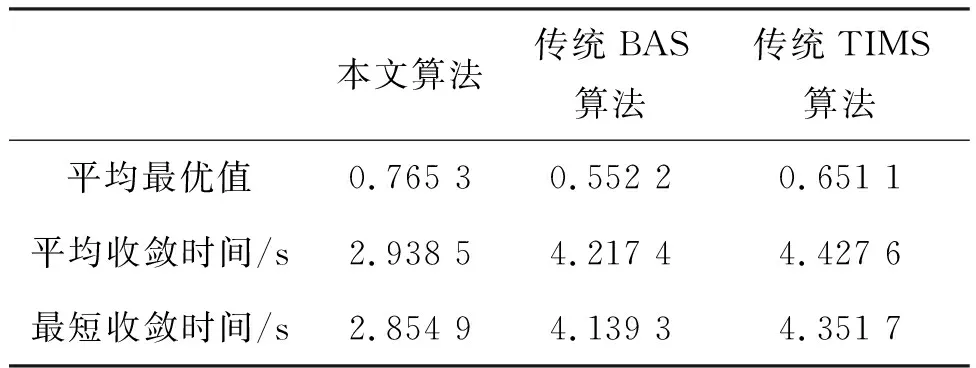
表3 3种算法最优值和收敛时间

5 结论

本文主要对空战机动决策问题展开研究，对天牛须搜索算法进行改进，并与战术免疫机动系统融合，采用改进的BAS-TIMS算法对空战机动策略进行解算，对我方战机的机动进行优化决策。

1) 通过算例仿真，发现战机能够在自身处于劣势时，及时实施机动，增大空战优势，并减弱目标对自身的威胁，验证了改进BAS-TIMS算法的有效性。

2)通过与博弈论方法、改进共生生物免疫进化算法、传统BAS算法和TIMS模型算法结果对比，验证本文算法在适应度最优值、收敛速度以及运行时间上都具有一定的优势。

着眼于未来多机型、多机种、多批次的编队协同作战发展趋势，下一步将在主要工作的基础上，重点研究战机间的战术协同机动，为多机协同空战机动对策生成问题提供理论依据。