对测量不确定度定义的探讨

乔新愚

（工业和信息化部电子第五研究所计量检测中心，广州 510610）

测量不确定度在我国已经推广30多年了，但很多计量人员对不确定度的理解始终感到模棱两可、一知半解，更不用提正确评定和应用了。不少业内人士包括一些行业专家甚至认为，测量不确定度纯属是玩概念，其本质就是误差范围，而且概念模糊、评法混沌，严重干扰了计量工作秩序。为什么会出现这种状况？究其原因在于我国现行规范（包括各类教材、文件）对测量不确定度的定义存在表述含糊和不完善之处。

1. 定义不完善之处

两份权威文件对测量不确定度的定义表述如下。

在JJF 1059.1—2012《测量不确定度评定与表示》中这样定义：根据所用到的信息，表征赋予被测量值分散性的非负参数[1]。

在《测量不确定度表示指南》中这样定义：表征合理地赋予被测量之值的分散性，与测量结果相联系的参数[2]。

这两个定义基本一致（严格来说，第二个定义对测量结果的表述有问题，但不是本文讨论要点，故不展开论述）,都是强调由于测量不完善和测量者认识不足，导致被测量值具有分散性，即每次测得的结果不是同一值，而是以一定的概率分散在某个区域的多个值，测量不确定度就是表示这个分散性。说的更明白一点，评定出来的测量不确定度大小代表了分散区间的半宽。

那么，被测量的真值和这个区间有什么关系呢？定义显然没有给出答案。对于这个问题，业内有如下两种观点。

观点一：目前，所有的规范和绝大多数教科书在解释测量不确定度概念时，都从测得值的分散性入手，回避了测量不确定度大小与真值之间的关系[3]。因此，很多人认为，测量不确定度 的大小仅仅表示多次测量所得值的分散程度，不代表测得值 （被测量真值的估计值）是否接近真值。显然, 该观点 “严扣”测量不确定度的定义。

观点二：测量不确定度规定了一个区间，被测量真值以较大概率(一般取95%或99%)落在区间内（注意, 对于按修正值使用的仪器，测得值 经过修正变成 ，被测量真值以较大概率落在区间 内）。显然，该观点明确地建立了测量不确定度 、测得值 与真值之间的关系[4]。但是，这种观点在测量不确定度的定义中没有体现。

我们知道，测量不确定度 是考虑了各种主要不确定度分量来源，经过合成并扩展评估出来的，其中，重复性是众多不确定度分量之一，代表的是测量条件不变，多次测量同一变量所得值的一致程度（即分散程度）。按照前文测量不确定度的定义（测量不确定度表征测量值的分散性）,很容易让人把测量不确定度和重复性画上等号。但重复性仅仅是测量不确定度的一部分, 而且在数值上也比测量不确定度小。因此，把测量不确定度定义成测量值分散性，存在明显逻辑错误。

另一方面，从使用角度来看，我们采用一个参数的测量值，不仅仅关心该测量值的分散程度，更关心的是被测参量的真值到底落在哪个范围。某个测得值，即使它的分散性很小，但如果它与真值之间的关系不清楚，不能通过这个测得值及其测量不确定度判定被测量真值所处区间，那么这个测得值可以说毫无使用价值。而测量不确定度就是定量表明被测量的真值以较大概率落在范围之内，这样，在采用该测得值时才能做到心中有数。我们日常工作中考虑不确定度进行合格判定时，潜意识里就是基于这一思想。

2. 合格判定中的测量不确定度

在实际进行产品合格判定时，当测量不确定度不满足 时，需要考虑测量不确定度对合格判定的影响。图1显示了合格判定常遇到的八种情况。图中圆点代表测得值，圆点到上/下短杠的距离代表测量不确定度 ,上下规格线之间的距离代表公差T。可判定产品A合格, D超差, B和C有可能超差, 也可能合格。

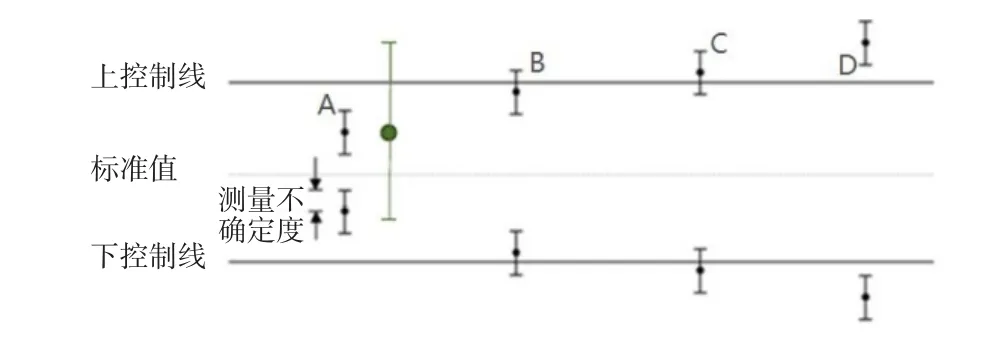
图1 测量不确定度在合格判定中的作用

之所以判定A合格，是因为A的真值存在区间（即A上下短杠之间）在公差带内；判定D不合格，是因为D的真值所在区间在公差带外。B、C真值有可能在公差带内，也可能在公差带外，所以不能判定。对于这种不能判定的情况，需要使用更高级别的仪器（测量不确定度更小）进行测量后再做判定。

如果按照前文第一种观点，测量不确定度仅仅是表示测量结果分散程度，不代表测得值 是否接近真值，不表明真值所在区间，那么产品的实际尺寸（即真值）到底在不在公差带内将无法确定，进而根本无法判定产品是否合格。这将推翻现行产品合格判定的理论基础。

对于考虑不确定度进行仪器合格[5]判定，可参考JJF 1094—2002《测量仪器特性评价》，该规范中推荐的方法也可旁证本文观点二。

3. 真值存在的区间

其实，这一点都不矛盾，反而是客观事实。的确，被测量真值只有一个，在一定的包含概率下，其存在区间也只有一个。用完全相同的测量方法，不同的人或同一个人不同次数的测量，会评估出多个真值可能存在区间，但真值到底在哪个区间呢？答案就是，真值存在于这诸多可能区间的重叠部分，即图2中的灰色阴影部分。

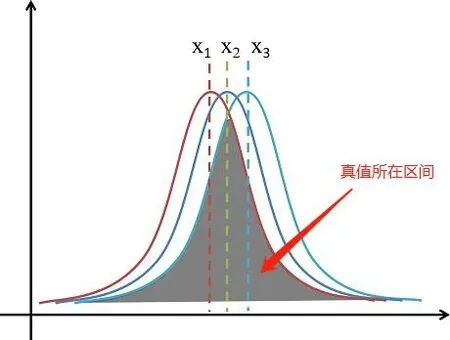
图2 真值所在区域示意图

4. 结论

综上所述，现行测量不确定度的定义仅仅表达出测量值分散性这个特性，没有明确表示测得值、被测量真值与测量不确定度之间的关系，在实际工作中，给广大计量工作者带来很大的迷惑和困扰。所以说，这个定义是不够准确、不够完善的。个人认为，准确完善的测量不确定度定义应该是：根据所用到的信息，表征被测量值分散性的非负参数，被测量真值以较大概率分布在测得值与该参数确定的区间之内。