基于强化学习的功率与信道联合干扰方法研究*

张双义，沈箬怡，陈学强，田 华，张 潇，杜吉庆

（1.中国人民解放军陆军工程大学 通信工程学院，江苏 南京 210000；2.中国电子科技集团公司第二十八研究所，江苏 南京 210007；3.中国人民解放军32753部队，湖北 武汉 430010）

0 引言

飞速发展的无线通信技术导致频谱资源越来越稀缺，用户之间用频争夺越来越激烈，尤其在军事领域的频谱争夺已逐渐成为战争重要作战样式[1-2]。近年来，人工智能技术飞速发展，为通信领域的电磁频谱对抗提供了新的思路[3]。智能抗干扰目前已经有了很多研究[4-6]。文献[4]提出了一种在动态衰落环境中基于强化学习的信道选择抗干扰算法。文献[5-6]作者利用Q学习找到最佳通信信道来躲避干扰，其中文献[6]基于USRP设备搭建了抗干扰平台并验证抗干扰算法有效性。文献[7-8]充分利用了深度学习和强化学习的双重优势，实现了快速有效的抗干扰信道选择。此外，文献[9]提出了一种基于时间和信道选择的联合抗干扰策略，从多个维度对抗干扰决策进行了优化。

然而，通信干扰作为攻击方的主要对抗样式[10-11]，干扰技术仍然停留在传统的干扰方法上，干扰方式过于依赖先验信息[12]，难以根据环境自适应调整自身干扰策略，如传统频域干扰和功率域干扰。频域干扰方式有固定频率干扰、扫频干扰以及梳状干扰等。这些干扰模式单一且需要预先设定工作模式，用户可以轻易发现干扰并通过跳频来躲避，干扰效果下降。而单一功率域的干扰又会造成功率消耗过大且容易暴露位置，增加装备技术复杂性[13]。同时，根据文献[14-15]，用户可以根据接收到的干扰机能量值对其进行定位，然后采用相关技术减弱干扰信号[16]，导致干扰效率大大降低。

为实现精准高效干扰，提高干扰机的智能性十分必要，尤其是利用智能学习解决动态未知环境下的实时干扰决策问题。近年来，不少学者在智能干扰领域也取得了一些突破[17-19]。文献[17]利用深度学习方法探索通信发射机的频率变化规律，然后实施精准干扰。文献[18]则提出了一种频率域的智能干扰算法，干扰机可以通过感知并学习对方信道切换规律达到跟踪干扰的目的，同时证明了算法可以收敛到最优干扰策略。文献[19]提出了一种功率域智能干扰算法，干扰机可以根据对方通信用户工作状态自适应调整自身功率进行干扰，并且能够收敛到最佳干扰策略。但是，以上工作都是聚焦单一域内的干扰方式，在复杂电磁环境中的干扰效果较低。例如，一旦通信用户在功率域进行调整，单纯的信道干扰将无法保证干扰效果。同样，用户单纯的功率自适应调整也无法应对频域内的改变，且上述工作并没有考虑干扰机被定位问题。综上所述，单一功率域干扰一般是阻塞式干扰，实现简单，但是功率低时效果差，功率高时易暴露自己；频率域干扰技术难度高，带宽不大，窄带干扰为主，目标明确。人们希望既能够调整功率降低暴露自己的概率，又能够调整信道进行有针对性的干扰并提高干扰效果，所以本文提出了基于功率和信道的联合干扰优化算法。

智能干扰面临的挑战主要有：（1）干扰机必须具备在线持续学习能力，根据环境动态变化不断调整自身干扰策略做出最优干扰决策；（2）单一频率或功率域干扰难以达到最好的干扰策略，造成资源浪费，必须扩展干扰维度，提高综合干扰效率；（3）干扰机在干扰时会被对方侦察能量进行定位，因此选择最佳干扰功率十分必要。

综上，本文提出了一种功率与信道联合干扰方法。首先将动态环境中的干扰决策问题建模成一个MDP问题，其次通过强化学习求解。算法优化目标是最大化降低通信用户吞吐量，并降低干扰机被定位概率，达到最优干扰策略。因此，本文主要贡献如下：（1）构建基于MDP的多域智能干扰算法，提升复杂环境中的干扰效果；（2）考虑干扰机被定位问题，通过功率优化降低干扰机被发现概率。

本文主要内容作如下安排：第1节给出系统模型并进行系统建模；第2节基于强化学习提出功率与信道联合干扰算法；第3节给出所提算法仿真结果和相关分析；第4节对本文进行总结与分析。

1 系统模型及建模

1.1 系统模型

图1为系统模型。考虑在战场复杂环境中，有1个智能干扰机和1对通信用户（通信用户包括1个发射机和1个接收机），通信用户可以利用雷达探测装置对干扰机进行侦察定位，定位后利用相关技术减弱干扰。用户通信功率恒定为Pu。干扰机和用户可用频率范围相同，均匀分成M个可用信道，信道集定义为 M={1,2,…,M}。干扰机和通信用户在每个时隙均选择一个工作信道，可用信道带宽恒定为B。考虑信道历经块衰落，信道背景噪声为高斯白噪声。干扰机有j个功率发射等级，功率集定义为 P={P1,P2,…,Pj}。系统采用时分多址方式接入。

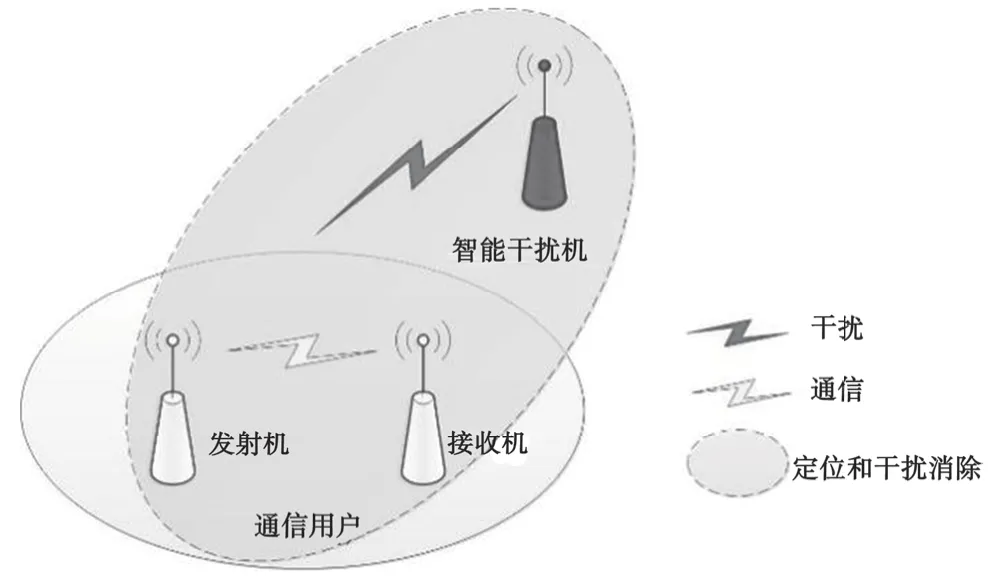
图1 干扰模型

通信用户进行周期跳频通信的同时会接收干扰机能量值（Received Signal Strength Indication，RSS）对干扰机进行定位[20-21]，且定位后采取有效措施减弱通信干扰，最大化保障己方信息传输。文献[22-24]中，通信用户会检测干扰机发出的能量值，不同的接收能量值对应不同的检测概率，一旦成功检测到能量就可以进行准确定位。在本文中将检测概率对应于定位概率。通信用户接收到的信噪比公式表示如下[21]：

其中，β代表干扰机到通信用户探测装置路径损耗系数，μj为信道瞬时衰落因子，p(j)为干扰机的干扰功率，d为干扰机到探测装置的距离，σ2代表零均值高斯白噪声的方差。干扰机功率越大，用户接收到的信号值越大。

用户探测装置的定位概率如下[22-23]：

PFA为探测装置的虚警概率，与探测装置自身性能有关[24]。文献[25]可以使探测装置的虚警概率达到10-4，因此根据式（25）在可以给定虚警概率时计算出干扰机定位概率Pra(j)。同时，本文在后面的工作中也仿真了不同虚警概率下不同信噪比对应的定位检测概率。根据以上检测方式和文献数据，干扰机不同的干扰功率对应的被定位概率集可以经过计算后得到：

干扰机工作时会根据自身干扰策略在每个时隙选择一个干扰信道fj和干扰功率pj，在最大化降低用户吞吐量的同时减小被定位概率。干扰机侦察装置可以获取通信方位置和距离，并通过干扰机接收到的通信方发射机能量与所提信道模型结合估算发射机功率，利用信道模型最后计算出用户接收机端的干信比（Jamming-plus-Noise-to-Signal-Ratio，JNSR）来调整自身干扰策略。干信比代表了信道中干扰信号的强度大小。

信号在传输过程中会发生路径损耗[26]。假设信号传输历经快衰落，设定系统工作时信道增益在当前时隙保持不变，在下一个时隙改变。gj表示干扰机到用户接收机的链路增益，定义如下：

其中，lj表示干扰机到用户接收机的距离，β表示干扰路径衰落系数，μj表示干扰机到通信用户接收机的瞬时衰落因子。同理，可得用户发射机到接收机的链路增益为：

其中，lu表示用户发射机到接收机的距离，α表示通信传输路径衰落系数，μu表示用户发射机到接收机的瞬时衰落因子。

用户接收到的信干噪比（Signal-to-Jammingplus-Noise-Ratio，SINR）定义如下[27]：

其中，N0代表信道背景高斯白噪声的功率，N0=B*σ2。pu代表用户恒定功率，Pj(i)代表干扰机选择的发射功率，θ(fj,fu)代表干扰机是否成功干扰通信信道。若fj=fu，则θ(fj,fu)=1，表示用户通信信道被成功干扰；若fj≠fu，则θ(fj,fu)=0，表示用户通信信道未受到干扰。

JNSR可P表示为[28]：

其中，N0表示信道背景噪声功率，RTR表示通信用户发射机到接收机的距离，RJR表示干扰机到通信用户接收机的距离。

1.2 问题建模

通信系统进行扫频通信，Tu代表用户通信信道。图2中横轴代表不同时隙，纵轴代表不同信道，空白信道代表信道未被占用。当干扰信道准确干扰到通信信道，表明干扰成功。干扰机根据自身干扰决策在每个时隙选择1个干扰信道和1个干扰功率等级进行干扰，如图2中Tj所示，且干扰机具有不同功率等级。在实际通信场景中，设定通信信道M=4，干扰机功率等级P=3，策略空间 Ω=M×P。

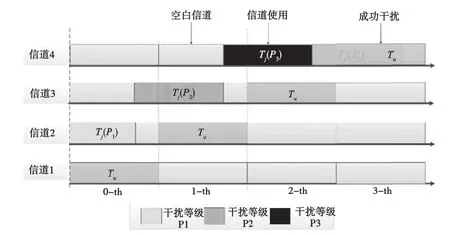
图2 系统传输时隙

动态变化环境中的信道衰落特性被建模成正态衰落模型[29]，信道增益可以表示为et，t表示零均值的高斯白噪声且方差为σ2。动态衰落通常用分贝表示，σ=0.1log(10)σdB，σdB为信道衰落值，通常取值在4～12 dB。在本文仿真中，信道衰落值设为10 dB。通信用户会按照设定规则切换信道进行通信。在时隙k干扰机选择的功率与信道联合策略为ak，定义通信用户在k时隙的吞吐量如下：

定义干扰机的效用为：

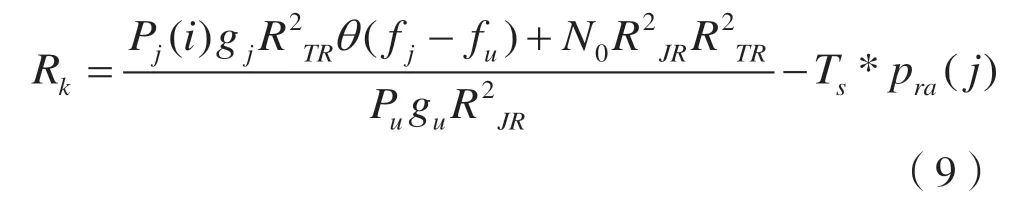
TS代表转换因子，一方面保证量纲的一致性，另一方面可以调整被定位概率的影响大小；pra(j)代表选择功率p(j)时所对应的被定位的概率，由式（2）计算得到。

1.2.1 马尔科夫决策过程

文中干扰决策的核心问题是动态环境中联合干扰决策问题。而动态未知环境下的干扰策略选择通常被建模为马尔科夫决策过程（Markov Decision Process，MDP）[30]。因此，本文功率与信道联合选择策略建模成为一个MDP问题，干扰机通过求解MDP寻找最优的干扰策略。MDP一般通过一个四元组定义为{S,A,P,R}[31-32]，S表示状态空间，A表示动作空间，P表示状态转移概率，R表示奖励值。其中，核心元素在本文中定义如下。

定义状态空间S。Sk∈S：S=[S1,S2,…,Sk]，Sk=(fu(k),fj(k),pj(k))表示在k时隙用户状态，fu(k)表示当前通信所在信道，fi(k)表示当前干扰信道，pj(k)表示当前干扰功率。

定义动作空间A。ak∈A：A=[a1,a2,…,ak]，其中ak=[(fj(k+1),pj(k+1)]，fj(k+1)∈M，pj(k+1)∈P表示在时隙k做出的动作，fj(k+1)表示k+1时隙的干扰信道，pj(k+1)表示k+1时隙的干扰功率。

定义状态转移概率矩阵P。P={p(Sk+1)|Sk,ak},Sk+1,Sk∈S表示从状态Sk选择动作ak到达状态Sk+1的概率。

定义奖励值R。R(Sk,ak)表示在当前状态Sk下选择动作ak得到的即时奖励值。在本文中定义Rk为式（9）。

本文中干扰机的目标是找到最佳干扰功率和信道，以最小化用户吞吐量并降低自身被定位的概率。干扰机的优化目标是使累积的奖励值最大化，优化目标定义如下：

1.2.2 Q学习算法

根据文献[33]，在状态Sk下最优策略π*的长期累积奖励值定义为：

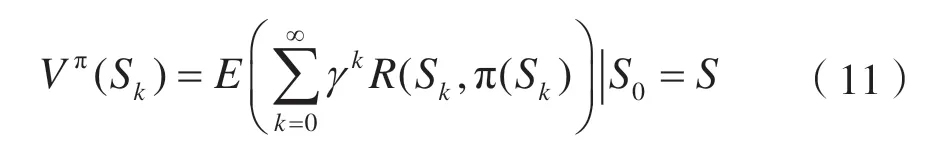
其中，γ代表时间折扣因子，表示在未来获得的奖励值对当前动作选取的重要程度。根据贝尔曼准则，式（11）的最大值为：

其中，R(Sk,a)为R(Sk,ak)的数学期望，PSk,Sk+1(a)代表在状态Sk下执行动作a到状态Sk+1的转移概率。将每个Q值和累计奖励值等价起来得到：

可以推导得：

强化学习正是通过和环境的交互不断强化对环境的认知，做出最佳干扰决策，因此被广泛用于求解马尔科夫决策模型。Q学习作为最有效的强化学习算法，一直被广泛使用。在系统模型中，状态转移概率未知时，Q学习可以通过求解MDP模型进行Q值迭代找到最优策略π*，Q值大小直接反映了动作的好坏。

Q学习中主要有两种动作更新策略，即贪婪（ε-greedy）策略[34]和玻尔兹曼（Boltzmann）概率策略[35]。玻尔兹曼更新策略在处理离散策略时具有优势，因此本文采用玻尔兹曼更新策略，策略选择向量Z(k)={z1(k),z2(k),…,zm(k)}，更新公式为：

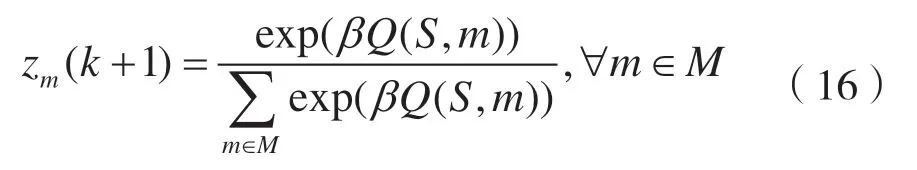
β表示玻尔兹曼更新系数，pm(k+1)表示在k+1时隙选择动作m的概率。Q值越大，被选中的概率越大。

根据文献[35]，Q值表的更新公式为：

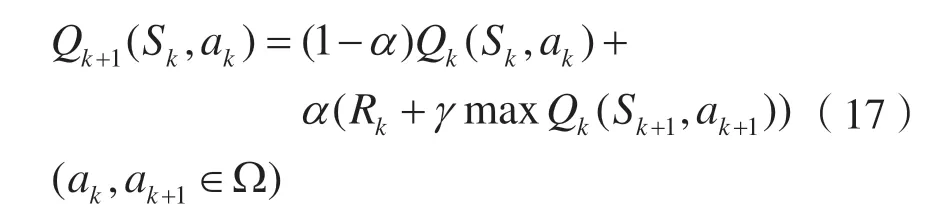
式中：其中α(0＜α≤1)表示学习更新步长，用来调整新状态和瞬时回报值对Q值的影响；γ(0＜γ≤1)表示折扣因子，即未来回报对当前选择动作的影响程度。Rk代表在状态Sk下采取动作获取的即时奖励值。干扰机根据Q值表在状态Sk下执行动作ak后到达状态Sk+1。

2 多域智能干扰算法

联合决策过程中的干扰-用户时隙图，如图3所示。在单个时隙内，Tj代表干扰时长，TWSS代表频谱感知时长，TL代表策略学习更新时长，Tu代表用户通信时长，{Tj+TWSS+TL}代表单个干扰时隙。在一个单独时隙内，干扰机按照干扰、感知和策略学习更新的顺序进行工作。

图3 干扰-用户时隙示意

干扰阶段：初始阶段，干扰机随机选择一个干扰信道fj(0)和功率等级pj(0)，即干扰机在0-th时隙开始以功率pj(0)在信道fj(0)上进行干扰；后续干扰策略由玻尔兹曼更新策略决策得到。

频谱感知阶段：在TWSS内，干扰机会通过宽带感知探测当前时刻各信道频谱状态，在k-th时隙感知到用户通信信道为fu(k)，则当前的状态为Sk(fu(k),fj(k),pj(k))，并计算当前时隙的奖励值Rk。

策略学习更新阶段：干扰机通过当前时隙获得的奖励值更新Q值表，并且根据更新后的Q值表通过玻尔兹曼更新策略决策出下一时隙的干扰信道。干扰机在之后每一个时隙都经历相同的决策过程，并不断更新Q值表。通过不断训练Q值表强化对环境的认知，最终在复杂动态变化的环境下干扰机可以决策出最佳干扰策略。本文提出的信道与功率联合干扰决策算法如表1所示。

3 仿真分析

图4给出了定位检测概率曲线图，在理论上分析了不同的虚警概率PFA条件下为达到某个检测概率Pra需要的接收能量大小。由图4可得，在给定虚警概率时，接收到的能量值越大，成功检测的概率就越大。

表1 基于强化学习的功率与信道联合干扰算法

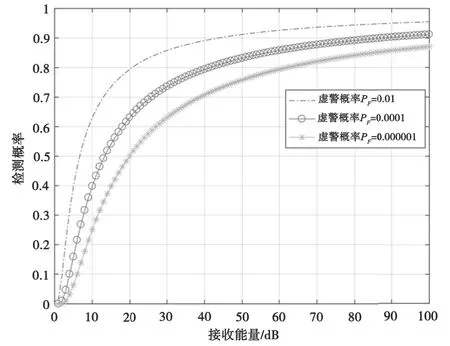
图4 检测概率变化曲线

本文主要研究如何在动态变化环境中利用强化学习找到最佳干扰策略，在保证干扰效果的同时降低干扰机被定位概率，并对所提算法的干扰性能进行了仿真分析，同时提出了随机干扰算法和基于Q学习的不考虑定位因素干扰算法。与所提学习算法进行对比，它能够更加直观反映所提干扰算法的干扰效果。随机干扰算法在每一个时隙通过随机选择干扰信道和功率进行干扰。基于Q学习的不考虑定位因素干扰算法是干扰机以恒定功率进行干扰，目标是使通信用户吞吐量降到最低。针对以上不同算法，仿真分析不同参数下的干扰性能。本文中干扰机功率等级设定为P={10 W,20W,40W}，在仿真通信环境中计算出被定位概率为Pra={0.1,0.2,0.5}。算法仿真中具体参数设置如表2所示，相关参数设置是参考文献和工作实际所得（所有仿真图数据为每50个点取平均）。

表2 相关参数设置

图5给出了所提算法效用函数变化曲线。在算法初期，干扰机效用很低，随着学习和训练的时间不断加长，干扰机逐渐掌握环境变化规律，效用值不断增加，最后收敛。

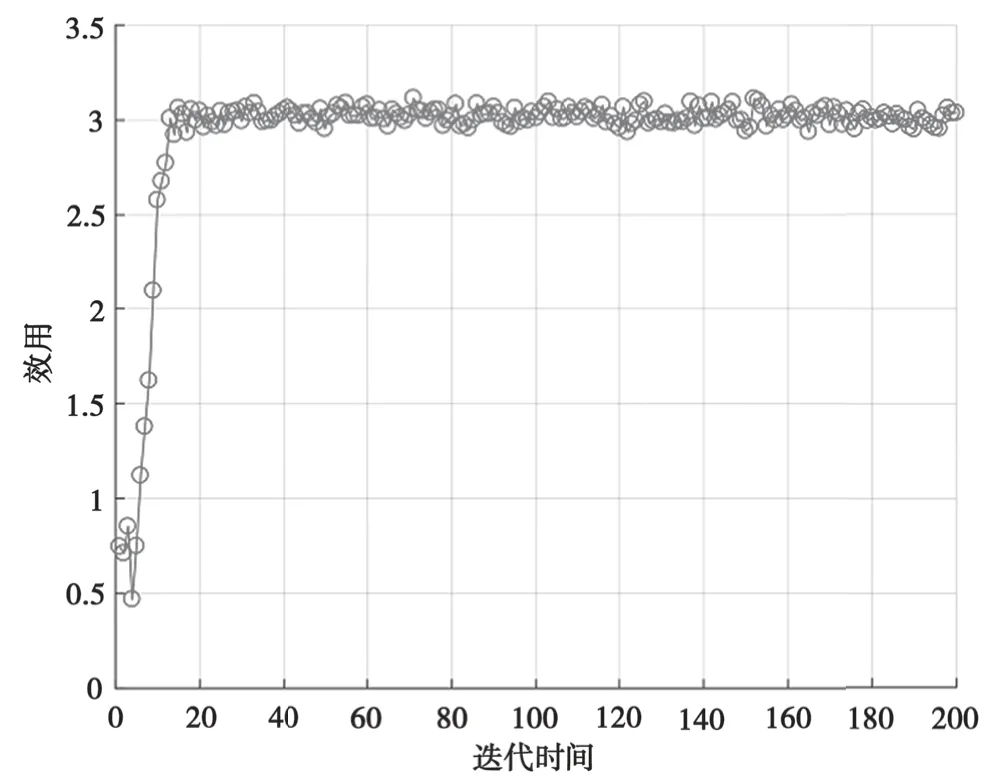
图5 效用函数变化曲线

图6给出了在用户状态S(fu(k)=1)（即用户在通信信道1传输数据）下干扰机各个动作选择概率曲线。仿真结果表明，在算法执行初期，用户在该状态下每个动作的选择概率相等。在经过一定时间的训练后，干扰机和环境不断交互，对环境认知逐渐加强，趋向于选择当前最优的干扰策略。从图6可以看出，经过一定时间训练后算法收敛，干扰机在用户状态S(fu(k)=1)下以近乎于1的概率选择发射功率p2=20 W、干扰信道为3的干扰动作。

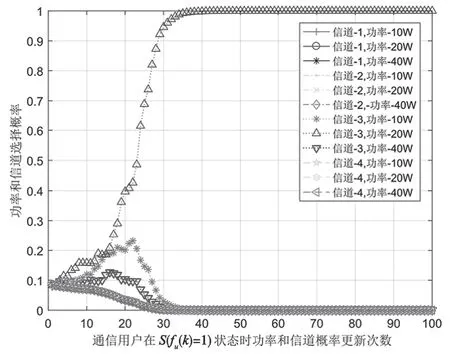
图6 各动作选择概率变化曲线

图7给出在用户状态S(fu(k)=1)下的各个动作的Q值变化曲线。在干扰算法运行开始，干扰机在每个动作下的Q值均为0。经过一定时间训练后，干扰机逐渐掌握环境变化规律，趋向于选择最优干扰决策。从图7可以看出，在训练后期算法收敛时，发射功率p2=20 W、干扰信道为3的联合干扰动作的Q值达到最大。因此，干扰机在所给状态下会持续选择发射功率p2=20 W，干扰信道为3的最优干扰策略。

图7 各动作Q值变化曲线

图8给出了所提算法和随机干扰算法的对比，方框线代表本文所提算法，圆点线代表随机选择干扰算法。从图8（a）可以看出，随机选择干扰算法吞吐量变化不定且无法收敛，用户平均吞吐量在0.75 Mb/s左右，表明随机算法并没有干扰到用户。而所提算法在初期的系统吞吐量和随机选择算法大概一致，然而随着训练时间的不断加长，干扰机掌握环境变化规律找到最佳干扰策略，用户吞吐量逐渐降低，最后算法收敛时的平均吞吐量达到0.1 Mb/s，用户吞吐量性能降低了约85%。图8中（b）给出了不同算法下干扰机被定位的概率值，可以看出，在干扰初期两种算法中干扰机被定位概率几乎相同，但是随着时间的增加，随机干扰无法收敛，一直处于波动中，但是本文所提干扰算法被定位概率逐步下降，最后收敛到0.2。和随机干扰算法相比，被定位概率平均降低了30%。以上结果表明，所提干扰算法具有更好的干扰效果。

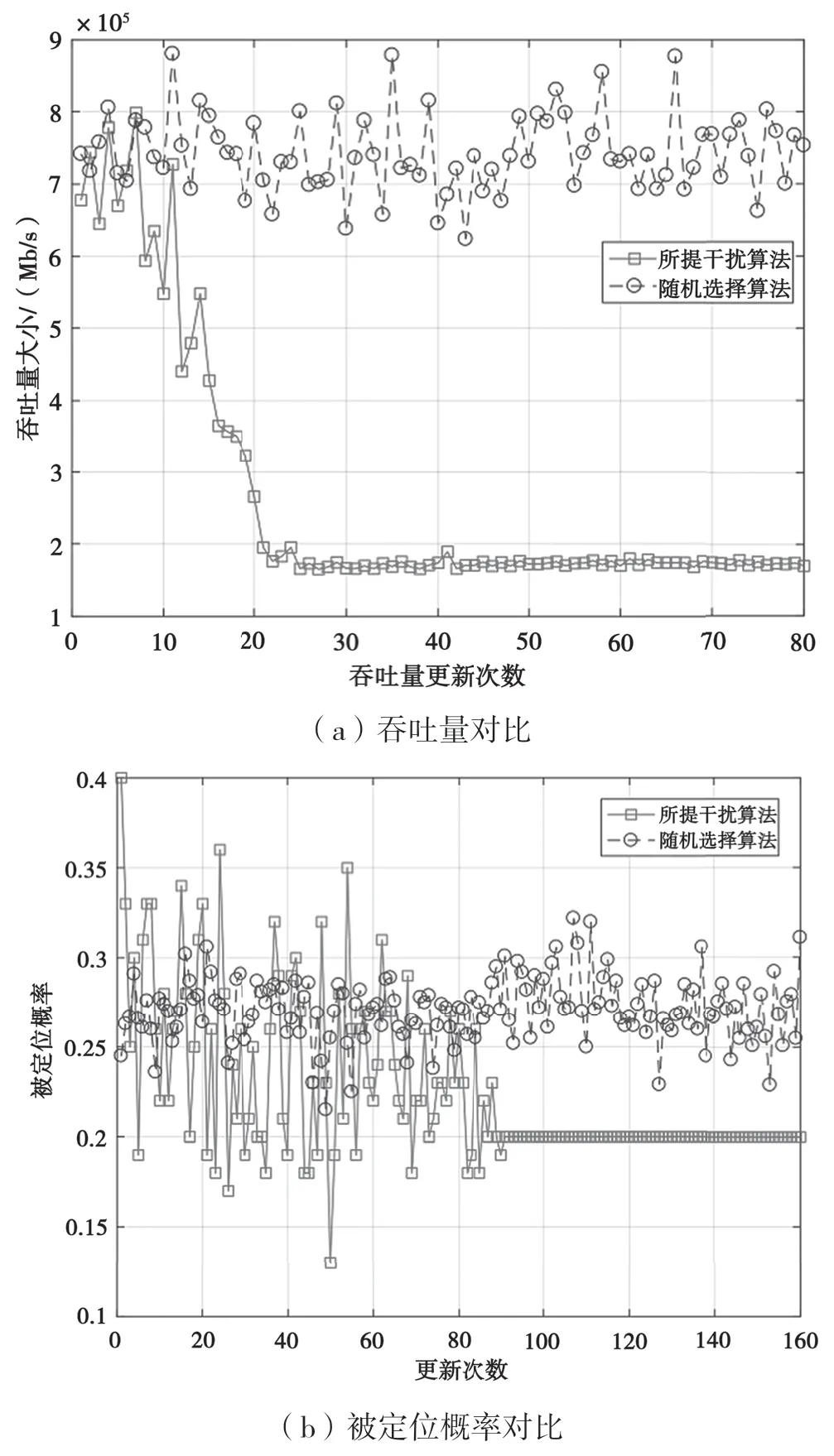
图8 所提算法和随机干扰算法对比

图9中，将所提算法和基于学习的不考虑定位因素干扰算法进行对比，对比算法干扰功率保持恒定，目标是最大化降低通信用户吞吐量，因此功率取最大发射功率。方框线代表本文所提算法，五角星线代表基于学习的不考虑定位算法。在图9（a）中可以看到，对比算法干扰功率保持最大且恒定时，通信用户吞吐量降低并不十分明显；但是，在图9（b）中所提智能干扰算法却可以使干扰机被定位概率降低60%。因此，本文设计的智能干扰算法具有更好的综合干扰效果。

图9 所提算法和基于Q学习不考虑定位干扰算法对比

4 结语

针对复杂电磁环境中单一域干扰效率不高且考虑到干扰机被定位的问题，首先将干扰机和通信用户之间的交互行为建模为一个马尔科夫决策过程，同时基于强化学习提出了联合干扰算法。仿真结果表明，所提算法可以通过和环境的不断交互探索到最佳干扰策略，在显著降低用户吞吐量的同时，降低干扰机被定位和发现概率。下一步考虑将所提算法应用到实际干扰系统中，搭建智能干扰平台对算法进行实际通信环境的验证。