基于改进灰色模型GM(1,1)的生活用水量预测研究

袁 旦，刘 献，张小丽

（华北水利水电大学水利学院，河南 郑州 450046）

1 研究背景

随着中国城市化进程的速度加快、经济水平的快速增长，全国居民用水量呈现不断增长的趋势。生活用水是区域生产活动用水的重要组成部分，需水量的预测作为供水决策、投资的重要参考指标，是制定供水和排水规划以及国民经济计划的基础和依据，在水资源规划和管理中起着非常重要的作用，对城市现代化建设具有重要的意义[1]。

目前，由于生活用水量受到包括人口、水价、经济发展等多个因素的综合影响，是一个非线性变化过程。很多学者对城市的生活用水量预测做了一些研究。李靖[2]等建立了用于城市用水量长期预测的小波神经网络耦合模型，并利用此模型对昆明市年用水量进行预测。结果表明，该模型应用于城市用水量的长期预测具有较高的预测精度和良好的推广能力。梁学玉[3]等基于灰色预测理论，建立了残差灰色预测模型与等维递补预测模型两者相结合的组合灰色预测模型，并应用于青海省西宁市用水量预测，结果表明组合模型的预测精度高于单一模型的预测精度。李黎武[4]等基于支持向量机（SVM）和小波框架理论,建立了城市用水量非线性组合预测模型，并采用SMO算法对模型进行求解，结果表明该模型具有很强的泛化能力与适应数据和函数变化的能力,能够有效提高预测精度,可用于供水系统调度的用水量预测。针对这个问题，本文采用背景值改进的灰色预测模型对河南省居民生活用水量进行预测，并与传统灰色预测模型进行对比，寻找改进模型的优点，以期通过本文研究，能够更好地预测生活用水量。

2 研究区概况

河南省域总面积16.7万km2，东接安徽、山东，北界河北、山西，西连山西，南临湖北，是全国重要的综合交通枢纽和人流物流信息流中心。河南省下辖17个地级市、一个省直辖县级市，21个县级市，83个县，53个市辖区。河南省作为全国人口大省，2018年常住人口9605万，地区生产总值为48055.86亿元，第一、二、三产业占比分别为8.1%、39.3%、52.6%，GDP增速为7.6%。2018年全省水资源总量339.8亿m3，人均水资源量为354.62 m3，人均水资源量不足全国人均水资源量的五分之一（2018年全国人均水资源量为1971.85 m3/人），远低于国际公认的人均500 m3的“极度缺水标准”，为典型的水资源严重短缺地区，严重影响着居民生活水平的提高，同时也严重阻碍着当地经济的发展。

3 研究方法

3.1 传统GM(1.1)预测模型

灰色系统理论由我国学者邓聚龙教授于1982年首次提出[5]，是一种用于研究数据少、信息量少的不确定性问题的理论方法。灰色预测是灰色系统理论的重要组成部分，而又尤以GM（1,1）为其常见模型。该模型通过对原始数据的累加生成，采用最小二乘法对其累加生成进行拟合，再进行累减处理，得到原始序列的预测值。

设已知参考数据列为x(0)=（x(0)（1），x(0)（2），…，x(0)（n）），做一次累加AGO生成数列：

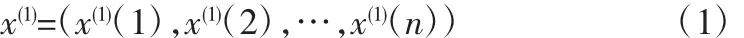
式中：x(1)（k）=∑x(0)（i）（k=1，2，…，n）。

将累加生成的数列，按每两个相邻数据求平均值的方法，得到其均值数列：

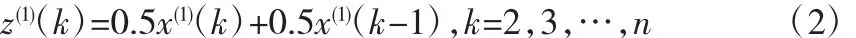
于是建立灰微分方程：

相应的白化微分方程：

式中：x(0)（k）称为灰导数；a称为发展系数；z(1)（k）称为白化背景值；b称为灰作用量。

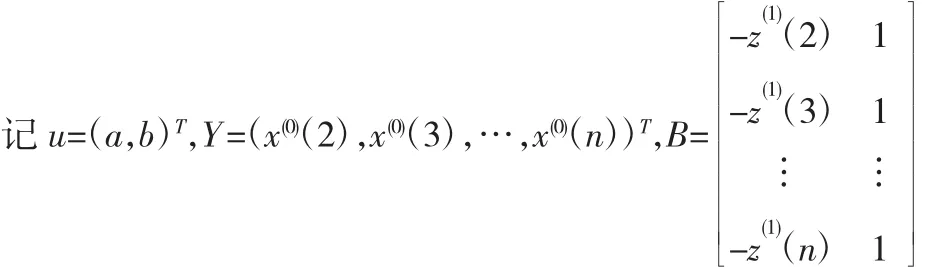
由最小二乘法并求式（4）得：

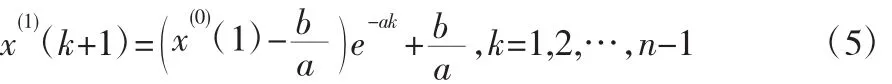
经累减还原可得原数据序列的估计值：

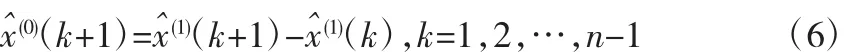
即：

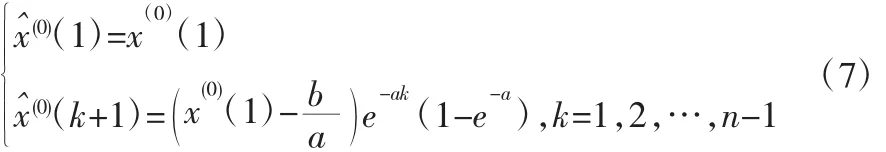
3.2 改进背景值的灰色预测模型

传统灰色模型的实质是，如果x(0)系列数据点的值均大于0，将数据系列累加生成后能在很大程度上消除数据的波动性，形状近似为指数函数；并用指数函数拟合，延展该拟合函数，再经过累减还原处理便可得到原始数据的预测值。

但在式（2）中，在定义背景值时认为在Δt=1的很短时间内，x（t）→x（t+Δt）不会发生突变，因此取它们的平均值为背景值，但是在实际应用过程中不可避免的会出现突变的情况，因此传统灰色预测模型的背景值赋值并不是很合理[6]。而由于灰色预测模型的拟合效果主要由背景值决定，这就为传统的灰色预测模型加入了更多的误差。

王钟羡等[7]认为背景值的构造用曲边梯形面积更加合理，采用积分法重构背景值，理论推导如下：

前提条件与传统模型一致，将式（2）在区间[k，k+1]上积分，有：

当设z(1)（k+1）为在区间[k，k+1]上的背景值时，则有：

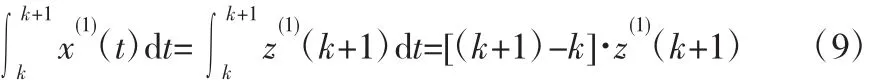
此背景值即为x(1)（t）在区间[k，k+1]上的定积分。

用如下指数函数曲线近似表示：

假设该曲线过x(1)（t）=cebt和x(1)（k），则：

由式（11）、式（12）可得：

推出背景值为：

即：

式(16)即为改进后背景值的取值。之后，根据灰色模型预测的方法，经过累减还原便可得到x(0)（k）的估计值：

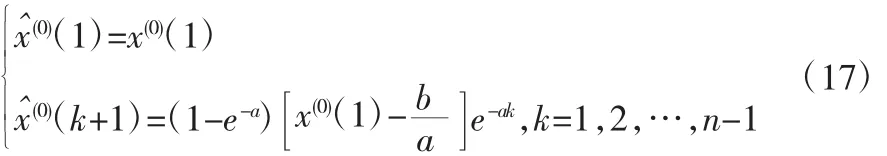
3.3 精度评价方法

灰色预测模型检验一般有残差检验、关联度检验和后验方差检验。本文采用后验方差检验，即通过均方差比值C和小误差概率P共同评定[8～9]。步骤如下：

（1）计算原始数据的平均值和方差：

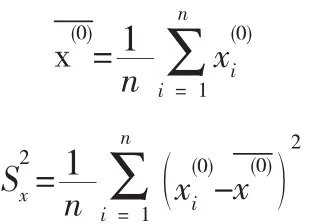
（2）计算残差均值和残差方差:

（3）计算后验方差比值C和最小概率误差P的值：

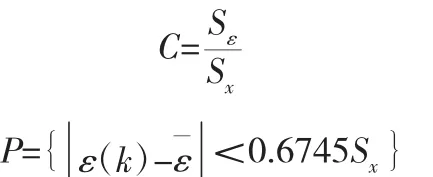
（4）根据C和P的值，对照灰色预测模型精度等级表来确定该模型精度，见表1。

表1 后验方差检验标准指数

4 应用实例

河南省2012年～2018年居民生活用水量数据（《国家统计年鉴》）见表 2。

表2 河南省2012年～2018年居民生活用水量

利用Matlab软件运行程序求解，由传统灰色预测模型，求解得其发展指数a=－0.04643，灰色作用量b=30.5665，所得到的原始数据估计值表达式为：

由改进背景值的灰色预测模型，求解得其发展指数a=－0.04612，灰色作用量b=30.6560，所得到的原始数据估计值表达式为：

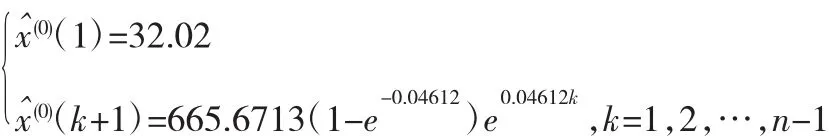
两个模型的计算结果见表3。

表3 两种模型用水量预测对比

参照表1后验方差检验标准判断两个模型的准确性，结果表明，传统灰色预测模型和背景值改进后灰色预测模型的模型预测精度等级均为优。但改进后的灰色预测模型所得到的模拟数据均方差比值C比传统灰色预测模型所得到的模拟数据均方差比值C更小，平均相对误差也小于传统灰色预测模型所得值。这说明，改进后的模型具有更高的拟合精度，拟合效果更好，可以更好的用来预测城市居民生活用水量。

由此，利用改进背景值的灰色预测模型对河南省2019年～2021年居民生活用水进行预测，预测结果见表4。

表4 2019年～2021年河南省居民生活用水量预测

从表4中可以看出，河南省2018年～2021年生活用水将继续保持增长。因此，政府应继续加强节水型社会的建设。本文就生活用水提出如下建议：完善生活用水监督机制，建立符合河南省实际情况的水资源管理体系；建立完备、统一的水价制度，充分利用水价的杠杆作用，制约随意取水及浪费水资源的行为；加强科技创新，改进全省水资源循环处理技术，提高城市生活用水回收率；加强节水教育和宣传，提高全民节水意识。

5 结论

基于改进背景值的灰色预测模型运用于生活用水需求量的预测。通过实例分析，该模型精度高于传统灰色预测模型。理论上，传统灰色预测模型背景值赋值不合理的缺陷在高增长序列中会表现得更为突出，改进背景值后的灰色模型能够更好地拟合原始数据序列。本文研究的河南省居民生活用水数据时间序列尽管不是高增长数据序列，但仍然验证了背景值改进后的模型能够取得更好的拟合效果，因而，将改进背景值的灰色预测模型运用到生活用水需求量是合适的。